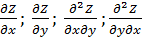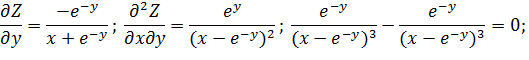Частные производные и дифференциалы высших порядков
Пусть имеем функцию двух переменных Z=f(x, y) частные производные Z’x и Z’y, вообще говоря, являются функциями от x и y, поэтому от низ можно снова находить частные производные. Частных производных второго порядка будет четыре, т.к.
Производные 2-го порядка можно снова дифференцировать как по x так и по y. Производных третьего порядка восемь:
Пример 1. Вычислить частные производные второго порядка от функции Z=ex ln y +sin y ln x
Теорема: Если функция Z=f(x, y) и ее частные производные определены и непрерывны в точке М(х, y) и в некоторой ее окрестности, то в этой точке Пример 2 Дана функция z= ln (x+e-y) Показать, что
|
каждую можно продифференцировать как по x так и по y. Вторые производные обозначаются так:
