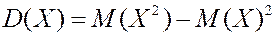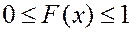Элементы комбинаторики
Размещения: Пусть из множества
ПРИМЕР: Сколькими способами можно набрать семизначный номер телефона, если все цифры разные?
Перестановка – произвольная упорядоченная запись
Выпишем перестановки из трех элементов.
ПРИМЕР: Сколькими способами можно разместить четверых гостей и хозяина за столом?
Сочетания. Пусть из множества
ПРИМЕР: Сколькими способами можно из 20 присяжных отобрать трех для участия в судебном процессе?
Алгебра событий. Пространством элементарных событий Суммой
ПРИМЕР. При подбрасывании игрального кубика событие
События ПРИМЕР. При подбрасывании игрального кубика событие ТЕОРЕМА. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
ПРИМЕР. В урне находятся 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, случайным образом извлеченный из урны, будет цветным (не белым)? Пусть событие событие
Событие Так как события
Произведением
ПРИМЕР. При подбрасывании игрального кубика событие
Событие
ПРИМЕР. При подбрасывании игрального кубика событие ТЕОРЕМА. Сумма вероятностей противоположных событий равна единице.
ПРИМЕР. Если вероятность попадания в цель при одном выстреле
ЗАДАЧА. При проверке качества деталей, выпущенных на заводе, в среднем из 100 деталей оказывается 85 деталей первого сорта и 10 деталей второго сорта. Найти вероятность того, что взятая наудачу деталь окажется бракованной.
Вероятности событий
Найдем вероятность того, что деталь бракованная.
ЗАДАЧА. Из 20 студентов группы 5 не сдали экзамен по математике, 4 – по информатике, причем 3 получили двойки по двум предметам. Какова вероятность, что случайно выбранный студент будет успевающим?
Вероятности событий
Тогда вероятность того, что случайно выбранный студент будет неуспевающим
Условная вероятность. Иногда необходимо определить вероятность случайного события Пусть множество
Условная вероятность события Если событие
ЗАДАЧА. Из 30 экзаменационных билетов студент знает 25. Если он отказался отвечать по первому билету, ему разрешают взять второй. Определить вероятность того, что второй билет ему известен. РЕШЕНИЕ. Пусть событие событие Если произошло событие
ТЕОРЕМА. Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого, при условии, что первое уже произошло.
Эта теорема может быть обобщена на любое число множителей.
ЗАДАЧА. Студент знает 25 из 30 экзаменационных вопросов. Экзамен сдан, если он ответит на три вопроса билета. РЕШЕНИЕ. Пусть событие
События
ТЕОРЕМА. Если события
ЗАДАЧА. Двумя стрелками производится по одному выстрелу по мишени. Вероятности попадания 0, 8 и 0, 9 соответственно. Найти вероятность того, что оба стрелка попадут в мишень. РЕШЕНИЕ. События
Формула полной вероятности. Система событий
Пусть событие ТЕОРЕМА. Вероятность события
ЗАДАЧА. В партии из 600 электрических лампочек 200 лампочек изготовлены на первом заводе, 250 на втором и 150 на третьем. Известны также вероятности 0.95, 0.91, 0.93 того, что лампочка окажется стандартного качества при изготовлении её соответственно первым, вторым и третьим заводами. Какова вероятность, что наудачу выбранная из данной партии лампочка окажется стандартной? РЕШЕНИЕ. Пусть событие Событие
Вероятности гипотез:
Условные вероятности события
Тогда полная вероятность события
Формула Байеса. Имеется полная группа несовместных гипотез По теореме умножения вероятностей имеем:
Отсюда следует, что
где ЗАДАЧА. Пусть при массовом производстве некоторого изделия вероятность того, что оно окажется стандартным, 0.95. Для контроля производится проверка стандартности, которая даёт положительный результат в 99% случаев для стандартных изделий и в 3% случаев для нестандартных. Какова вероятность стандартности изделия, выдержавшего проверку? РЕШЕНИЕ. Событие
Вероятности гипотез:
Условные вероятности события
Тогда полная вероятность события
Повторение опытов. Пусть производится серия испытаний. В результате каждого отдельного опыта событие А появляется с определенной вероятностью. Нас интересует число появлений события А в серии. Пусть опыты независимы и вероятность появления события А в каждом опыте постоянна. Схема Бернулли.
Поскольку вероятность Задача. Вероятность заболеть гриппом равна 0, 4. Найти наивероятнейшее число заболеваний гриппом из 5 сотрудников отдела. Решение.
Таким образом, с наибольшей вероятностью заболеет 2 сотрудника. Локальная теорема Муавра-Лапласа. Вычисление вероятности где Функция
ЗАДАЧА. Найти вероятность того, что событие РЕШЕНИЕ.
Сравним с точным значением
Интегральная формула Муавра-Лапласа. Если нас интересует вероятность того, что в серии из
где Здесь
ЗАДАЧА. Вероятность того, что зашедший в ресторан посетитель сделает заказ равна 0, 8. Определить вероятность того, что из 100 зашедших не менее 75 сделают заказ. РЕШЕНИЕ.
Закон редких явлений Пуассона. Если вероятность появления события
Закон Пуассона дает хорошее приближение при ЗАДАЧА. Завод отправил на базу партию в 500 изделий. Вероятность повреждения в пути 0, 002. Найти вероятность прибытия не более трех негодных изделий. РЕШЕНИЕ.
Случайные величины. Случайная величина – это величина, которая в результате опыта может принять то или иное значение случайным образом с некоторой вероятностью. Случайные величины могут быть дискретными и непрерывными. Дискретная случайная величина – это величина, число возможных значений которой конечно или счётно. Например, число попаданий при трех выстрелах(0, 1, 2, 3) или число вызовов, поступивших на телефонную станцию за сутки (0, 1, 2, 3, 4, …). Непрерывная случайная величина – величина, возможные значения которой непрерывно заполняют некоторый промежуток. Например, вес наугад взятого зерна пшеницы или скорость самолета в момент выхода на заданную высоту. Случайные величины обозначают Закон распределения случайной величины – это всякое соответствие, устанавливающее связь между значениями случайной величины и соответствующими вероятностями. Дискретные случайные величины. Рассмотрим дискретную случайную величину (ДСВ)
В результате опыта ДСВ
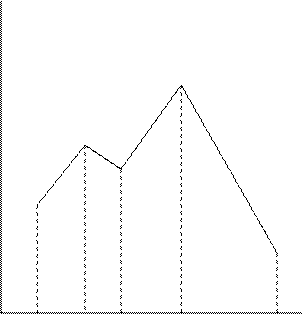
Простейшая форма задания значений случайной величины и соответствующих вероятностей – это таблица, которая называется ряд распределения ДСВ
Для наглядности можно по оси абсцисс отложить значения случайной величины, а по оси ординат соответствующие вероятности и соединить полученные точки.
ЗАДАЧА. Вероятность того, что необходимая студенту книга свободна 0, 7. Составить закон распределения числа библиотек, которые посетит студент, если всего в городе их четыре. РЕШЕНИЕ.
Числовые характеристики дискретных случайных величин. Математическое ожидание. Математическое ожидание ДСВ – число равное сумме произведений значений случайной величины на соответствующие вероятности.
Свойства математического ожидания. 1. Математическое ожидание от постоянной величины равно самой этой величине. 2. Математическое ожидание от мат. ожидания равно мат. ожиданию. 3. Постоянную можно вынести за знак математического ожидания. 4. Математическое ожидание суммы двух случайных величин равно сумме мат. ожиданий этих случайных величин. 5. Математическое ожидание произведения двух независимых величин равно произведению мат. ожиданий. ЗАДАЧА. Найти мат. ожидание суммы очков при подбрасывании двух игральных костей. РЕШЕНИЕ. Первый способ. Пусть
Второй способ. Пусть
Мода. Мода дискретной случайной величины – это то её значение, которому соответствует большая вероятность. В задаче ПРИМЕР.
Медиана. Медиана – то значение случ. величины, для которой выполняется условие: ПРИМЕР.
Дисперсия. Рассмотрим случайную величину (центрированная случайная величина). Для нее имеем:
Определение. Дисперсия сл. величины
Закон распределения
Для
Поэтому Свойства дисперсии. 1) Если 2) Для произвольной константы 3) Для суммы независимых случайных величин
4) Для произвольной с.в.
Пример. Найти дисперсию дискретной с.в., заданной законом распределения
Решение.
Если использовать вторую формулу, получим
Среднее квадратичное отклонение. Устраняет разницу в единицах измерения между математическим ожиданием и дисперсией.
Интегральная функция распределения вероятности. Пусть задана случайная величина
Свойства. 1. Значения интегральной функции удовлетворяют неравенству
|
элементов выбираются 
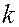элементов. Такая комбинация с учетом порядка записи и называется размещением. Число размещений определяется формулой
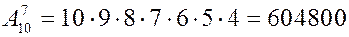
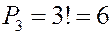
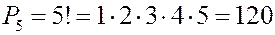
называется множество всех элементарных исходов, относящихся к заданному опыту.
( или объединением 
) двух событий называется событие, которому благоприятствуют исходы, благоприятствующие событиям 
или 
.
- выпала “4”; 
- выпала “6”.
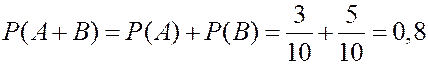
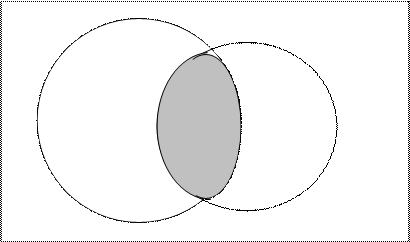
( или пересечением 
) двух событий называется событие, которому благоприятствуют исходы, благоприятствующие одновременно событиям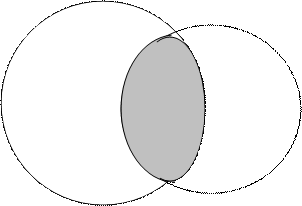 
называется противоположным событию 
благоприятствуют все те элементарные исходы, которые не являются благоприятствующими для события 
, то вероятность промаха
.
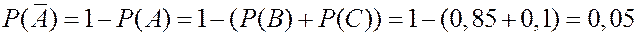ТЕОРЕМА. Если события 
известны
А нам необходимо найти вероятность противоположного события. Так как 
получим
состоит из 
исходов, событию 
благоприятствуют 
исходов. Тогда
или 
.
будет 
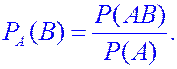
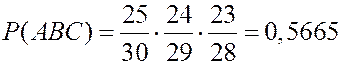
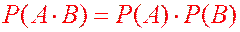
называется полной группой событий для данного испытания, если любым исходом опыта является одно и только одно событие этой группы. Таким образом, событие 
достоверно, то есть 
, и события 
и 
попарно несовместны, то есть 
.
.
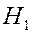
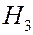
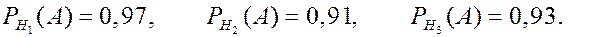
известны до опыта (априори). Производится опыт, в результате которого зарегистрировано появление события 
. Необходимо переоценить вероятности гипотез после опыта (апостериори), то есть нужно определить условные вероятности 
.
.
,
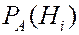находим по формуле полной вероятности.
.
представляется членами разложения бинома 
, то распределение называется биномиальным.
.
,
,
,
,
.
. Поэтому на практике применяют приближенные формулы. Одна из них формула Муавра-Лапласа. 
- четная: 
; достигает максимума 
в точке 
. При этом 
: 
.
.
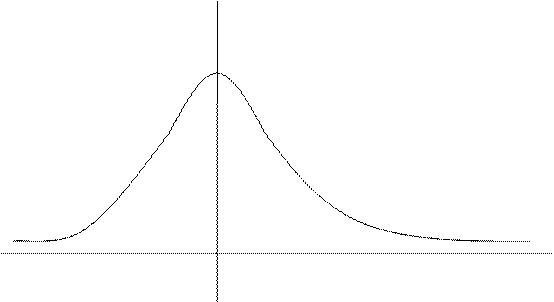
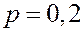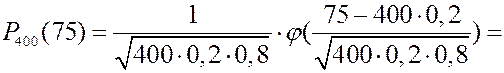
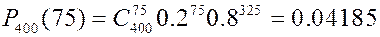и не более 
раз, то
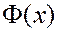- функция Лапласа. Функция 
. При возрастании 
функция 
, 
. Можно считать 
при всех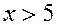 
.
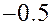
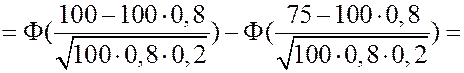
, а число испытаний велико 
, то для приближенного вычисления 
. Тогда
.
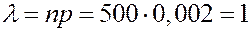
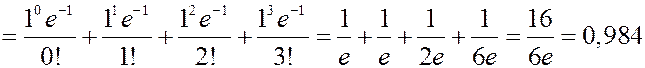Сравним с точным значением:
, а значения случайных величин 
.
с возможными значениями 
, 
, 
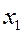
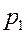
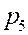
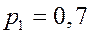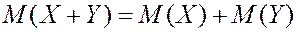
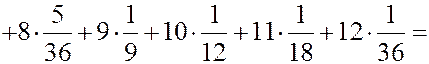
- число очков на первом игральном кубике,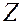 
- число очков на втором.
.
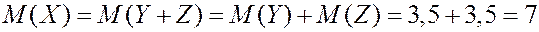
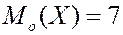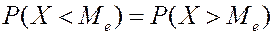
, то есть
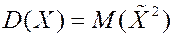Û 
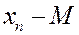
, следовательно, получаем
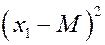
, то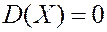 
:
