Формализация слабоструктурированных и неструктурированных задач экономикиСамый ответственный этап системного анализа – формирование проблемной ситуации. Полученное множество проблем (проблематика) является исходным пунктом для системного анализа. После определения проблемы следующим по важности этапом анализа становится выявление целей. Содержание процесса перехода от целей к критериям и многие особенности этого перехода становятся ясными, если рассматривать критерии как количественные модели качественных целей. В самом деле, сформированные критерии в дальнейшем в некотором смысле заменяют цели. От критериев требуется как можно большее сходство с целями, чтобы оптимизация по критериям соответствовала максимальному приближении. К цели. С другой стороны, критерии не могут полностью совпадать с целями уже хотя бы потому, что они фиксируются в различных шкалах: цели – в номинальных, критерии – в более сильных, допускающих упорядочение. Критерий – это подобие цели, ее аппроксимация, модель. Конкретнее, критерий является отображением ценностей (воплощенных в целях) на параметры альтернатив (допускающие упорядочение). Определение значения критерия для данной альтернативы является, по существу, косвенным измерением степени ее пригодности как средства достижения цели. Неопределенность целевой функции имеет место в случае невозможности представления цели системы в виде скалярной целевой функции. Выбор целевой функции является одной из самых трудных проблем при проведении системных исследований. Часто целевые функции оказываются противоречащими друг другу. Например, этот факт нашел выражения в распространенной целевой функции добиться максимума эффективности с минимумом затрат. При наличии нескольких целевых функций (в том числе и противоречивых) математика не может дать однозначного ответа, но она может помочь принять решение и сделать правильный выбор. В этом и будет заключаться решение проблемы неопределённости целевой функции. Неопределённости среды и системы вызваны дефицитом информации об их состояниях. В этом случае не могут быть получены конкретные характеристики среды и системы (в том числе и стохастические). Методы решения таких задач наименее разработаны. Поэтому исследование сложных систем опирается не только на обширный математический аппарат, но и на целый ряд методов преодоления неопределенностей. Для сравнения различных целей системы вводится функция некомфортности Каждое взаимодействие из множества 1) как взвешенную сумму где
2) по наиболее важнейшей целевой функции По уровню некомфортности Пусть отношение предпочтения по важности ля всех частных целевых функций 2. Выбор главной целевой функции при введении ограничений на остальные целевые функции. 3. Последовательная оптимизация по главной целевой функции с последующим введением уступок по другим наиболее важным целевым функциям. 4. Последовательная оптимизация по важности целевых функций с достижением по каждой требуемого значения. В первом случае наиболее важная целевая функция принимается за главную системы
где Для получения хорошего решения по менее важным целевым функциям на практике приходится делать уступки Этот подход реализуется в методе последовательных уступок (второй случай), который сводится к решению последовательности задач оптимизации:
где
В качестве компромиссного решения Эффективная точка в процессе решения экономической задачи многокритериальной оптимизации ищется в области компромиссов. Минимизация в области компромиссов векторного критерия означает, что нельзя больше уменьшать значение одного из частных критериев, не увеличивая значения хотя бы одного из остальных. Для определения экстремума в области компромиссов необходимо перейти от задачи векторной оптимизации к задаче нелинейной оптимизации со специально сконструированной скалярной целевой функцией. Процесс образования скалярной функции, являющейся обобщенной целевой функцией для задачи многокритериальной оптимизации, называется объединением (свертыванием) векторного критерия оптимальности. В зависимости от информации о важности («весе») частных целевых функций можно выделить следующие типы объединения: объединение количественно «взвешенных» целевых функции; объединение целевых функций, для которых указано отношение предпочтения по важности; объединение целевых функций при отсутствии информации об их важности. Целевые функции
где Весовые коэффициенты можно интерпретировать как субъективные вероятности. Под субъективной вероятностью понимается мера уверенности некоторого человека или группы людей в том, что данное событие в действительности будет иметь место. Субъективная вероятность получается в результате опроса эксперта или _пии_пы экспертов. Она находит применение в тех случаях, когда невозможно воспользоваться вероятность объективной. Этому может быть несколько причин: неполнота или отсутствие данных о наблюдении в прошлом, в частности, отсутствие аналогов исследуемой ситуации в прошлом, необоснованно высокая стоимость получения объективной вероятности, а также подозрение, сто ранее наблюдавшиеся закономерности и полученные объективные вероятности не будут иметь место в будущем. Как мера уверенности человека в возможности наступления событий субъективная вероятность может быть формально представлена различными способами: распределением вероятностей на множестве событий, бинарным отношением на множестве событий, не полностью заданным распределением вероятностей или частным бинарным отношением или другими способами. В зависимости от формы представления выделяют количественную и качественную субъективную вероятность. Количественная субъективная вероятность является вероятностной мерой на множестве событий, удовлетворяющей той же системе аксиом, что и вероятность объективная. Поэтому с формальной точки зрения количественная субъективная вероятность ничем не отличается от объективной вероятности. Разница заключается в том смысле, которой вкладывается в эти понятия. Практически построение количественной субъективной вероятности требует от эксперта указания числовых значений вероятности для ряда событий. Известно, однако, что такая количественная информация является для человека более сложной и потому ненадежной. Значительно более простой и потому более достоверной является информация, состоящая из ответов на вопросы о сравнительной вероятности (возможности) двух событий. В связи с этим большой практический интерес представляет нечисловая формализации субъективной вероятности, основанная на использовании отношений превосходства и равенств событий поверхности (функций некомфортности как мер качества цели). Аксиомы качественной вероятности выражают минимальные требования к последовательности и непротиворечивости субъективных суждений. Основным вопросом, связанным с понятием качественной вероятности, традиционно считается вопрос о возможности построения количественной вероятности, которая в каком-либо смысле согласована с качественной. Это явилось отражением того факта, что при решении практических задач до последнего времени использовалось только количественная вероятность, а качественная вероятность вызывала только теоретический интерес. Однако в последнее время в теории принятия решений появились специальные процедуры, рассчитанные на анализ качественной информации, в связи с чем понятие качественной вероятности приобрело самостоятельное практическое значение. Для получения количественных оценок субъективной вероятности разработано большое число методов. Однако практически все эти методы (метод отношений, метод собственного значения, метод равноценной корзины, метод переменного перевала, метод фиксированного интервала и др.) основаны на проведении опроса эксперта или группы экспертов. Поэтому представляется целесообразным при решении рассматриваемой проблемы использовать формализованные методы получения количественных оценок субъективной вероятности на основе теоретико-информационного подхода. Наличие ряда ситуаций, обладающих той или иной степенью неопределённости, требуют для своего описания привлечения математического аппарата, который бы априори включал в себя вероятность появления неопределённости и ее меры (энтропии Шеннона Опираясь на постулаты качественной вероятности (Финатти и Крупмана) для простого линейного отношения порядка приоритетов целевых функций используется так называемые оценки Фишборна Заметим, что помимо простого отношения порядка предпочтения имеет место и строгое отношение порядка для определения весовых коэффициентов используется зависимость
Для целевых функций, для которых может быть установлено усиленное линейное отношение порядка для учёта значимости целевых функций используется зависимость
В качестве показателя, характеризующего степень снижения уровня неопределённости, может быть использован показатель избыточности
характеризующий степень близости вероятностных оценок к равномерному закону распределения (максимальной неопределённости при многокритериальной схеме формирования целевой функции). Сущность метода парных сравнений заключается в наиболее общей постановке в нахождении результирующего критерия выбора по оценкам, даваемым экспертами, и по показателям, полученным в результате информационно-статистического анализа исследуемой системы. Статистические методы обработки исходной информации основаны на предположении, что полученные оценки в силу ряда причин являются случайными, законы распределения которых в общем случае неизвестны. Задача метода парных сравнений заключается в том, чтобы внести меньшую погрешность (минимум недостающей информации) при идентификации законов распределения, вводимых в рассмотрение оценок, сформировать модель расчёта весовых коэффициентов этих оценок и определить и рассчитать обобщенный критерий сравнения исследуемых объектов. В тестах проверки статистических гипотез о принадлежности малой выборки ( Так, например, для нормального закона распределения где
где Статистика критерия для минимального объёма выборки Если случайные величины
Таким образом, используя полученные законы распределения инвариантной статистики Аналогичным образом можно ввести в рассмотрение инвариантные статистики для выборки из других генеральных совокупностей. Для экспоненциального закона с функцией распределения
где Очевидно, что отношение этих случайных величин не зависит от параметра распределения Действительно, можно показать, что если случайные величины Аналогично можно внести в рассмотрение законы распределения инвариантных статистик из выборок однопараметрических законов распределений (Рэлея, одностороннего нормального, Максвелла, показательно-степенного и др.). Привлечение однопараметрических законов распределений обусловлено тем обстоятельство, что в методе парных сравнений рассматриваются две случайные величины (два параметра оценки эффективности (системы), имеющих стохастическую природу). Выбор предпочтительного закона распределения в этом случае представляется целесообразным производить на основе принципа стохастического доминирования введением Дальнейшим развитием идеи стохастического доминирования может служить использование экстремальных распределений экстремальных величин. Если при парном сравнении имеют место ряд качественных показателей (строгое ранжирование), допустим, что объект и наоборот объект то, используя принцип максимума неопределённости и меру
можно показать, что вероятностные меры по этим показателям имеют виз
Для этого достаточно решить следующую экстремальную задачу
В качестве модели расчёта весовых коэффициентов где Тогда обобщенные показатели сравнения можно определить следующим образом
где Согласно введенным обобщенным оценочным показателям Постановка оптимизационных задач обусловливает необходимость разработки эконометрических моделей элементов экономической структуры. Основу эконометрических моделей составляют два вида функциональных зависимостей: производственные функции и функции потребительского спроса. Производственная функция
С производственной функцией связаны вполне определенная экономическая интерпретация и некоторые показатели, используемые в экономическом анализе, прежде всего, это производительность труда и предельная производительность труда
Наиболее часто для квазистатического описания экономической динамики используются производственные функции с постоянной эластичностью замещения (CES-функции), имеющие вид
где Постоянству эластичности замещения (Constant Elasticity of Substitution – CES) соответствует условие
где
Производственная функция Кобба-Дугласа является предельным вариантом CES-функции (1) при где Для производственной функции Кобба-Дугласа эластичность замещения равна единице (основные фонды и трудовые ресурсы в одинаковой мере замещают друг друга). Вторым предельным вариантом CES-функции является функция с фиксированными пропорциями
Для производственной функции с фиксированными пропорциями эластичность замещения нулевая: основные фонды и трудовые ресурсы не могут замещать друг друга, а должны использоваться в заданной пропорции, избыток фондов или трудовых ресурсов не увеличивают выпуска, что соответствует неизменности рабочих режимов технологических процессов. Производственная функция Кобба-Дугласа и (в несколько меньшей степени) функция полезности Кобба-Дугласа стали традиционным средством анализа экономических вопросов. Однако их применение предлагает принятие довольно суровых ограничений. Например, требования гомотопической эквивалентности и единичной эластичности замены. Заметим, что общий вид гомотетичных производственных функций может быть записан как Регрессионный анализ является одним из наиболее распространенных методов обработки результатов наблюдений при изучении зависимостей в экономике и в других областях. Проблема регрессионного анализа в экономике характерна тем, что о распределениях изучаемых величин нет достаточной информации. Целью регрессионного _пиилиза является определение общего вида уравнения регрессии, построение статистических оценок неизвестных параметров, входящих в уравнение регрессии, и проверка статистических гипотез о коэффициентах регрессии. При изучении связи между двумя величинами по результатам наблюдений Если заданы
Коэффициенты линейной средней квадратической регрессии для генеральной совокупности определяются в результате минимизации функции
где
где
Прямая средней квадратической регрессии в этом случае имеет вид
Соответствующие коэффициенты регрессии для выборки могут быть записаны следующим образом
Достаточно рассмотреть выборочное распределение величины Выражение для плотности вероятности выборочного коэффициента регрессии
где Если ввести новую величину
то можно показать, что
в которой характеристики совокупности Используя распределение Стьюдента, можно поставить и решить задачу проверки статистических гипотез о равенстве единице или нулю Анализ задач распознавания явлений в случае, когда между признаками объектов и классами, к которым они могут быть отнесены, существуют вероятностные связи, показывает, что построение алгоритмов распознавания может быть основано на результатах теории статистических решений. Сущность такого подхода в теории распознавания образов заключается в следующем. Пусть совокупность объектов подразделена на классы Чтобы определить, к какому классу отнести объект вводят некоторое значение признака
|

 , которая является мерой качества цели. Эта функция позволяет сравнить две целевые функции
, которая является мерой качества цели. Эта функция позволяет сравнить две целевые функции  и
и  . Если целевая функция
. Если целевая функция  (
( , где
, где  – знак предпочтения), то
– знак предпочтения), то  . При
. При  цели эквивалентны, то есть
цели эквивалентны, то есть  ;
;  .
. может быть реализовано в системе, если мы поставим ему в соответствие целевую функции. Весомость различных _пии_вых функций (и взаимодействий) определяется через меру некомфортности, которую можно определить:
может быть реализовано в системе, если мы поставим ему в соответствие целевую функции. Весомость различных _пии_вых функций (и взаимодействий) определяется через меру некомфортности, которую можно определить: ,
,  ,
, – целесообразность постановки данной целевой функции;
– целесообразность постановки данной целевой функции; – вес данной целевой функции для выполнения глобальной цели системы;
– вес данной целевой функции для выполнения глобальной цели системы;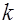 – число сформулированных целевых функций;
– число сформулированных целевых функций; ,
,  определяют необходимость включения данной целевой функции в логическое множество целей системы. Значения коэффициентов
определяют необходимость включения данной целевой функции в логическое множество целей системы. Значения коэффициентов  задано условием
задано условием  … Решение задачи может идти по следующим направлениям:
… Решение задачи может идти по следующим направлениям: и ее стремятся минимизировать при заданных «пороговых» значениях
и ее стремятся минимизировать при заданных «пороговых» значениях  остальных частных целевых функций:
остальных частных целевых функций: ,
,  ,
, ;
; 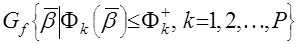 .
. по другим наиболее важным целевым функциям.
по другим наиболее важным целевым функциям. ,
,  ,
, 
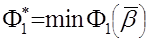 ,
, 
 ;
;  ;
; – оптимальное решение задачи для фиксированного
– оптимальное решение задачи для фиксированного 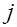 ;
; принимается вектор
принимается вектор  . Этот метод удобен тем, что для каждой
. Этот метод удобен тем, что для каждой  -й целевой функции приобретается выигрыш. В третьем случае каждый раз задача решается до обеспечения
-й целевой функции приобретается выигрыш. В третьем случае каждый раз задача решается до обеспечения  , где
, где  обеспечивает требуемое значение
обеспечивает требуемое значение  ,
,  будем считать количественно «взвешенными», если каждой из них можно поставить в соответствие некоторое число
будем считать количественно «взвешенными», если каждой из них можно поставить в соответствие некоторое число  , которое численно характеризует ее важность по сравнению с другими _пии_выми функциями. Параметры
, которое численно характеризует ее важность по сравнению с другими _пии_выми функциями. Параметры  называются весовыми коэффициентами. Это позволяет получить скалярную целевую функцию системы
называются весовыми коэффициентами. Это позволяет получить скалярную целевую функцию системы  путем образования суммы частных целевых функций, умноженных на свои весовые коэффициенты (метод взвешенных сумм)
путем образования суммы частных целевых функций, умноженных на свои весовые коэффициенты (метод взвешенных сумм) ,
, ,
,  .
. ).
). ,
, 
 ,
, ,
, 
 .
. ,
, 
 .
. ,
, и более) определенной генеральной совокупности в основном составляют инвариантные статистики, которые путем некоторых преобразований трансформируются к виду, обладающему свойством независимость от параметров распределения исходных случайных величин. Следует заметить, что универсальных преобразований подобного рода не существует, однако в каждом конкретном случае такое преобразование можно найти. В основе таких преобразований лежит переход от имеющихся выборочных наблюдений
и более) определенной генеральной совокупности в основном составляют инвариантные статистики, которые путем некоторых преобразований трансформируются к виду, обладающему свойством независимость от параметров распределения исходных случайных величин. Следует заметить, что универсальных преобразований подобного рода не существует, однако в каждом конкретном случае такое преобразование можно найти. В основе таких преобразований лежит переход от имеющихся выборочных наблюдений  случайной величины
случайной величины  к некоторым функциям от стандартных случайных величин и исключение мешающих с точки зрения математической статистики параметров распределении.
к некоторым функциям от стандартных случайных величин и исключение мешающих с точки зрения математической статистики параметров распределении. используя соотношения
используя соотношения  ,
,  ,
, – стандартная нормально распределенная случайная величина с параметрами
– стандартная нормально распределенная случайная величина с параметрами  и
и  , можно получить непараметрическое преобразование в виде
, можно получить непараметрическое преобразование в виде *,
*,  ,
, – вариационный ряд, составленный из исходной выборки наблюдений.
– вариационный ряд, составленный из исходной выборки наблюдений. распределена по закону (пусть
распределена по закону (пусть  ), тогда
), тогда 
 .
. взаимно независимы и распределены одинаково нормально и из них составлен вариационный ряд
взаимно независимы и распределены одинаково нормально и из них составлен вариационный ряд  ,
,  , то закон распределения статистики
, то закон распределения статистики  ,
,  , имеет вид
, имеет вид .
. , применяя преобразования Н.В. Смирнова (метод обратных функций), можно получить следующее представление случайных величины
, применяя преобразования Н.В. Смирнова (метод обратных функций), можно получить следующее представление случайных величины ,
,  ,
, – случайная величина, равномерно распределенная на интервале
– случайная величина, равномерно распределенная на интервале  .
. . Следовательно, для выборки случайных величин
. Следовательно, для выборки случайных величин  из генеральной совокупности с экспоненциальным законом распределения преобразование вида
из генеральной совокупности с экспоненциальным законом распределения преобразование вида  является инвариантным преобразованием выборочных _пии_мдений.
является инвариантным преобразованием выборочных _пии_мдений. взаимно независимы и распределены одинаково экспоненциально и если
взаимно независимы и распределены одинаково экспоненциально и если  ,
,  инвариантных к параметру экспоненциального закона, имеет вид
инвариантных к параметру экспоненциального закона, имеет вид  .
. – упорядочения рассматриваемых законов распределений.
– упорядочения рассматриваемых законов распределений. превосходит объект
превосходит объект  по
по 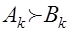 ,
, 
 показателям
показателям  ,
,
 и
и  .
. ,
,  .
. вводимых в рассмотрение показателей представляется целесообразным использовать энтропийную меру
вводимых в рассмотрение показателей представляется целесообразным использовать энтропийную меру  и зависимость
и зависимость  ,
, – общее число показателей (
– общее число показателей ( – число показателей, доминирующих для исследуемой системы,
– число показателей, доминирующих для исследуемой системы, 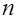 – число показателей, доминируемых для этой же системы).
– число показателей, доминируемых для этой же системы). ,
, ,
, ;
;  .
. и
и  оптимальным решением в методе парных сравнений систем
оптимальным решением в методе парных сравнений систем  (или
(или  ).
). выражает, какое количество продукта можно произвести за единицу времени, обладая капиталом
выражает, какое количество продукта можно произвести за единицу времени, обладая капиталом  и трудовыми ресурсами
и трудовыми ресурсами  . Понятие производственной функции неявно включает в себя некоторую оптимизацию. Величина
. Понятие производственной функции неявно включает в себя некоторую оптимизацию. Величина  , неотрицательны, положительно однородны первой степени
, неотрицательны, положительно однородны первой степени  , дважды непрерывно дифференцируемы, причем
, дважды непрерывно дифференцируемы, причем
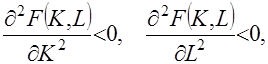
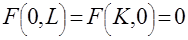 .
.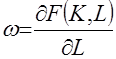 .
. , (1)
, (1) – константы.
– константы. , (2)
, (2)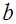 – коэффициент регрессии в линейной зависимости (в логарифмическом масштабе) производительности труда
– коэффициент регрессии в линейной зависимости (в логарифмическом масштабе) производительности труда  и предельной производительности труда
и предельной производительности труда 
 . (3)
. (3)
 , (4)
, (4) и
и 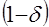 – коэффициенты эластичности, определяющие оптимальную пропорцию интенсивности затрат факторов
– коэффициенты эластичности, определяющие оптимальную пропорцию интенсивности затрат факторов  в зависимости (1)
в зависимости (1) (5)
(5) , где
, где  – функция, монотонная по
– функция, монотонная по  , а
, а  – функция первой степени однородности по
– функция первой степени однородности по  предполагается, что одна из них имеет некоторое распределение вероятностей при фиксированном значении другой. В общем случае результаты наблюдений
предполагается, что одна из них имеет некоторое распределение вероятностей при фиксированном значении другой. В общем случае результаты наблюдений 
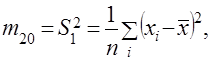

 (6)
(6) ,
, – оператор определения математического ожидания. Решение этой экстремальной задачи дает единственное решение
– оператор определения математического ожидания. Решение этой экстремальной задачи дает единственное решение , (7)
, (7) – коэффициент корреляции,
– коэффициент корреляции, ,
,  – средние значения величин
– средние значения величин  и
и  . (8)
. (8) ,
, 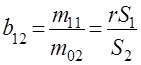 . (9)
. (9) (распределение для
(распределение для  получается с помощью перестановки индексов).
получается с помощью перестановки индексов). , (10)
, (10) – детерминант матрицы вторых моментов
– детерминант матрицы вторых моментов  .
. , (11)
, (11) распределено по закону Стьюдента с
распределено по закону Стьюдента с  степенью свободы. Плотность вероятности (4.10) содержит все три теоретических момента
степенью свободы. Плотность вероятности (4.10) содержит все три теоретических момента  и
и  и, если необходимо оценить гипотетическое (истинное) значение коэффициента регрессии
и, если необходимо оценить гипотетическое (истинное) значение коэффициента регрессии  , то представляется целесообразным рассмотреть величину
, то представляется целесообразным рассмотреть величину , (12)
, (12) и
и  и
и  , а множитель
, а множитель  заменен на
заменен на  . В этом случае статистика
. В этом случае статистика  (12) имеет распределение Стьюдента с
(12) имеет распределение Стьюдента с  степенями свободы.
степенями свободы. коэффициента регрессии в зависимости (3). Такое решение позволяет оценить с определенной долей вероятности предпочтительность предельных вариантов CES-функций: функции Кобба-Дугласа (4) или функции с фиксированными пропорциями (5). Решение этой проблемы идентификации представляется целесообразным рассмотреть с позиций теории распознавания образов.
коэффициента регрессии в зависимости (3). Такое решение позволяет оценить с определенной долей вероятности предпочтительность предельных вариантов CES-функций: функции Кобба-Дугласа (4) или функции с фиксированными пропорциями (5). Решение этой проблемы идентификации представляется целесообразным рассмотреть с позиций теории распознавания образов. и
и  , а для характеристики объектов используется признак
, а для характеристики объектов используется признак  и
и  значений признака объектов классов
значений признака объектов классов  распознаваемого объекта.
распознаваемого объекта. и следующее правило принятия решений: если наблюдаемое значение признака у ра
и следующее правило принятия решений: если наблюдаемое значение признака у ра


