Черкаси 2009 4 страницаТому для опису таких функцій застосовують інші типи опису. Для опису складних функцій можуть застосовуватися інші поліноми (поліном Ньютона, ортогональні поліноми Чебишева, Лежандра, Ерміта та ін.) з рівновіддаленими чи адаптивнопідібраними вузловими точками. Але існує інший метод наближення – інтерполювання сплайнами.
5.2. Сплайн-інтерполяція
При сплайн-інтерполяції зберігається умова проходження наближуючої функції через вузлові точки. Сплайн (spline) переводиться з англійської, як гнучка лінійка. Сплайн-функції різняться ступенем поліному, що зображає функцію. Сутністю сплайн-інтерполяції є моделювання фрагментів заданої функції рядом поліномів низького ступеню. Прикладом такого інтерполювання є кусково-лінійне інтерполювання (рис. 5.1), де кожна з функцій будується по двом сусіднім вузловим точкам. Такий же принцип побудови зберігається і для формування поліномів вищих порядків, тільки кількість точок, на основі яких будується кожен з поліномів може бути більшою. Так, наприклад, для кусково-квадратичного поліному на проміжку [ x0, xN ] береться кожен інтервал [ x2k, x2k+2 ] для побудови на ньому квадратичного поліному. Але при побудові такого сплайну кривизна в парних вузлах різко змінюється, що відбивається на якості апроксимації.
Найбільш оптимальною на даний момент є кусково-кубічна сплайн-інтерполяція [4, 11-13]. Вона широко застосовується у системах комп‘ютерної графіки та системах проектування з використанням комп‘ютера: CAD-системах (системи комп‘ютеризованої допомоги в дизайні та кресленні) та GІS-системах (географічні інформаційні системи). За допомогою цього виду інтерполяції можливо побудувати гладку криву, що проходить через задані точки. Означення. Припустимо, задані (N+1) точки, де їх абсциси хі задовольняють умові а = x0 < x1 < …< xN = b. Функція S(х) називається кубічним сплайном, якщо існують N кубічних поліномів Sk(х) з коефіцієнтами sk, 0, sk, 1, sk, 2 та sk, 3, що задовольняють наступним умовам: 1) S(x) = Sk(x) = sk, 0 + sk, 1(x-xk) + sk, 2(x-xk)2 + sk, 3(x-xk)3, де х Î [xk, xk+1], k = 0, 1, …, N-1; 2) кусочно-кубічний поліном (сплайн) заданий сукупністю точок S(xk) = yk, де k = 0, 1, …, N; 3) сплайн-функція складається з поліномів (гладких функцій), які сполучуються у вузлових точках Sk(xk+1) = Sk+1(xk+1), де k = 0, 1, …, N-2; 4) сплайн-функція буде неперервною, якщо існує і безперервна її перша похідна S’k(xk+1) = S’k+1(xk+1), де k = 0, 1, …, N-2; 5) радіус кривизни сплайн-функції визначений в кожній точці (гладкість функції), якщо існує і безперервна її друга похідна S’’k(xk+1) = S’’k+1(xk+1), де k = 0, 1, …, N-2. Загальний вираз для кубічної сплайн-функції Sk(x) має вигляд:
Кубічний поліноми для утворення сплайн-функції будується по трьом сусіднім точкам за загальною формулою:
де При формуванні сплайн-функції будуються N-1 рівнянь з N+1 змінними. Для їх розв‘язання систему треба доповнити двома додатковими рівняннями. В якості таких рівнянь вибирають обмеження в крайніх точках сплайну, що наведені в таблиці 5.1. Таблиця 5.1 Обмеження в крайніх точках кубічного сплайну [4].
Розглянемо побудову зімкненого кубічного сплайну. Якщо відома перша похідна у початковій точці, можна обчислити m 0 і перше рівняння прийме вигляд:
Аналогічно обчислюємо останнє рівняння:
Отримуємо тридіагональну лінійну систему рівнянь:
Коефіцієнти сплайну обчислюємо за формулами:
Для зручності обчислень кожен кубічний сплайн доцільно записувати у формі вкладених перемножень:
де У випадку константного задавання обмежень частину експериментальних точок на початку і вкінці проміжку «обрізають» для усунення великих похибок, які виникають в цих діапазонах. Тому при плануванні експерименту такі обчислювальні особливості потрібно враховувати. Приклад 1. Обчислимо зімкнений кубічний сплайн, що проходить через точки (0, 0), (1, 0.5), (2, 2) та (3, 1.5). Перша похідна задовольняє граничним умовам
h0 = h1 = h2 = 1; d0 = (y1 – y0)/h0 = (0.5 - 0)/1 = 0.5; d1 = (y2 – y1)/h1 = (2.0 – 0.5)/1 = 1.5; d2 = (y3 – y2)/h2 = (1.5 - 2)/1 = - 0.5; u1 = 6(d1 – d0) = 6(1.5 – 0.5) = 6; u2 = 6(d2 – d1) = 6(-0.5 – 1.5) = -12. Складемо основні рівняння (перше і останнє рівняння складають за формулами з табл. 5.1., інші рівняння – за формулою (5.14)):
Підставимо конкретні значення:
При спрощенні системи отримаємо:
Обчислимо значення m1 = 2.52 та m2 = -3.72 Скористаємося додатковими рівняннями з таблиці 5.1:
Підставимо розраховані значення у формули (5.18), за якими обчислимо коефіцієнти сплайн-функцій. Отримаємо наступні вирази сплайн-функцій:
Графічний розв‘язок системи поданий на рис. 5.4.
Рис. 5.4. Зімкнений кубічний сплайн.
Приклад 2. При формуванні у середовищі MatLAB [14] зімкненого кубічного сплайну, який проходить через точки (0, 0.0), (1, 0.5), (2, 2.0), (3, 1.5), з першою похідною у граничних точках S’(0) = 0.2; S’(3) = -1, функція задається так:
> > X = [0 1 2 3]; Y = [0 0.5 2.0 1.5]; dx0 = 0.2; dxn = -1; > > S = zspline (X, Y, dx0, dxn) S = 0.4800 -0.1800 0.2000 0 -1.0400 1.2600 1.2800 0.5000 0.6800 -1.8600 0.6800 2.0000 Графік сплайну будують, використовуючи команду polyval, яку потрібно задавати для кожного відрізка сплайну окремо:
> > x1 = 0:.01: 1; y1 = polyval (S(1,:), x1-X(1)); > > x2 = 1:.01: 2; y2 = polyval (S(2,:), x2-X(2)); > > x3 = 2:.01: 3; y3 = polyval (S(3,:), x3-X(3)); > > plot (x1, y1, x2, y2, x3, y3, X, Y, ’.’)
Контрольні питання 1. Що називається інтерполяцією та екстраполяцією? 2. Від яких чинників залежить точність інтерполяції? 3. Який принцип апроксимації функцій поліномом Лагранжа? 4. Що називається кубічної сплайн-функції? Які умови забезпечують неперервність та гладкість сплайн-функції? 5. Які бувають види кубічних сплайнів в залежності від обмежень в крайніх точках і які з них дозволяють отримати найвищу точність? 6. Чому точність інтерполяції кубічною сплайн-функцією вища ніж поліномом Лагранжа? Розділ 6. Апроксимація експериментальних даних. Метод найменших квадратів. Інтерполяція функцій за допомогою ортогональних поліномів 6.1. Апроксимація експериментальних даних. Метод найменших квадратів При проведенні експериментів дослідник отримує дані, які є наближеними через неточність вимірювальних приладів, неточності відтворення умов спостережень, випадкові помилки та інші чинники. Для відновлення функції результатів спостережень або для заміни складної функції простішою для прискорення розрахунків часто використовують метод найменших квадратів. Розглянемо задачу відновлення функції
де
де У випадку, коли k = n (формула 6.2) функція j (х) збігається з інтерполяційним поліномом Лагранжа, побудованим по тих же вузлових точках. Для мінімізації цільової функції 6.1, функціоналу, необхідно, щоб перші похідні функціоналу І за його аргументами
Обчислимо похідні функціоналу по невідомих:
Проведемо заміну:
Обчислимо наступні похідні:
Отримаємо рівняння:
У загальному випадку похідні функціоналу по невідомих:
Отримаємо систему рівнянь:
Якщо система має єдиний розв‘язок, то він визначає коефіцієнти полінома найкращого середньоквадратичного наближення. Отриманий поліном Приклад. Запишемо систему рівнянь, складену за методом найменших квадратів для функціонала:
Якість апроксимації експериментальних даних поліномом j (х) оцінюється залишковою дисперсією:
де p – число ступенів свободи, яке обчислюється як різниця між числом дослідних значень n і кількістю коефіцієнтів апроксимуючого поліному m (p = n – m). Для функцій з різною кількістю коефіцієнтів апроксимуючого поліному значення дисперсії будуть різними, з них вибирають той, який має найменше значення
6.2. Інтерполяція функцій ортогональними поліномами
Альтернативою методу найменших квадратів є метод, що оснований на використанні скалярних добутків базисних функцій [5, 11]. Якщо кожне рівняння системи:
помножити на відповідну базисну функцію jj (х), j = 0, 1, …, m, отримаємо систему рівнянь у нормальний формі:
Система має (m+1) рівнянь відносно невідомих коефіцієнтів cj , j=0, 1, …, m за значеннями функції f, що визначена на множині точок xi , i=0, 1, …, n для будь-якого n ≥ т. Збільшення числа вузлових точок впливає лише на точність визначення скалярних добутків і не збільшує розмірності системи рівнянь. Якщо в якості базисних функцій вибрати ортогональні поліноми (Лежандра, Чебишева, Ерміта та ін.), для яких
У цьому випадку похибка ортогональна до всіх jj (х), j = 0, 1, …, m, тобто:
Спільною характеристикою для ортогональних поліномів є форма системи рівнянь:
У загальному випадку систему можемо записати:
У даній системі
звідки:
Тобто, будь-який поліном n -го ступеню може бути представлений сукупністю базисних ортогональних поліномів виду:
Такий алгоритм дозволяє проводити наближення функції ортогональними поліномами за допомогою множення на відповідну базисну функцію (6.13), а потім представляти наближення звичайною поліноміальною формою (6.20). Загальні формули ортогональних поліномів Лежандра, Чебишева і Ерміта наведені в таблиці 6.1. *** Апарат кусочно-лінійної інтерполяції (див. розділ 5) дозволяє ввести об‘єкти, на яких базується один із найбільш відомих сучасних сіткових чисельних методів — метод кінцевих елементів (п. 10.2.2). Досліджувана область розбивається сіткою, в загальному випадку нерівномірною. Вузлам сітки {tn} ставиться у відповідність набір базисних функцій jn(t), кожна з яких відповідає певному вузлу tn, до того ж jn(tk)=dkn , jn(tk-1) = jn(tk+1) = 0, jn(tn)=1, а в інших точках вона обчислюється за допомогою кусково-лінійної інтерполяції.
Таблиця 6.1. Властивості ортогональних поліномів [5]
Узагальнений інтерполяційний поліном F(t) в даному випадку можемо записати у вигляді:
В обчислювальній математиці часто використовується кусково-поліноміальна інтерполяція. Так, эрмітовим кубічним інтерполянтом називається кусково-кубічний інтерполянт з неперервною першою похідною, кубічним сплайном називається кусково-кубічний інтерполянт з двома першими неперервними похідними.
6.3. Базисні сплайни (В-сплайни)
Сплайни з локальним носієм називають базисними сплайнами (B-сплайнами). Останнім часом в обчислювальній практиці широке розповсюдження набули B-сплайни (від англійського слова bell — дзвін (колокол)), зосереджені на скінченному відрізку [7, 11]. Вони використовуються як для інтерполяції функцій, так і в якості базисних функцій при побудові методів типу скінченних елементів. B-сплайном (базисним сплайном) ступеню n-1 дефекту 1 відносно вузлів
де Припустимо область розв‘язку задачі розбита рівномірною сіткою При N = 2 В-сплайн (1-го порядку) будується найпростіше:
або
Рис. 6.1. В-сплайн першого порядку.
В-сплайн 2-го порядку запишемо у вигляді:
При а) б) в) При інтерполяції функції можемо додати граничні умови. Для інтерполяції за допомогою сплайну необхідно виконання умови:
де b — коефіцієнти інтерполяції, S — B-сплайн, індекс вказує на точку, для якої побудований сплайн і в якій він досягає максимуму. Система таких співвідношень, доповнюється граничними умовами. Отримана система для визначення коефіцієнтів розкладу буде мати тридіагональну матрицю з діагональною перевагою при виконанні обмеження на довжину сусідніх кроків: вони повинні різнитися не більше ніж в Кубічний В-сплайн (N = 4) має вигляд:
Після деяких спрощень можемо записати попередню формулу у вигляді:
Рис. 6.2. Графік кубічного В-сплайну.
Базисні сплайни (В-сплайни) заданого ступеню є лінійно незалежними функціями і утворюють базис в функціональних просторах, цю властивість можемо використати для представлення за їх допомогою інших функцій цих же просторів. Будь-яка, наприклад, кусково-постійна функція на відрізку, що вміщує інтервали рівної довжини, може бути єдиним чином представлена лінійною комбінацією В-сплайнів нульового ступеню, будь-яка кусково-лінійна функція — В-сплайнів першого ступеню і т.і. Базисні сплайни відіграють значну роль при побудові чисельних методів розв‘язання задач математичної фізики, наприклад, метода скінченних елементів в теорії наближень функцій, при розв‘язку задач комп‘ютерної графіки та інших [15, 17]. Контрольні питання 1. Для яких задач використовують метод найменших квадратів? 2. В чому полягає суть методу найменших квадратів? 3. Як будується поліном найкращого середньоквадратичного наближення? 4. Яке рівняння називається рівнянням регресії? 5. Як оцінюється якість апроксимації експериментальних даних? 6. Назвіть види ортогональних поліномів? 7. Що називається базисним сплайном (В-сплайном)? 8. Назвіть види базисних сплайнів? Для яких задач вони застосовуються? Частина 2.Чисельне диференціювання та інтегрування. Роз‘вязання диференційних рівнянь. Розділ 7. Чисельне диференціювання та чисельне інтегрування 7.1. Чисельне диференціювання
У випадках, коли похідну функції, яка задана аналітично, тяжко обчислити по причині її складності чи тому, що похідна набуває незручну для застосування форму, використовують чисельне (наближене) диференціювання. Цей метод незамінний, коли функція задана таблично. Найбільш розповсюджені способи чисельного диференціювання – використання скінченних різниць та інтерполяційних поліномів. Розглянемо їх послідовно.
7.1.1. Використання скінченних різниць
Звернемося до класичного визначення похідної. За визначенням похідна функції f(х) є нова функція, що дорівнює при кожному значенні х границі відношення прирощення функції (
|

 , (5.13)
, (5.13) (5.14)
(5.14) ,
,  ,
,  , де в свою чергу
, де в свою чергу  .
. ,
, 


 в крайніх обмежуючих точках
в крайніх обмежуючих точках


 ,
, 
 (5.15)
(5.15) (5.16)
(5.16) (5.17)
(5.17) (5.18)
(5.18) , (5.19)
, (5.19) . При побудові сплайнів зі складними обмеженнями в крайніх точках, що враховують першу похідну, як, наприклад, в зімкненому кубічному сплайні, отримуємо більш точний результат, ніж при константному здаванні значень другої похідної (2 та 4 сплайни в таблиці 5.1). Найкращий результат отримуємо при екстраполяційному задаванні других похідних. Це пояснюється адаптивністю даних обмежень відносно вхідних даних, що дозволяє точніше враховувати особливості функції не тільки в середині проміжку інтерполяції, а і біля кінців проміжку, де похибка апроксимації досягає найбільших значень.
. При побудові сплайнів зі складними обмеженнями в крайніх точках, що враховують першу похідну, як, наприклад, в зімкненому кубічному сплайні, отримуємо більш точний результат, ніж при константному здаванні значень другої похідної (2 та 4 сплайни в таблиці 5.1). Найкращий результат отримуємо при екстраполяційному задаванні других похідних. Це пояснюється адаптивністю даних обмежень відносно вхідних даних, що дозволяє точніше враховувати особливості функції не тільки в середині проміжку інтерполяції, а і біля кінців проміжку, де похибка апроксимації досягає найбільших значень. = 0.2 та
= 0.2 та  = -1. Обчислимо проміжні величини:
= -1. Обчислимо проміжні величини:

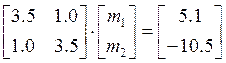



 результатів спостережень методом найменших квадратів [6]. Це задача мінімізації функціоналу. При її розв‘язанні необхідно забезпечити мінімум міри відхилень експериментальних значень від обраної функції в (n+1) вузлових точках (хі , уі). Цільову функцію для цієї умови запишемо у вигляді:
результатів спостережень методом найменших квадратів [6]. Це задача мінімізації функціоналу. При її розв‘язанні необхідно забезпечити мінімум міри відхилень експериментальних значень від обраної функції в (n+1) вузлових точках (хі , уі). Цільову функцію для цієї умови запишемо у вигляді: (6.1)
(6.1) – базисні функції. Найчастіше базисні функції
– базисні функції. Найчастіше базисні функції  (6.2)
(6.2) – коефіцієнти узагальненого полінома. Тобто, побудова полінома найкращого середньоквадратичного наближення для заданої функції
– коефіцієнти узагальненого полінома. Тобто, побудова полінома найкращого середньоквадратичного наближення для заданої функції  у рівнянні (6.2). Для розв‘язання цієї задачі використаємо метод найменших квадратів.
у рівнянні (6.2). Для розв‘язання цієї задачі використаємо метод найменших квадратів. дорівнювали нулю (необхідна умова екстремуму функції [7]):
дорівнювали нулю (необхідна умова екстремуму функції [7]): (6.3)
(6.3) (6.4)
(6.4)
 (6.5)
(6.5) (6.6)
(6.6) (6.7)
(6.7) (6.8)
(6.8) (6.9)
(6.9) називається рівнянням регресії.
називається рівнянням регресії. .
. (6.10)
(6.10) (6.11)
(6.11) .
. (6.12)
(6.12)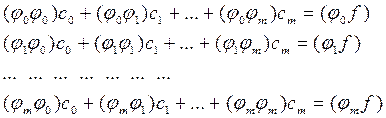 (6.13)
(6.13) , i ≠ j,
, i ≠ j,  , обчислення коефіцієнтів cj значно спрощується:
, обчислення коефіцієнтів cj значно спрощується: (6.14)
(6.14) (6.15)
(6.15) (6.16)
(6.16) (6.17)
(6.17) – нижня трикутна матриця порядку (m+1). Розв‘язок задачі знайдемо з рівняння:
– нижня трикутна матриця порядку (m+1). Розв‘язок задачі знайдемо з рівняння: (6.18)
(6.18) (6.19)
(6.19) (6.20)
(6.20)


















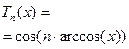

 (6.21)
(6.21) називається функція:
називається функція: (6.22)
(6.22) .
. . Розглянемо кілька частинних випадків В-сплайнів.
. Розглянемо кілька частинних випадків В-сплайнів. (6.23)
(6.23) (6.24)
(6.24)
 (6/25)
(6/25)  ,
, 
 . Побудований сплайн має наступні властивості:
. Побудований сплайн має наступні властивості: ,
, , (6.26)
, (6.26) .
. , (6.27)
, (6.27) рази.
рази. (6.29)
(6.29)

 ) до відповідного прирощення аргументу Δ x, тобто:
) до відповідного прирощення аргументу Δ x, тобто:


