Черкаси 2009 5 страница
Геометричний сенс похідної. Похідна функції в точці х є тангенсом кута нахилу дотичної до графіку функції в цій точці, якщо кут відраховується від позитивного напрямку осі ОХ проти годинникової стрілки (рис. 7.1):
Якщо перейти від нескінченно малих різниць (
Рис. 7.1. Геометричний сенс похідної функції.
За формулою 7.2 можемо обчислити значення похідної функції f(х) в точці х при заданому значенні прирощення Δ x. Заміна нескінченно малих Δ x на кінцеві викликає появу похибок, що є похибками методу. Для оцінки цих похибок розкладемо функцію f(х) в точці (x + Δ x) в ряд Тейлора:
При підстановці формули (7.3) у формулу (7.2) отримаємо наступний вираз:
З отриманої рівності бачимо, що елементи ряду, починаючи з другого, визначають відмінність числового значення похідної від її точного значення. Основним елементом похибки є значення
При обчисленні похідної за симетричною формулою:
можемо обчислити похибку за тим же методом. Похибка цієї формули дорівнює При аналізі похибок загальну похибку чисельного диференціювання представимо рівнянням:
де Емет – похибка методу, Еобч – похибка обчислень, Для симетричної формули похибку чисельного диференціювання запишемо у вигляді:
Якщо
Знайдемо значення
Використовуючи симетричну формулу четвертого порядку (О(
У даному прикладі похибку методу запишемо у вигляді:
Загальна похибка чисельного диференціювання:
Визначення кроку диференціювання проводимо за формулою:
7.1.2. Чисельне диференціювання на основі інтерполяційної формули Лагранжа
Розглянемо поліном Лагранжа з рівновіддаленими вузлами (розділ 5, п. 5.1):
де Проведемо заміну:
При диференціюванні поліному Лагранжа, беручи до уваги, що
З цієї формули отримуємо деякі загальні формули для правих і лівих різниць порядку (О(h)2):
Аналогічно отримують різницеві формули для визначення других похідних:
Використовуючи різницеві формули можемо розрахувати значення похідної функції з рівновіддаленими вузлами у вузловій точці по значеннях функції у сусідніх вузлових точках.
7.1.3. Застосування похідних Якщо величина у залежить від х, то швидкість змінення значень у в залежності від х визначається як Для визначення швидкості змінення показників в багатьох задачах фізики, техніки, економіки, соціології застосовується диференціювання. Якщо про диференціювати необхідно функцію, похідну якої складно обчислити, застосовують чисельне диференціювання Якщо задана точність e, з якою необхідно отримати значення похідної f¢ (х), то обчислюємо величину відстані між сусідніми точками Δ x за формулами 7.9, 7.13. Диференціювання у Matlab. Для отримання значень похідних функції, що задана таблично, використовують внутрішні функції Matlab [11]: · diff (X) – повертає кінцеві різниці, обчислені по суміжним елементам вектора Х. Довжина вектора, що повертається функцією diff (X), на одиницю менше ніж довжина вектора Х. Якщо Х = матриця, то функція повертає матрицю, що вміщує кінцеві елементи, які обчислені по кожному стовпцю; · diff (X, n) – повертає кінцеві різниці n –го порядку; · diff (X, n, dim) – повертає кінцеві різниці n –го порядку по стовпцям (dim = 1) чи рядкам матриці.
7.2. Чисельне інтегрування
В наукових та інженерних задачах часто потрібно обчислювати визначені інтеграли. Але не всі вони мають аналітичний розв’язок. Для знаходження таких інтегралів застосовуються методи чисельного інтегрування.
Рис. 7.2. Фізичний сенс інтегралу.
Класично визначений інтеграл обчислюється за формулою Ньютона-Лейбница:
Але ця формула малопридатна для практичного застосування, оскільки клас функцій, для яких первісні
Задача чисельного інтегрування полягає у знаходженні визначеного інтегралу від функції f(x) на інтервалі [ a, b ], обчислюючи функцію f(x) на скінченій множині підінтервалів (рис. 7.3).
Рис. 7.3. Дискретизація області визначення задачі чисельного інтегрування.
Виберемо проміжні точки так, щоб a = x0 < x1 < … < xM = b. Формулою чисельного інтегрування або формулою квадратури називають:
яка відповідає визначеному інтегралу
У формулі Ступінь точності формули квадратури дорівнює позитивному цілому числу n, такому що E[Pi] = 0 для всіх поліномів Pi(х) ступеня i £ n, але водночас E[Pn+1] ¹ 0 у випадку поліному Pn+1(x) ступеня (n+1). Формула для помилки інтегрування має вигляд:
де К – константа, n – ступінь точності.
7.2.1. Квадратурні формули інтерполяційного типу Щоб отримати інтерполяційну формулу для складних функцій нерідко використовують інтерполяційні поліноми, що наближено описують ці функції. За визначенням існує єдиний поліном (зазначеного типу) PМ(х) ступеня £ М, який проходить через (М+1) рівновіддалених точок. При використанні поліному Лагранжа з рівновіддаленими вузлами для наближення функції f(x) на інтервалі [ a, b ], інтеграл від f(x) наближено обчислюється за допомогою інтегралу від PL(х), в результаті отримуємо формулу квадратури Ньютона-Котеса (Newton-Cotes). Коли початкова і кінцева точки х0 = а та хМ = b, формулу називають замкнутою. Формули для наближення поліномами М = 1, 2, 3 та 4 ступеню відповідно наведені у таблиці 7.1, схеми визначення інтегралу за формулами квадратури подані на рисунку 7.4. Таблиця 7.1 Формули квадратури Ньютона-Котеса [4]
Рис. 7.4. Схеми визначення інтегралу за формулами квадратури.
7.2.2. Замкнуті формули квадратури Ньютона-Котеса
При обчисленні інтегралу можемо отримати проміжних точок більше, ніж використовується у формулі квадратури. Тому для обчислення інтегралу на всьому заданому проміжку скористаємося складною формулою квадратури. Так складна формула трапецій має вигляд:
Складна формула Сімпсона:
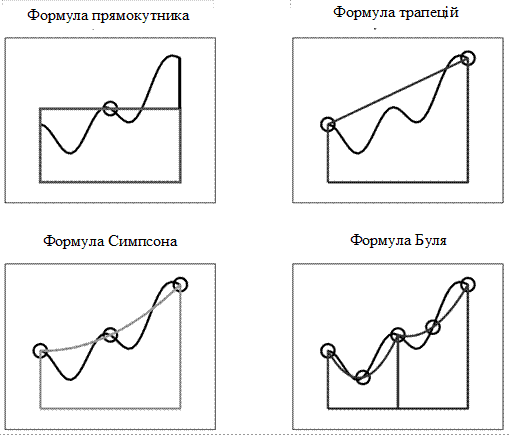
Для того, щоб формула квадратури була замкнутою, потрібно, щоб кількість вузлових точок на проміжку [ a, b ] була кратною числу точок, на яких будується вибрана формула квадратури з врахуванням початкової та кінцевої точок кожної локальної формули квадратури (рис. 7.5).
Рис. 7.5. Розрахунок визначеного інтегралу за замкнутою формулою Симпсона.
З рисунку 7.5 бачимо, що для розрахунку визначеного інтегралу на проміжку [ х0, х8 ] інтервал розбили на 4 підінтервали, формула Сімпсона використовувалася 4 рази. Якщо позначити кількість точок, що використовується в простій формулі Сімпсона n = 3 і число застосувань формули m = 4 (значення функції в точках х2, х4, х6 використовуються двічі), то розрахунок кількості вузлів матиме вигляд:
Контрольні питання 1. В чому полягає суть чисельного диференціювання? 2. Що називається різничними аналогом похідної? Які існують види різничних аналогів? 3. В чому полягає задача чисельного інтегрування? 4. Що називається формулою квадратури? 5. Які існують формули квадратури Ньютона-Котеса? Як здійснюється оцінка точності формул квадратури Ньютона-Котеса? 6. Що називається замкнутою квадратурною формулою? Як формується замкнута формула квадратури? Розділ 8. Чисельні методи розв’язання задачі Коші для звичайних диференційних рівнянь
8.1. Основні поняття
При побудові динамічних математичних моделей технічних і природничих об’єктів часто приходять до розв’язку звичайного диференційного рівняння чи системи диференційних рівнянь, що задовольняють певній початковій умові (задача Коші). В небагатьох випадках можливо проінтегрувати таке рівняння у скінченому вигляді, але навіть якщо інтегрування можливе, то шукана функція часто входить до розв’язку у неявному вигляді, що не зручно для подальшого використання у математичних розрахунках. Для розв’язання таких задач використовують чисельне (наближене) інтегрування диференційних рівнянь.
Задача Коші полягає у знаходженні розв’язку у(х) диференційного рівняння
який задовольняє початковій умові
При геометричній інтерпретації розв’язку задачі – треба знайти інтегральну криву у(х) рівняння (8.1), яка проходить через точку (х0, у0). При розгляді рис. 8.1 інтегральна крива, що відповідає початковій умові Задача Коші має єдиний розв’язок при виконанні наступної теореми. Теорема Пікара: Якщо функція f(х, у) двох змінних х і у неперервна у замкненому прямокутнику з центром у точці (х0, у0)
і задовольняє в ньому умові Ліпшиця по змінній у, тобто існує число К > 0, яке не залежить від х і у, таке, що
для будь-яких точок
Рис. 8.1. Множина інтегральних кривих, що є розв‘язком диференційного рівняння
При розгляді, наприклад, фізичної системи у – вектор фазових змінних (розмірністю n), які характеризують запас енергії у системі, х часто є часом перебігу реального процесу. При чисельному розв‘язанні рівняння отримують значення у(х) на потрібному інтервалі часу, наприклад 0 … tк, при заданих початкових умовах (формула 8.2). При розв’язанні задачі на проміжку інтегрування виділяють певне число точок tm, у яких розраховують значення у(х). Інтервал між сусідніми точками називають кроком інтегрування і позначають:
Знайти послідовність вузлових точок при h = соnst дозволяє формула:
До методу чисельного розв‘язку (інтегрування) диференційних рівнянь пред’являються наступні основні вимоги: · універсальність, тобто можливість застосування до будь-якого об’єкту із заданого класу, · алгоритмічна надійність, · достатня точність результатів, · помірні затрати машинного часу і пам’яті. Основними характеристиками методів інтегрування, від яких залежить їх ефективність, є точність і стійкість методів, а також пов’язана з ними стратегія вибору величини кроку інтегрування. Точність інтегрування залежить від таких основних складових: ¨ похибки апроксимації (похибки методу інтегрування); ¨ похибки обчислень, що пов’язана з похибками округлення чисел у персональному комп‘ютері і заміною неарифметичних операцій та функцій арифметичними; ¨ похибки накопичення, яка дорівнює повній похибці на попередньому кроці. Стійкість методів чисельного інтегрування пов’язана з характером змінення накопиченої похибки. Якщо похибка у ході інтегрування значно не зростає зі збільшенням числа кроків, а змінюється у деяких допустимих межах, то використовуваний метод інтегрування буде чисельно стійким. Якщо навіть при невеликих помилках апроксимації чи обчислень накопичена похибка зростає від кроку до кроку, то використовуваний метод інтегрування нестійких при даних величинах кроків, а результати таких обчислень не несуть потрібної інформації. Оцінку кроку інтегрування можливо отримати, дослідивши власні значення матриці коефіцієнтів системи рівнянь. У загальному випадку власні значення – комплексні величини, тобто Крок інтегрування знаходиться із співвідношення hm < 2tmin, де tmin – мінімальна постійна часу системи. Постійна часу системи знаходиться з виразу:
Для розв’язання задачі Коші використовують методи Гюна, Тейлора, Ейлера (явний, неявний та модифікації), а також методи Рунге-Кутта. 8.2. Явний метод Ейлера У даному методі значення знаходяться по значеннях функції у попередній точці починаючи від х 0. Наступне значення функції по значеннях у попередній к -тій точці можна знайти за формулою:
Якщо класичними методами розв’язати задачу не вдається, користуються формулою Ейлера, в якій інтеграл наближено обчислюють за формулою лівих прямокутників:
Геометричну інтерпретацію методу Ейлера можемо представити таким чином: якщо побудувати дотичну до графіку функції у(х) в точці х0, яка описується рівнянням При побудові на наступних інтервалах дотичної до функції у(х) отримаємо ламану криву, яку називають ламаною Ейлера [5].
Рис. 8.2. Геометрична інтерпретація методу Ейлера.
Алгоритм явного методу Ейлера: 1. Задавання початкових значень і початкових даних х0 , хкін , у(х0) = у0 , eдоп (останній параметр нерідко обчислюється). 2. Обчислення власних значень матриці коефіцієнтів системи. 3. Визначення кроку hm < 2tmin. 4. Виконання ітерації за формулою Ейлера (8.6). 5. Перехід до наступної вузлової точки хк+1 = хк + h і вивід результатів. 6. Якщо хк+1< xкін, то перейти до пункту 4, інакше завершити ітерації.
Приклад 8.1. 1. Розв’яжемо систему звичайних диференційних рівнянь:
2. Початкові умови х1, 0 = х2, 0 = 0. 3. Обчислимо розв’язки характеристичного рівняння
4. Виберемо крок інтегрування. Постійні часу системи, обчислені за формулою (8.4), t1 = 1, t2 = 6 Þ tmin = 1. Звідси h < 2tmin, h < 2. Керуючись обмеженням h < 2 та необхідною точністю обчислень приймаємо h = 0, 3. 5. Обчислюємо послідовно значення функції за формулою Ейлера: 1) х1, 0 = 0, х2, 0 = 0. 2) 3)
4) наступні ітерації аналогічно … Явний метод Ейлера ефективний тільки для розрахунку систем звичайних диференційних рівнянь з малим розсіюванням постійних часу, тому що він є обмежено стійким методом інтегрування [3, 4]. Крім того, зустрічаються задачі, де
8.3. Неявний метод Ейлера
Формула інтегрування неявного методу Ейлера відрізняється від формули явного методу обчисленням значень у наступній точці по значеннях
Особливістю цієї формули інтегрування є необхідність розв’язувати систему рівнянь на кожному кроці інтегрування відносно змінної
Обчислення за формулою 8.9 починаємо з 4-ї ітерації, оскільки для розрахунку потрібні значення
|

 (7.1)
(7.1) .
. ) до кінцевих різниць, отримаємо формулу чисельного диференціювання:
) до кінцевих різниць, отримаємо формулу чисельного диференціювання: (7.2)
(7.2)
 (7.3)
(7.3) (7.4)
(7.4) . Вважають, що така похибка має перший порядок точності по Δ x, тобто O(Δ x).
. Вважають, що така похибка має перший порядок точності по Δ x, тобто O(Δ x).  (7.5)
(7.5) , вона має другий порядок точності по Δ x, тобто O(Δ x)2.
, вона має другий порядок точності по Δ x, тобто O(Δ x)2. (7.6)
(7.6)
 ,
,  і
і  .
. (7.7)
(7.7) ,
,  і
і  , то
, то (7.8)
(7.8) (крок диференціювання), що мінімізує праву частину рівняння (7.7) з врахуванням симетричності формули диференціювання:
(крок диференціювання), що мінімізує праву частину рівняння (7.7) з врахуванням симетричності формули диференціювання: (7.9)
(7.9) )4) для обчислення першої похідної отримаємо:
)4) для обчислення першої похідної отримаємо: (7.10)
(7.10) (7.11)
(7.11) (7.12)
(7.12) (7.13)
(7.13) ,
,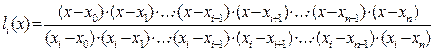 .
. . Тоді поліном Лагранжа можемо записати у такому вигляді:
. Тоді поліном Лагранжа можемо записати у такому вигляді: (7.14)
(7.14) , отримаємо:
, отримаємо: (7.15)
(7.15)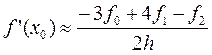 (права різниця) (7.16)
(права різниця) (7.16) (ліва різниця) (7.17)
(ліва різниця) (7.17) (права різниця) (7.18)
(права різниця) (7.18) (ліва різниця) (7.19)
(ліва різниця) (7.19) . Наприклад швидкість змінення тиску p в залежності від висоти h запишемо як
. Наприклад швидкість змінення тиску p в залежності від висоти h запишемо як  . Якщо мова йде про швидкість змінення величини в залежності від часу то говорять: «швидкість змінення величини», а слова «в залежності від часу» пропускають. Наприклад швидкість змінення току запишемо
. Якщо мова йде про швидкість змінення величини в залежності від часу то говорять: «швидкість змінення величини», а слова «в залежності від часу» пропускають. Наприклад швидкість змінення току запишемо  .
. , суть якого полягає в розбитті області визначення змінної х, де
, суть якого полягає в розбитті області визначення змінної х, де  , на відрізки a = x0 < x1 < … < xn = b і обчислення на кожному з них значення похідної за різницевою формулою, наприклад, формулою (7.2) чи більш точними формулами, після чого знаходять суму всіх отриманих значень. Таким чином, отримуємо наближене значення похідної, точність якого залежить від виду функції f(х), відстані між сусідніми вузловими точками, точності формули чисельного диференціювання. Точність чисельного диференціювання оцінюємо за відповідною формулою похибок (формули 7.8, 7.11).
, на відрізки a = x0 < x1 < … < xn = b і обчислення на кожному з них значення похідної за різницевою формулою, наприклад, формулою (7.2) чи більш точними формулами, після чого знаходять суму всіх отриманих значень. Таким чином, отримуємо наближене значення похідної, точність якого залежить від виду функції f(х), відстані між сусідніми вузловими точками, точності формули чисельного диференціювання. Точність чисельного диференціювання оцінюємо за відповідною формулою похибок (формули 7.8, 7.11). В основу чисельних методів інтегрування закладений фізичний сенс визначеного інтеграла. Визначений інтеграл дорівнює площі фігури, що обмежена неперервною підінтегральною функцією f(x) на проміжку [ a, b ] (рис. 7.2).
В основу чисельних методів інтегрування закладений фізичний сенс визначеного інтеграла. Визначений інтеграл дорівнює площі фігури, що обмежена неперервною підінтегральною функцією f(x) на проміжку [ a, b ] (рис. 7.2).
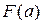 та
та 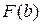 можна виразити через елементарні функції дуже вузький. Крім того, часто на практиці підінтегральна функція задається таблицею і саме поняття первісної втрачає сенс. Тому в наш час для обчислення інтегралів велике розповсюдження отримали чисельні методи.
можна виразити через елементарні функції дуже вузький. Крім того, часто на практиці підінтегральна функція задається таблицею і саме поняття первісної втрачає сенс. Тому в наш час для обчислення інтегралів велике розповсюдження отримали чисельні методи.
 (7.20)
(7.20) (7.21)
(7.21) – похибка інтегрування. Вона має сенс лише тоді, коли функція f(x) задана аналітично. Функції
– похибка інтегрування. Вона має сенс лише тоді, коли функція f(x) задана аналітично. Функції  називають ваговими коефіцієнтами. Вузлові точки для чисельного інтегрування можуть вибиратися рівновіддаленими, як у формулах Сімпсона чи Буля, або розташованими за певними правилами, як для формули Гаусса-Лежандра [4, 6].
називають ваговими коефіцієнтами. Вузлові точки для чисельного інтегрування можуть вибиратися рівновіддаленими, як у формулах Сімпсона чи Буля, або розташованими за певними правилами, як для формули Гаусса-Лежандра [4, 6]. (7.22)
(7.22)






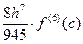
 (7.23)
(7.23) (7.24)
(7.24) (7.25)
(7.25) (7.26)
(7.26)
 . Аналогічно розраховується кількість точок за іншими формулами квадратури.
. Аналогічно розраховується кількість точок за іншими формулами квадратури. , (8.1)
, (8.1) (8.2)
(8.2)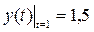 має коефіцієнт С = 0.
має коефіцієнт С = 0.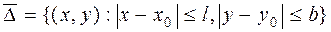
 (8.3)
(8.3) та
та  , то існує єдина диференційована функція
, то існує єдина диференційована функція  , яка є розв’язком диференційного рівняння (8.1), що задовольняє початковій умові (8.2).
, яка є розв’язком диференційного рівняння (8.1), що задовольняє початковій умові (8.2).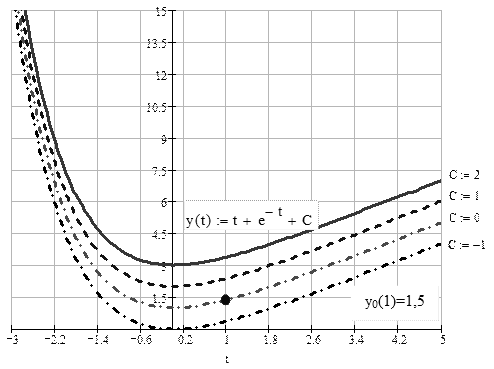

 .
. .
. .
. (8.4)
(8.4) (8.5)
(8.5) (8.6)
(8.6) , можемо помітити, що при досить малому кроці
, можемо помітити, що при досить малому кроці  формула дотичної:
формула дотичної:  . При малих значеннях
. При малих значеннях  обчислена ордината у1(х) наближається до у(х) в точці х1 (рис. 8.2) і чергова точка (х1, у1) може бути вибрана за початкову точку для розрахунку значення функції у(х) на наступному інтервалі [ х1 , х2 ].
обчислена ордината у1(х) наближається до у(х) в точці х1 (рис. 8.2) і чергова точка (х1, у1) може бути вибрана за початкову точку для розрахунку значення функції у(х) на наступному інтервалі [ х1 , х2 ].
 (8.7)
(8.7) .
.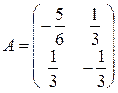 ;
; 
 ;
;  ;
; 


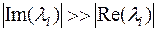 . У цьому випадку явний метод Ейлера застосовувати недоцільно, тому що він нестійкий в області уявної вісі.
. У цьому випадку явний метод Ейлера застосовувати недоцільно, тому що він нестійкий в області уявної вісі. в цій же точці (неявне представлення шуканої величини
в цій же точці (неявне представлення шуканої величини  ) і має вигляд:
) і має вигляд: (8.8)
(8.8) , яка присутня в правій і лівій частинах рівняння. Крок у неявному методі Ейлера обмежений тільки точністю інтегрування. Допустиму похибку апроксимації на крок можемо задати, як
, яка присутня в правій і лівій частинах рівняння. Крок у неявному методі Ейлера обмежений тільки точністю інтегрування. Допустиму похибку апроксимації на крок можемо задати, як  . Після виконання чергового кроку інтегрування розраховується похибка
. Після виконання чергового кроку інтегрування розраховується похибка 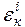 , що повинна бути менше допустимої,
, що повинна бути менше допустимої, (8.9)
(8.9) . Якщо хоча б одне
. Якщо хоча б одне  , то крок зменшується і повторюються розрахунки. Якщо ж
, то крок зменшується і повторюються розрахунки. Якщо ж  для всіх і, то крок розраховується за формулою:
для всіх і, то крок розраховується за формулою:


