Черкаси 2009 6 страница
Також крок можемо вибирати за методом трьох зон:
Остаточно вибирається найменший крок серед всіх значень hi. У формулі (8.11) часто використовують значення m = 2. При жорстких вимогах до точності значення m вибирають більшим.
Приклад 8.2: Розв’яжемо систему звичайних диференційних рівнянь, задану формулою 8.7. 1. Задаємо початкові дані хпоч , хкін , eдоп: х1, 0 = х2, 0 = 0, eдоп = 0, 1. 2. Розрахуємо крок інтегрування за формулою 8.10 чи 8.11. Для початкових ітерацій виберемо його таким як і в попередньому прикладі: h = 0, 3. 3. Розв’яжемо систему відносно хк+1.
4. Виведемо на екран результати. 5. Розрахуємо значення невідомих на перших трьох ітераціях. 6. Після 3-ї ітерації обчислимо
Неявний метод Ейлера може застосовуватися для розв’язання більшості систем звичайних диференційних рівнянь як з малим, так і з великим розсіюванням постійних часу, але трудомісткість кожного кроку значно вище ніж у попередньому методі. Він абсолютно стійкий в області уявної вісі, але дає більш сильне затухання коливальних процесів у порівнянні з реальними коливаннями, тобто має велику похибку розв‘язків [3].
8.4. Модифікації методу Ейлера
Існують різноманітні модифікації методу Ейлера, які спрямовані на уточнення напрямку переходу з точки
Виправлений метод Ейлера. Припустимо, що наближене значення
Якщо обмежитись двома першими елементами в правій частині розкладу (8.12), то отримаємо звичайний метод Ейлера (8.6). Нижче розглянемо, що дає врахування третього доданку. При
Значення першої похідної в точці
Диференціюючи рівняння
знаходимо наближене значення другої похідної:
Підставляючи наближені вирази
Це формула виправленого методу Ейлера. Оскільки при
Удосконалений метод Ейлера називають методом середньої точки, оскільки в ітераційних формулах використовується проміжна точка
Метод Ейлера-Коші (метод Хойна) є одним з варіантів спільного використання методу Ейлера та неявного методу трапецій. В даному методі розрахунки проводяться спочатку за формулою явного методу Ейлера (8.18), а на другому етапі значення функцій усереднюється (формула 8.19):
Геометрична інтерпретація методу полягає у визначенні напрямку інтегральної кривої в точках
Удосконалений метод Ейлера-Коші з ітераційною обробкою. Можна досягти більшої точності, якщо, виходячи з того ж самого початкового наближення
зробити не одну, а кілька ітерацій (як правило k = 3 ¸ 6) за методом трапецій:
Уточнений метод Ейлера. Для отримання наступної модифікації методу Ейлера, проінтегруємо рівняння
звідки отримаємо:
Застосовуючи до останнього інтегралу одноточкову квадратурну формулу середніх прямокутників і замінюючи значення
яку будемо називати уточненим методом Ейлера. Звернемо увагу на одну принципову відмінність методу (8.23) від всіх інших розглянутих до цього моменту методів: уточнений метод є двокроковим. Тут для обчислення значення
8.5. Метод Гюна
Цей метод використовує фундаментальну теорему аналізу, тобто інтегрування функції y¢ (x) на інтервалі [ xk; xk+1 ]:
Якщо з формули (8.24) виразити y(xk+1), то отримаємо формулу (8.22):
Для наближеного обчислення визначеного інтегралу використаємо метод трапецій з кроком h = x1 – x0:
Оскільки рівняння неявне – у правій і лівій частинах є значення
Для обчислення послідовності точок, що є розв‘язком задачі, використовуємо перше наближення за методом Ейлера, позначивши вираз для заміненого
При визначенні похибки остаточний елемент у формулі трапецій, що використовується для наближення інтегралу з формули (8.22), дорівнює
Якщо ми обрахуємо на кожному кроці лише цю похибку, то накопичена похибка на m кроках:
Тобто при зменшенні кроку вдвічі, похибка повинна зменшитися в 4 рази. 8.6. Метод рядів Тейлора
Цей метод є еталонним методом, за яким порівнюють точність різних чисельних методів при розв‘язанні задачі Коші. Теорема Тейлора: Припустимо, що
де інтеграл наближено представлений рядом Тейлора:
У формулі 8.31
де У загальному виді:
де
де
8.7. Методи Рунге-Кутта
Ці методи виводяться з відповідних методів Тейлора таким чином, щоб остаточна загальна помилка методів не перевищувала порядку О(h N). Методи були виведені для того, щоб на кожному кроці виключити необхідність підрахунку похідних вищих порядків. Методи Рунге-Кутта будуються для будь-яких порядків N, що обумовлені точністю. Найчастіше застосовується метод Рунге-Кутта 4-го порядку (N=4). Він дає досить малу помилку при невеликій кількості розрахунків і не складний для програмування. Метод оснований на обчисленні наступного значення за попереднім по формулі:
де k1, k2, k3, k4 – коефіцієнти, що розраховуються за формулами:
Рунге і Кутт отримали систему рівнянь, що має локальну похибку відсікання порядку О(h5):
Отримані 11 рівнянь вміщують 13 змінних, тому для їх розв’язання потрібні 2 додаткові умови. Такими умовами найчастіше є:
За таких умов розв’язками системи рівнянь будуть:
Підставляючи значення (8.38) та (8.39) в початкове рівняння (8.36) отримаємо формулу для стандартного методу Рунге-Кутта 4-го порядку:
де
Рис. 8.3. Наближення інтегралу за методом Рунге-Кутта 4-го порядку.
Накопичена похибка в методі Рунге-Кутта складається з елементарних похибок, що утворюються на кожному кроці. Дана похибка методу розраховується за формулою:
Приклад 8.3. Задана функція y¢ = (x-y)/2 на інтервалі [ 0; 3 ] з початковою умовою у(0)=1. Виберемо крок h = 0, 25. На першій ітерації підрахуємо значення коефіцієнтів f1, f2, f3, f4 і чергове значення y1:
Контрольні питання 1. Що є розв‘язком звичайного диференційного рівняння? 2. Що називається задачею Коші? 3. За яких умов задача Коші має єдиний розв‘язок? 4. Які основні вимоги пред‘являються до чисельних методів розв‘язання диференційних рівнянь? 5. Від чого залежить точність розв‘язання диференційного рівняння? Порівняйте ці складові з переліком похибок чисельного методу з п. 1.3. 6. Від яких критеріїв залежить розрахунок кроку інтегрування? 7. В яких випадках застосовують адаптивний вибір кроку інтегрування? 8. В чому полягає суть явного методу Ейлера? 9. В яких випадках застосовується неявний метод Ейлера і чому? 10. З якою метою розроблені модифікації явного методу Ейлера? 11. За рахунок чого модифікації методу Ейлера дозволяють отримати більш точний результат, ніж при застосуванні явного методу Ейлера? 12. Який метод розв‘язання задачі Коші є базовим для оцінки похибки і чому? 13. В чому полягає суть методу Гюна? 14. В чому полягає перевага методів Рунге-Кутта при розв‘язанні звичайних диференційних рівнянь? 15. В чому полягає суть алгоритму розв‘язання диференційних рівнянь методом Рунге-Кутта 4-го порядку? Розділ 9. Багатокрокові методи розв’язання диференційних рівнянь в частинних похідних
Методи Ейлера, Гюна, Тейлора, Рунге-Кута називаються однокроковими методами, тому що в них використовується лише інформація про значення диференційного рівняння в одній попередній точці для того, щоб обрахувати значення в наступній, тобто лише значення в початковій точці (t 0; y 0) використовується для обчислення значення диференційного рівняння в точці (t 1; y 1), і загалом, щоб обрахувати ук +1 необхідне лише ук. Але після знаходження значень диференційного рівняння в декількох точках можна їх використовувати для отримання більш точних результатів у наступній вузловій точці. Наприклад, для чотирикрокового методу Адамса-Бешфорса-Маултона необхідні значення в точках ук -3, ук -2, ук -1, та ук для обчислення ук +1. У цьому методі значення диференційного рівняння в чотирьох початкових точках, (t 0, y 0), (t 1, y 1), (t 2, y 2) та (t 3, y 3), розраховуються спочатку для подальшої генерації точок {(t k, y k): k Корисною властивістю багатокрокового методу є можливість визначити локальну помилку відсікання (ЛПВ) та ввести корегуючий елемент, який підвищує точність відповіді на кожному кроці. Також можна визначити, чи буде довжина кроку достатньою, щоб отримати значення ук+1 із заданим рівнем точності, або задати більший крок, який виключить непотрібні обрахування і забезпечить необхідну точність розрахунків.
9.1. Метод Адамса-Бешфорса-Маултона Метод прогнозу-корекції Адамса-Бешфорса-Маултона – це багатокроковий метод, виведений із фундаментальної теореми аналізу:
Прогноз використовує наближення поліномом Лагранжа для функції f (t, y (t)), що побудована по точках (tk -3, yk -3), (tk -2, yk -2), (tk -1, yk -1) i (tk, yk). Для функції f (t, y (t)) з формули (9.1), яка інтегрується на інтервалі [ tk, tk +1] прогноз Адамса-Бешфорса, має вигляд
Як будь-який прогноз, він потребує корекції. Коректор отримується аналогічно. А саме, як тільки значення pk +1 обраховано, його використовують для побудови наступного поліному Лагранжа для функції f (t, y (t)), який будується по точкам (tk -2; yk -2), (tk -1; yk -1) (tk; yk) і новій точці (tk +1; yk +1), в якій замість yk +1 використовується прогноз pk +1, тобто функція в точці tk +1; обраховується як f (tk +1, pk +1). Після розрахунку поліному шляхом інтегрування на інтервалі [ tk; tk +1] отримаємо коректор Адамса-Маултона:
Оцінка помилки і корекція. Залишковий елемент формули чисельного інтегрування використовується, щоб отримати і прогноз, і коректор порядку О(h 5). Локальна помилка відсікання для формул (9.2) та (9.3) має вигляд:
для прогнозу) (9.4)
для коректора) (9.5) Припустимо, що h мале і y (5) (t) – майже усталена на інтервалі. Тоді можна виключити члени, що містять похідну 5-го порядку у формулах (9.4) та (9.5). В результаті отримаємо:
Переваги методу прогнозу-корекції Адамса-Бешфорса-Маултона у тому, що формула (9.6) дає наближену оцінку помилки, яку отримуємо при обчисленні значень pk +1 i yk +1, не використовуючи у (5)(t). Коректор (9.3) використовує наближення
Формулу (9.6.) можна використовувати для покращення значень прогнозу. Якщо припустити, що різниця між значеннями прогнозу і корекції на кожному кроці змінюється повільно, то можна підставити
Його значення використовується замість
Формулу (9.6) також можна використовувати для визначення адаптивної довжини кроку. Можливо зменшити довжину кроку, наприклад, до h /2 і збільшити до 2 h. Припустимо ε = 5× 10-6 – критерій відносної похибки, і нехай kε = 10-5 Якщо Якщо Якщо прогноз і корекція значень не дають відповідностей розв‘язків у п’ять значущих цифр, то за формулою (9.9) зменшують довжину кроку. Якщо ж розв‘язки збігаються до семи або більше значущих цифр, то за формулою (9.10) довжина кроку збільшується. Зменшення довжини кроку потребує чотирьох нових початкових значень. Для заміщення значень, яких не вистачає і які ділять інтервали [ tk -2, tk -1] і [ tk -1, tk ] навпіл, використаємо інтерполяцію функції f (t, y (t)) поліномом четвертого ступеню. Нові чотири вузлові точки, tk -3/2, tk -1, tk -1/2 і tk, використовуються в наступних розрахунках. Інтерполяційна формула, необхідна для отримання нових початкових значень (рис. 9.1) для кроку h/2 має вигляд:
Рис. 9.1. Зменшення довжини кроку до h /2.
Набагато простіше збільшити довжину кроку, тоді для розрахунків за одно-кроковим методом потрібно розрахувати сім попередніх точок (рис. 9.2), щоб подвоїти крок.
Рис. 9.2. Збільшення довжини кроку до 2 ∙ h.
9.2. Метод Мілна-Сімпсона Інший розповсюджений метод прогнозу-корекції це метод Мілна-Сімпсона. Його прогноз базується на інтегруванні функції f (t, y (t)) на інтервалі [ tk -3, tk +1]:
Прогноз використовує наближення поліномом Лагранжа для f(t, y(t)), побудоване по точкам (tk -3, fk -3), (tk -2, fk -2), (tk -1, fk -1) та (tk, fk). Інтегруємо його по інтервалу [ tk -3, fk +1] і отримуємо прогноз Мілна:
|

 , (8.10)
, (8.10) (8.11)
(8.11)
 (формула 8.9). Якщо умови точності виконуються
(формула 8.9). Якщо умови точності виконуються  та
та 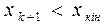 , перейдемо до наступної ітерації з тим же кроком, тобто до п.3. Інакше, якщо
, перейдемо до наступної ітерації з тим же кроком, тобто до п.3. Інакше, якщо  та
та  , розрахуємо новий крок – перейдемо до п.2. Якщо
, розрахуємо новий крок – перейдемо до п.2. Якщо  , припиняємо ітерації.
, припиняємо ітерації. в точку
в точку  . Розглянемо декілька простих модифікацій явного методу Ейлера [17]. Всі наведені нижче методи є методами другого порядку точності, тобто локальна похибка на кожному кроці має порядок
. Розглянемо декілька простих модифікацій явного методу Ейлера [17]. Всі наведені нижче методи є методами другого порядку точності, тобто локальна похибка на кожному кроці має порядок  . Умовою припинення ітерацій для всіх наведених у даному пункті методів є виконання нерівності:
. Умовою припинення ітерацій для всіх наведених у даному пункті методів є виконання нерівності: (8.12)
(8.12) є розв’язком
є розв’язком  задачі Коші й необхідно обчислити
задачі Коші й необхідно обчислити  , де
, де  . Розкладемо розв’язок за формулою Тейлора p -го порядку, приймаючи за базову точку
. Розкладемо розв’язок за формулою Тейлора p -го порядку, приймаючи за базову точку  і покладемо в цьому розкладі
і покладемо в цьому розкладі  . Отримаємо
. Отримаємо (8.12)
(8.12) із (8.12) отримаємо рівняння:
із (8.12) отримаємо рівняння: (8.13)
(8.13) , приблизно відоме:
, приблизно відоме: (8.14)
(8.14) за формулою повної похідної
за формулою повної похідної

 (8.15)
(8.15) ,
,  та
та  в рівність (8.13), отримуємо формулу для обчислення значення функції у наступній точці
в рівність (8.13), отримуємо формулу для обчислення значення функції у наступній точці  при
при  :
: (8.16)
(8.16) формули (8.14) і (8.15) є точними, а
формули (8.14) і (8.15) є точними, а 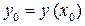 , згідно початкової умови задачі Коші, то на першому кроці обчислення за формулою (8.16) буде виникати похибка, пов’язана тільки з усіканням ряду Тейлора. Тобто, локальна похибка методу (8.16) складає величину
, згідно початкової умови задачі Коші, то на першому кроці обчислення за формулою (8.16) буде виникати похибка, пов’язана тільки з усіканням ряду Тейлора. Тобто, локальна похибка методу (8.16) складає величину  , таким чином виправлений метод Ейлера належить до методів другого порядку.
, таким чином виправлений метод Ейлера належить до методів другого порядку. , яка ділить відрізок між і -ю та (і+1)-ю точкою навпіл. Цим методом розв’язок задачі Коші обчислюється в два етапи за формулами:
, яка ділить відрізок між і -ю та (і+1)-ю точкою навпіл. Цим методом розв’язок задачі Коші обчислюється в два етапи за формулами:
 (8.17)
(8.17) (8.18)
(8.18) (8.19)
(8.19) та
та  , в якості остаточного береться середнє значення цих напрямків.
, в якості остаточного береться середнє значення цих напрямків. (8.20)
(8.20) (8.21)
(8.21) на відрізку
на відрізку  :
: ,
,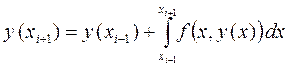 (8.22)
(8.22) і
і  відомими наближеними значеннями
відомими наближеними значеннями  та
та  відповідно, із (8.22) отримаємо формулу для обчислення наближеного значення
відповідно, із (8.22) отримаємо формулу для обчислення наближеного значення  :
: (8.23)
(8.23) використовуються два попередніх значення
використовуються два попередніх значення  та
та  . Двокроковість накладає певні обмеження, принаймні, на початок чисельного процесу: значення
. Двокроковість накладає певні обмеження, принаймні, на початок чисельного процесу: значення  не може бути знайдене безпосередньо за цим методом. Тому недостатню для процесу (8.23) другу початкову точку треба отримувати іншим методом, наприклад, явним методом Ейлера. Так, необхідне значення
не може бути знайдене безпосередньо за цим методом. Тому недостатню для процесу (8.23) другу початкову точку треба отримувати іншим методом, наприклад, явним методом Ейлера. Так, необхідне значення  можна знайти за формулами (8.6) чи (8.17), а потім продовжувати обрахунки за формулою (8.23).
можна знайти за формулами (8.6) чи (8.17), а потім продовжувати обрахунки за формулою (8.23). (8.24)
(8.24)
 (8.25)
(8.25) – для перетворення його у явний вигляд скористаємося формулою Ейлера для
– для перетворення його у явний вигляд скористаємося формулою Ейлера для  , що знаходиться у правій частині рівняння:
, що знаходиться у правій частині рівняння: (8.26)
(8.26) через
через  :
: (8.27)
(8.27) (8.28)
(8.28) (8.29)
(8.29) і що функцію y(x) можна розкласти в ряд Тейлора порядку n у околі фіксованої точки х = хk Î [x0, xn]:
і що функцію y(x) можна розкласти в ряд Тейлора порядку n у околі фіксованої точки х = хk Î [x0, xn]: (8.30)
(8.30) (8.31)
(8.31) є (j-1)-ю похідною по (хk) функції f. Отримаємо формулу для похідної за допомогою рекурентної процедури:
є (j-1)-ю похідною по (хk) функції f. Отримаємо формулу для похідної за допомогою рекурентної процедури: (8.32)
(8.32) є частинними похідними по відповідним змінним.
є частинними похідними по відповідним змінним. (8.33)
(8.33) 3 – диференційний оператор. При розв‘язанні задачі Коші ітерація Тейлора має вигляд:
3 – диференційний оператор. При розв‘язанні задачі Коші ітерація Тейлора має вигляд: (8.34)
(8.34) ,
,  . Остаточна похибка методу Тейлора має порядок
. Остаточна похибка методу Тейлора має порядок  . Точність методу Тейлора залежить від кількості елементів ряду. Для n = 4 і для кроків h та h/2 похибка обчислень:
. Точність методу Тейлора залежить від кількості елементів ряду. Для n = 4 і для кроків h та h/2 похибка обчислень: (8.35)
(8.35) (8.36)
(8.36) (8.37)
(8.37)
 (8.38)
(8.38) (8.39)
(8.39)
 , (8.40)
, (8.40)

 . (8.41)
. (8.41) Всі інші значення на інтервалі [ 0; 3 ] розраховуються аналогічно, не застосовуючи операцію диференціювання.
Всі інші значення на інтервалі [ 0; 3 ] розраховуються аналогічно, не застосовуючи операцію диференціювання. 4} з використанням багатокрокового методу.
4} з використанням багатокрокового методу. . (9.1)
. (9.1)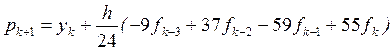 . (9.2)
. (9.2)
 . (9.3)
. (9.3) , (локальна похибка відсікання
, (локальна похибка відсікання . (локальна похибка відсікання
. (локальна похибка відсікання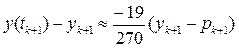 . (9.6)
. (9.6) при обчисленні ук +1. Оскільки ук +1 також є оцінкою для у (tk +1), її можна використовувати у коректорі (9.3) для генерування нового наближення для fk +1, яке, в свою чергу, буде генерувати нове значення для ук +1. Окрім того, якщо продовжити цю ітерацію у коректорі, вона буде збігатись до фіксованої точки у формулі (9.3) швидше, ніж при класичному розв‘язку диференційного рівняння. Якщо необхідно підвищити точність, то процедура корекції більш ефективна, ніж зменшення довжини кроку.
при обчисленні ук +1. Оскільки ук +1 також є оцінкою для у (tk +1), її можна використовувати у коректорі (9.3) для генерування нового наближення для fk +1, яке, в свою чергу, буде генерувати нове значення для ук +1. Окрім того, якщо продовжити цю ітерацію у коректорі, вона буде збігатись до фіксованої точки у формулі (9.3) швидше, ніж при класичному розв‘язку диференційного рівняння. Якщо необхідно підвищити точність, то процедура корекції більш ефективна, ніж зменшення довжини кроку. і
і  замість
замість  і
і  в (9.6) і отримати наступний управляючий параметр:
в (9.6) і отримати наступний управляючий параметр: (9.7)
(9.7) на кроці корекції, і формула (9.3) приймає вигляд:
на кроці корекції, і формула (9.3) приймає вигляд: (9.8)
(9.8) , тоді h = h /2 (9.9)
, тоді h = h /2 (9.9) , тоді h =2 h (9.10)
, тоді h =2 h (9.10) (9.11)
(9.11)

 (9.12)
(9.12)


