Черкаси 2009 8 страница
Умову ортогональності запишемо у вигляді:
звідки отримаємо систему лінійних алгебраїчних рівнянь для знаходження невідомих коефіцієнтів сі. Якщо праву частину рівнянь (10.38) позначити через dk, то отримаємо наступний вираз для їх обчислення:
Коефіцієнти системи рівнянь (10.37) позначимо через змінні і з врахуванням формули (10.35) запишемо:
Перший інтеграл у формулі (10.40) обчислимо по частинах:
При розв‘язанні задачі ми використовуємо (n-1) базисних функцій (10.36), які у точках a і b дорівнюють нулю. Тому можемо записати:
Обчислити коефіцієнти aki можемо за наступною формулою:
(10.43) Для обчислення коефіцієнтів потрібно знайти похідні для фінітних функцій. Диференціюючи (10.37) отримаємо:
Функція відмінна від нуля тільки на інтервалі
Таким чином, матриця 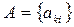 є тридіагональною. є тридіагональною.
Ненульові елементи матриці обчислюються таким чином, для діагональних елементів, для яких
Для елементів правої бічної діагоналі матриці А, для яких
Для елементів лівої бічної діагоналі матриці А, для яких
Дані елементи формують матрицю А системи алгебраїчних рівнянь, що визначаються формулою (10.38), для невідомих коефіцієнтів сі.
10.2.3. Алгоритм методу кінцевих елементів. Метод кінцевих елементів застосовується для розв‘язання систем диференційних рівнянь, що описують певні неперервні процеси у області з довільними границями (рис. 10.4). Алгоритм методу кінцевих елементів складається з наступних етапів: 1) розбиття заданої області на кінцеві елементи, 2) формування апроксимуючої функції кожного елементу, для довільної точки кінцевого елементу апроксимуючий поліном: 3) об‘єднання кінцевих елементів в систему (в ансамбль), на цьому етапі рівняння 4) визначення вектора вузлових значень функції F, існує декілька алгоритмів обчислення даного вектора, одним з яких є мінімізація функціоналу:
1) Виділення кінцевих елементів. Від якості розбиття області на кінцеві елементи переважно залежить точність отриманих результатів. Так, наприклад, розбиття досліджуваної області на двовимірні об‘єкти в формі рівностороннього трикутника, дозволяє отримати результати з меншою похибкою, ніж при розбитті на витягнуті по формі трикутники. В МКЕ за рахунок варіювання розмірами кінцевих елементів можливо більш детально вивчати ті під області об‘єктів, які найбільш насичені факторами впливу (навантаженнями, температурними, електричними, магнітними полями, неоднорідністю властивостей середовища). Розбиття області на кінцеві елементи починається від її границь для найбільш точної форми апроксимації границь. На другому етапі розбивають на елементи внутрішні області. Часто розбиття області на елементи проводять в декілька етапів: 1) область розбивають на досить великі підобласті, границі між якими проходять в місцях змінення фізичних властивостей задачі, геометрії області чи області завантаженості певними факторами, 2) кожну під область розбивають на елементи, при формуванні елементів потрібно уникати різкої зміни розмірів елементів на границях підобласті (розміри елементів повинні змінюватися поступово, як, наприклад, на рис. 10.4). Наступний етап – глобальна (в межах досліджуваної області) нумерація вузлів кінцевих елементів. Вона суттєво впливає на ефективність обчислень. В МКЕ матриця коефіцієнтів системи лінійних алгебраїчних рівнянь є сильно розрідженою матрицею стрічкової структури (рис 10.8). Ненульові елементи цієї матриці розташовані близько головної діагоналі. Ціле число L, що дорівнює найбільшій різниці індексів ненульових елементів в рядку, називається шириною стрічки. Чим менше значення L, тим менший обсяг пам‘яті необхідний для зберігання матриці і тим менші витрати машинного часу на розв‘язання системи ЛАР. Ширина стрічки залежить від числа ступенів свободи і від способу нумерації вузлів. Число ступенів свободи (М) – це кількість невідомих функцій, що визначаються в кожному вузлі. Наприклад, в двовимірній задачі гідравліки у вузлах визначають тиск і складові швидкості по осям Х і У. У такому випадку М = 3. Якщо максимальну різницю між індексами вузлів для окремого елемента позначити через N, то ширину стрічки обчислимо за формулою:
У деяких випадках зменшення величини N досягається послідовною нумерацією вузлів у напрямку найменшого розміру досліджуваної області (рис. 10.9, в). Ширина стрічки при одному ступені свободи дорівнює:
При двох ступенях свободи:
2) Формування апроксимуючої функції. Для визначення апроксимуючої функції найчастіше використовуються поліноми. В залежності від їх ступеню кінцеві елементи поділяються на 1) симплекс-елементи – апроксимуються лінійними поліномами, 2) комплекс-елементи – апроксимуються поліномами, що мають лінійні й нелінійні складові, 3) мультиплекс елементи – вони мають вигляд комплекс-елементів, але на них накладаються додаткові умови: їх границі повинні бути паралельні координатним осям.
Одновимірний симплекс-елемент. Функція j апроксимується поліномом:
Коефіцієнти
Þ
Скориставшись отриманими значеннями коефіцієнтів апроксимуючий поліном запишемо у вигляді:
де Таким чином у підсумку запишемо:
Двовимірний симплекс-елемент. Він може бути представлений у вигляді плоского трикутника з прямолінійними сторонами. Інтерполяційний поліном, що апроксимує неперервну функцію j в межах трикутного симплекс-елементу має вигляд:
Пронумеруємо вузли елементу
При розв‘язанні цієї системи лінійних алгебраїчних рівнянь отримаємо:
де S – площа кінцевого елемента.
У підсумку отримаємо:
де функції форми двовимірного симплекс-елемента:
Аналогічно обчислюються функції інших типів кінцевих елементів. Складаються бібліотеки типових функцій кінцевих елементів.
3) Об‘єднання кінцевих елементів в систему (ансамбль). Суть цього етапу полягає у заміні довільно вибраних номерів вузлів Складемо систему рівнянь для одновимірного об‘єкту, що розбитий на 5 елементів. Функція для кожного елементу має вид:
Запишемо співвідношення між довільними індексами елемент 1 і = 1 j = 2 елемент 2 і = 2 j = 3 елемент 3 і = 3 j = 4 елемент 4 і = 4 j = 5 елемент 5 і = 5 j = 6
При підстановці значень номерів вузлів дискретної моделі у функцію (10.57) кожного елементу отримаємо систему рівнянь:
Слід звернути увагу на особливість - у системі рівнянь При відомих значеннях У матричній формі формула (10.58) виглядатиме так
4) Визначення вектора вузлових значень. Дана задача може вирішуватися кількома методами. Один з методів – мінімізація функціоналу, що пов‘язаний з фізичним сенсом задачі [5, 7].
Контрольні питання 1. Яка задача називається диференційною крайовою задачею? 2. Які умови забезпечують існування єдиного розв‘язку диференційної крайової задачі? 3. Які умови визначають ступінь крайової задачі? 4. В чому полягає суть методів сіток? 5. В яких випадках застосовується метод кінцевих різниць? 6. На чому оснований алгоритм методу кінцевих різниць? 7. Алгоритм методу кінцевих елементів. 8. В чому особливості застосування методу кінцевих елементів? 9. Від яких факторів залежить оптимізація розрахунків за методом кінцевих елементів?
Інтегрована система автоматизації математичних та науково-технічних розрахунків MatLab є добре апробованою надійною системою розв‘язання математичних задач з поданням даних у вигляді матриць. Вона розроблена фірмою MathWorks Inc. При створенні багатьох автоматизованих систем математичних обрахунків розробники прагнули уникнути необхідності написання користувачем власних програмних кодів. Але такий підхід значно обмежував можливості користувача при розв‘язанні задач, що використовують нові методи та алгоритми. Розробники MatLab провели величезну роботу по створенню операторів і функцій для розв‘язання багатьох практичних задач. До таких функцій належать як прості (транспонування матриць, обчислення косинуса та ін.) так і складні функції, що реалізують певні методи розв‘язання задач. Число таких функцій сягає багатьох тисяч і невпинно збільшується. А для вирішення задач з використанням алгоритмів користувача, MatLab має потужну математично-орієнтовану мову програмування високого рівня. Тому інтегрована система автоматизації математичних MatLab з успіхом застосовується в багатьох країнах Європи для розв‘язання нових, нестандартних та найбільш складних математичних задач. Мова програмування в системі MatLab нагадує Паскаль. Запис коду програми відбувається у редакторі системи, що викликається з рядка головного меню MatLab командами File ® New ® M-file, але попередньо може бути написаний у будь-якому текстовому редакторі. Файл коду програми називається m -файлом і має розширення. m, тобто можемо записати: filename.m Система MatLab має власний редактор і відладчик. Формули створюваних методів записуються у формі, притаманній мовам програмування, але ця незручність компенсується високою швидкістю обрахунків, яка, наприклад, на порядок вища ніж у системи MathCad. Мова програмування системи MatLab використовує майже всі відомі засоби програмування, в тому числі об‘єктно-орієнтоване і візуальне програмування, тобто на ній можна створювати повноцінні додатки з розвиненою функціональністю та сучасним інтерфейсом. У програмному коді можна використовувати також внутрішні функції MatLab. Це забезпечує великі можливості при створенні програм як початківцям так і досвідченим програмістам.
В системі MatLab реалізовані два підходи до розв’язання задач: ü з використанням внутрішніх функцій, що реалізовані розробниками MatLab, ü за допомогою написаних користувачем власних програм, код яких формується у вигляді m -файлів.
Для реалізації власних алгоритмів і методів розв‘язання задач скористайтеся редактором і відладчиком, які дозволяють отримати власну функцію для розв‘язання задачі у вигляді m -файлу. При написанні власного коду і роботі над помилками користувач має викликати її у вікні «Command Window» із вказуванням необхідних параметрів, при цьому у рядку «Current Directory» (рис.1) потрібно вказати повний шлях до папки, в якій знаходиться m-файл. Якщо створений m -файл має помилки, то їх зміст і номер рядка з помилкою виводяться у поточному рядку командного вікна. Серед m -файлів розрізняють файли коду та файли-сценарії. У файлах коду міститься програмний код, який може складатися з однієї чи кількох функцій. У файлах–сценаріях послідовно записують значення змінних, імена внутрішніх функцій та m -файлів, які використовуються для розрахунків.
Структура m-файлу-функції може бути представлена так:
function var=f_name(список_параметрів) %Основний коментар %Додатковий коментар Тіло файлу з будь-якими виразами var=вираз
Файли, записані з розширенням.m, можуть бути файлами-сценаріями. Такі файли можуть створюватися для задавання функції, введення даних у вигляді векторів чи матриць, побудови графіків із заданими параметрами і т.і. Всі записані в файлі-сценарії дані можливо вводити і в «Command Window», але форма файлу-сценарію більш компактна і його можна зберегти у вигляді файлу. При виклику такого файлу у «Command Window» за його ім‘ям всі записані в файлі дані виводяться на екран, після чого можемо викликати файл коду, який їх використовує, реалізуючи певний метод обчислень. Файл-сценарій (Script-файл) має наступну структуру:
%Основний коментар %Додатковий коментар Тіло файлу з будь-якими виразами. Наприклад: визначимо функцію: function y = stepfunc(x) y = 1 + x^3/12; При виклику функції у «Command Window» з конкретним значенням змінної х відобразяться наступні записи (буде виведено обчислений результат): » stepfunc(3) ans = 3.2500 Іноді корисним є розрахунок значень функції за допомогою команди feval. У її параметрах функція повинна бути представлена, як рядок: » feval (inline(‘stepfunc’), 3) ans = 3.2500 Матриці в середовищі MatLab. Всі дані, що вводяться в середовищі MatLab інтерпретуються, як матриці. При введенні матриць розділовим знаком між елементами рядка є пробіл, а між самими рядками – крапка з комою. Наприклад: » М = [1 2 3; 4 5 6; 7 8 9] M = 1 2 3 4 5 6 7 8 9 Для вказування певного елементу матриці, користуються індексами: » М (2; 2) ans = Можемо також задавати матриці у вигляді арифметичних виразів: » С = [1+3^2 cos(0.5) sqrt(9)] C = 10 0.8776 3 Задавати матрицю можна як змінну діапазону: » U = 0: 0.5: 3 U = 0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 При використанні її в якості аргументу отримаємо матрицю того ж розміру: » sin(U) ans = 0 0.4794 0.8415 0.9975 0.9093 0.5885 0.1411 В середовищі MatLab є функції для створення матриць з нульовими елементами (їх часто використовують, як матрицю для запису результатів обчислень) і матриць з одиничними елементами, аргументами цих функцій є їх розмір, що задається у вигляді цілих чисел. » W = zeros(4, 4); створення нульової матриці розміром 4 ´ 4. » H = ones(4, 4); створення матриці з одиничними елементами розміром 4 ´ 4. Операції над матрицями. З матрицями в середовищі MatLab можемо проводити наступні операції: + додавання, - віднімання, * добуток (множення), ^ піднесення до степеня, ' транспонування і спряження.
Додаток Б. Пакети прикладних програм інтегрованої системи автоматизації математичних розрахунків MatLab Система MATLAB має на сьогоднішній день 15 реалізацій, 15-а реалізація відома як версія 2008. Розробник системи фірма – MathWorks. Inc., – піклуючись про рейтинг системи, доповнила її сотнями пакетів прикладних програм, що призначені для розв‘язання складних сучасних технічних задач, найбільш розповсюджені з них наведені в таблиці Б1. Система MATLAB з точки зору її розробників пропонується, як мова програмування високого рівня для математичних та науково-технічних обчислень. Вона відобразила в собі не тільки весь досвід розвитку та комп‘ютерної реалізації чисельних методів за останні три десятиліття, а і досвід розвитку математики за всю історію Людства. Система має компілятор, який дозволяє транслювати коди програм, написаних на внутрішній мові MATLAB, в коди мов високого рівня (С, С++, Fortran та ін.) Системою користуються більш ніж 500 000 тисяч легально зареєстрованих користувачів.
|

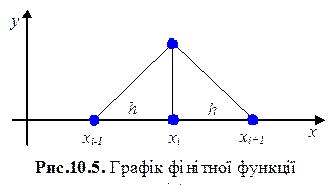 Ці функції називаються фінітними. Графік фінітної функції
Ці функції називаються фінітними. Графік фінітної функції 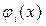 наведений на рис. 10.5., з якого видно, що функція не дорівнює нулю тільки на інтервалі
наведений на рис. 10.5., з якого видно, що функція не дорівнює нулю тільки на інтервалі  . Фінітні функції, що задаються на відрізку
. Фінітні функції, що задаються на відрізку  , лінійно незалежні (і ортогональні в спеціальній енергетичній нормі) і утворюють повну систему в просторі
, лінійно незалежні (і ортогональні в спеціальній енергетичній нормі) і утворюють повну систему в просторі  . Ці властивості є підставою для їх використання в якості базисних функцій в методі Гальоркіна [18].
. Ці властивості є підставою для їх використання в якості базисних функцій в методі Гальоркіна [18].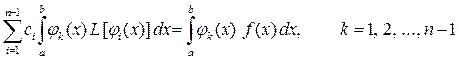 (10.38)
(10.38)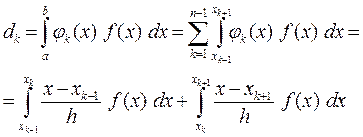 (10.39)
(10.39)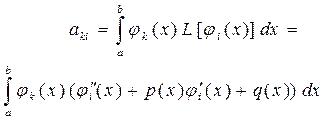 (10.40)
(10.40)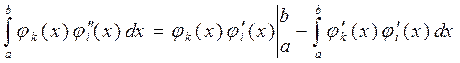 (10.41)
(10.41)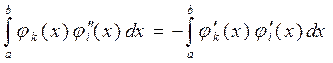 (10.42)
(10.42)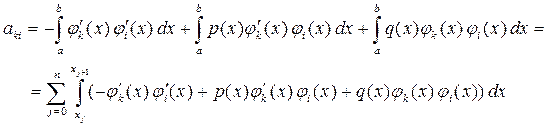
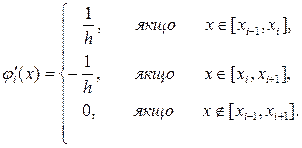 (10.44)
(10.44)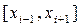 , на якому відмінними від нуля є також фінітні функції і їх похідні (10.37 та 10.44). Тобто добутки
, на якому відмінними від нуля є також фінітні функції і їх похідні (10.37 та 10.44). Тобто добутки 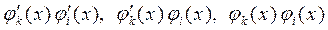 у формулі (10.43) будуть відмінними від нуля тому, що розглядаються значення на інтервалі
у формулі (10.43) будуть відмінними від нуля тому, що розглядаються значення на інтервалі 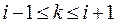 . Але коли
. Але коли 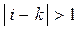 , то
, то 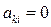 .
. 
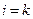 , запишемо:
, запишемо: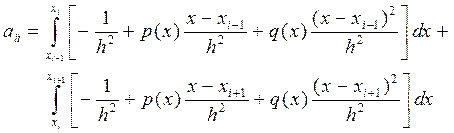 (10.45)
(10.45)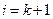 :
: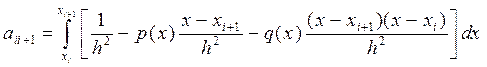 (10.46)
(10.46)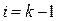 :
: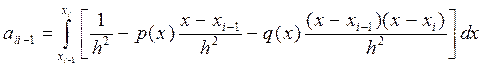 (10.47)
(10.47)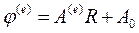 , де
, де 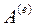 – вектор коефіцієнтів поліному,
– вектор коефіцієнтів поліному, 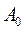 – вектор вільних елементів,
– вектор вільних елементів,  – вектор координат в точці розгляду. Вектор
– вектор координат в точці розгляду. Вектор 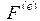 вузлових значень функції і координати вузлів. Після еквівалентних перетворень отримуємо
вузлових значень функції і координати вузлів. Після еквівалентних перетворень отримуємо 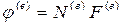 , де
, де 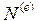 – матриця-рядок, яка складається з функцій форми кінцевого елементу, ці функції визначаються в кожній точці кінцевого елементу через координати самої точки і координати вузлів елементу,
– матриця-рядок, яка складається з функцій форми кінцевого елементу, ці функції визначаються в кожній точці кінцевого елементу через координати самої точки і координати вузлів елементу, , що записані для кожного елементу, об‘єднуються в систему лінійних чи нелінійних алгебраїчних рівнянь виду
, що записані для кожного елементу, об‘єднуються в систему лінійних чи нелінійних алгебраїчних рівнянь виду 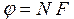 , що є моделлю неперервної функції, яка відображає неперервний процес в досліджуваній області,
, що є моделлю неперервної функції, яка відображає неперервний процес в досліджуваній області,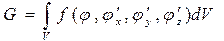 , який відображає фізичний сенс розв‘язуваної задачі.
, який відображає фізичний сенс розв‘язуваної задачі.
 (10.47)
(10.47)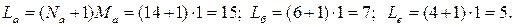
 З прикладу бачимо, що раціональна нумерація вузлів в другому випадку скорочує вдвічі необхідний обсяг оперативної пам‘яті в порівнянні з першим випадком, а у третьому випадку - втричі.
З прикладу бачимо, що раціональна нумерація вузлів в другому випадку скорочує вдвічі необхідний обсяг оперативної пам‘яті в порівнянні з першим випадком, а у третьому випадку - втричі. Рис. 10.9. Варіанти нумерації вузлів кінцевих елементів у криволінійній області.
Рис. 10.9. Варіанти нумерації вузлів кінцевих елементів у криволінійній області.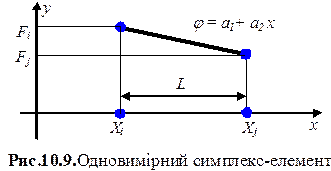
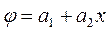 (10.48)
(10.48)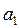 і
і 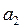 знаходимо через вузлові значення функції
знаходимо через вузлові значення функції 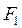 і
і 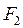 у відповідності до умов неперервності.
у відповідності до умов неперервності.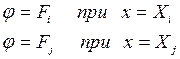 Þ
Þ 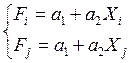 Þ
Þ 
 Þ
Þ 
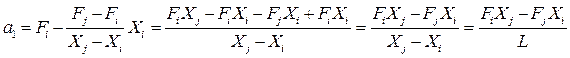
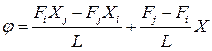 Þ
Þ 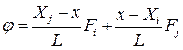 (10.49)
(10.49)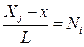 та
та 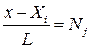 – функції форми одновимірного симплекс-елементу. Функція форми з номером і дорівнює 1 у вузлі з відповідним номером, але дорівнює нулю у всіх інших вузлах.
– функції форми одновимірного симплекс-елементу. Функція форми з номером і дорівнює 1 у вузлі з відповідним номером, але дорівнює нулю у всіх інших вузлах.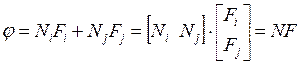 (10.50)
(10.50)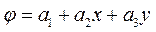 (10.51)
(10.51)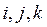 , рухаючись проти часової стрілки. З умови неперервності функції у вузлах отримаємо:
, рухаючись проти часової стрілки. З умови неперервності функції у вузлах отримаємо: (10.52)
(10.52)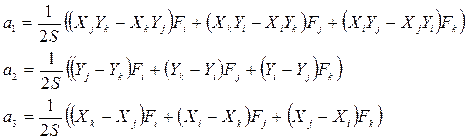 (10.53)
(10.53)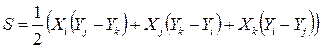 (10.54)
(10.54) (10.55)
(10.55)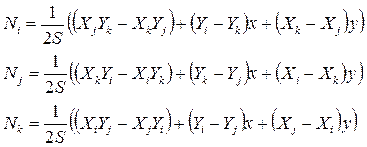 (10.56)
(10.56) (10.57)
(10.57)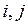 в цьому рівнянні і номерами вузлів в дискретній моделі об‘єкту:
в цьому рівнянні і номерами вузлів в дискретній моделі об‘єкту: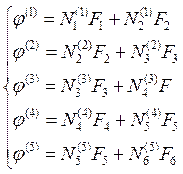 (10.58)
(10.58)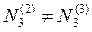 , оскільки
, оскільки 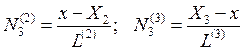 .
.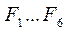 можемо визначити функцію в будь-якій не вузловій точці області.
можемо визначити функцію в будь-якій не вузловій точці області.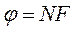 , де
, де (10.59)
(10.59) Щоб скористатися першим способом розв‘язання задач, достатньо задати значення змінної, набрати потрібне ім‘я внутрішньої функції з обов‘язковими параметрами у рядку запрошення вікна «Command Window» і натиснути «Enter» (рис. А1). Якщо у ході розв’язання задачі використовуються кілька методів, то слід викликати їх послідовно, вказуючи необхідні параметри та розділяючи їх крапкою з комою (;). Кожен сеанс роботи в MatLab (у середовищі прийнято іменувати їх сесіями) відображається у вікні «Command Window», він вміщує змінні, значення яких задавалися під час сесії, функції, що викликалися, і всі наслідки «проб і помилок» користувача. Як правило при збереженні сеансу користувача цікавлять лише значення змінних та результати обчислень, їх запам‘ятовують у вигляді mat-файлів з використанням функції save filename. Якщо потрібно записати значення лише одної або кількох змінних, то їх імена вказують наприкінці команди запам‘ятовування, наприклад: save filename X; save filename X Y Z. Якщо ж потрібно зберегти весь сеанс з відображенням всіх функцій, повідомлень про помилки та ін., то користуються функцією diary filename. Всі записані таким чином дані відкриваються у вікні «Command Нistory» (рис. А1).
Щоб скористатися першим способом розв‘язання задач, достатньо задати значення змінної, набрати потрібне ім‘я внутрішньої функції з обов‘язковими параметрами у рядку запрошення вікна «Command Window» і натиснути «Enter» (рис. А1). Якщо у ході розв’язання задачі використовуються кілька методів, то слід викликати їх послідовно, вказуючи необхідні параметри та розділяючи їх крапкою з комою (;). Кожен сеанс роботи в MatLab (у середовищі прийнято іменувати їх сесіями) відображається у вікні «Command Window», він вміщує змінні, значення яких задавалися під час сесії, функції, що викликалися, і всі наслідки «проб і помилок» користувача. Як правило при збереженні сеансу користувача цікавлять лише значення змінних та результати обчислень, їх запам‘ятовують у вигляді mat-файлів з використанням функції save filename. Якщо потрібно записати значення лише одної або кількох змінних, то їх імена вказують наприкінці команди запам‘ятовування, наприклад: save filename X; save filename X Y Z. Якщо ж потрібно зберегти весь сеанс з відображенням всіх функцій, повідомлень про помилки та ін., то користуються функцією diary filename. Всі записані таким чином дані відкриваються у вікні «Command Нistory» (рис. А1).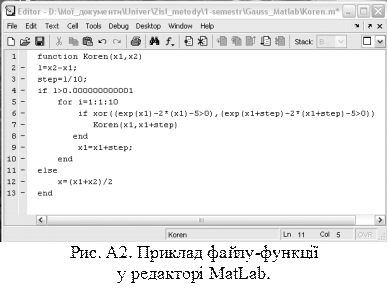 Файли коду. У m -файлі, що містить код, ім‘я вихідної функції повинно співпадати з іменем m -файлу (рис. 2). Внутрішня мова програмування MatLab дуже схожа з мовою програмування Pascal, в ній використовуються ті ж мовні конструкції, відмінності маються лише при зверненні до елементів матриць. Наприклад, якщо потрібно послідовно звертатися до елементів рядка чи стовпчика матриці в MatLab, то на відповідній позиції замість змінної пишуть двокрапку (:), тобто М(і,:). При його створенні та перевірці редактор забезпечує синтаксич ний контроль. Редактор має деякі відладочні можливості – він дозволяє встановити в тексті файлу контрольні точки, в яких призупиняється виконання програми і користувач може оцінити проміжні результати обчислень. Також є можливість покрокового виконання файлу, що особливо важливо при пошуку помилок. Редактор дозволяє зберегти файл в текстовому форматі з розширенням.m
Файли коду. У m -файлі, що містить код, ім‘я вихідної функції повинно співпадати з іменем m -файлу (рис. 2). Внутрішня мова програмування MatLab дуже схожа з мовою програмування Pascal, в ній використовуються ті ж мовні конструкції, відмінності маються лише при зверненні до елементів матриць. Наприклад, якщо потрібно послідовно звертатися до елементів рядка чи стовпчика матриці в MatLab, то на відповідній позиції замість змінної пишуть двокрапку (:), тобто М(і,:). При його створенні та перевірці редактор забезпечує синтаксич ний контроль. Редактор має деякі відладочні можливості – він дозволяє встановити в тексті файлу контрольні точки, в яких призупиняється виконання програми і користувач може оцінити проміжні результати обчислень. Також є можливість покрокового виконання файлу, що особливо важливо при пошуку помилок. Редактор дозволяє зберегти файл в текстовому форматі з розширенням.m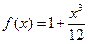 . Файл сценарій запишемо у вигляді:
. Файл сценарій запишемо у вигляді:


