Уравнение прямой на плоскости, различные виды уравненийУгол между прямыми. На координатной плоскости XOY положение прямой определяется углом α, где α – угол наклона прямой к оси OX и отрезком “b”, который они отсекают на оси OY. Чтобы написать уравнение этой прямой, возьмём на ней произвольную точку М (x, y) и найдём соотношение между её координатами (см. рис. 2.1). Из треугольника BMС имеем: 1. Уравнение прямой через данную точку (см. рис. 2.1)
Рис. 2.1
Возьмем на прямой точки M (x, y), M 1(x 1, y 1). Составим треугольник
CM = y – y 1, M 1 C = x – x 1 подставим (1) y – y 1 = k (x – x 1) – уравнение через точку M 1 (см. рис. 2.2). Рис.2.2
2. Уравнение прямой, проходящей через 2 точки М 1 и М 2 можно вывести аналогично из подобия треугольников
Рис. 2.3
3. Общий вид уравнения прямой. Замечаем, что все полученные уравнения обладают тем свойством, что во все уравнения координаты текущей (произвольной) точки M (x, y) входят линейно, т.е. в Все эти уравнения являются частным случаем уравнения вида: Ax + By + C = 0, где A, B, C – произвольные постоянные числа. Построим прямую по её общему уравнению. Задача 2.1: Построить прямую по её общему уравнению
|
или в координатной форме: 
– угловой коэффициент прямой, обозначается k. Отсюда 
или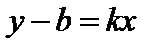 
=> y = kx + b – получили уравнение прямой с угловым коэффициентом.
MM 1 C. Из него получим:
(1).
или
ММ 1 D и 
М 1 М 2 C
или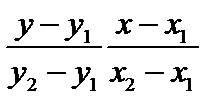 
(см. рис. 2.3).
степени.
