МАТЕМАТИЧЕЧСКАЯ СТАТИСТИКА1) утверждение типа стандартных образцов или типа средств измерений; 2) поверка средств измерений; 3) метрологическая экспертиза; 4) государственный метрологический надзор; 5) аттестация методик (методов) измерений; 6) аккредитация юридических лиц и индивидуальных предпринимателей на выполнение работ и (или) оказание услуг в области обеспечения единства измерений. В законе даны основные понятия, относящиеся к области измерений. Закон устанавливает требования к измерениям, относящимся к сфере гос.регулирования обеспечения единства измерений: - должны выполняться по аттестованным методикам (за исключением методик измерений, предназначенных для выполнения прямых измерений, с применением средств измерений утвержденного типа, прошедших поверку; - результаты измерений должны быть выражены в единицах величин, допущенных к применению в Российской Федерации; - аттестацию методик измерений проводят аккредитованные в установленном порядке в области обеспечения единства измерений юридические лица и индивидуальные предприниматели; - Ростехрегулирование устанавливает порядок аттестации методик и ведет единый перечень измерений, относящихся к сфере государственного регулирования обесп. единства измерений.
Закон устанавливает также требования: - к единицам величин - к эталонам единиц величин - к стандартным образцам - к средствам измерений.
Закон устанавливает работы в области обеспечения единства измерений, которые требуют аккредитации: 1) аттестация методик (методов) измерений, относящихся к сфере государственного регулирования обеспечения единства измерений; 2) испытания стандартных образцов или средств измерений в целях утверждения типа; 3) поверка средств измерений; 4) обязательная метрологическая экспертиза стандартов, продукции, проектной, конструкторской, технологической документации и других объектов, проводимая в случаях, предусмотренных законодательством Российской Федерации.
МАТЕМАТИЧЕЧСКАЯ СТАТИСТИКА Выборочный метод
Для установления закономерностей, которым подчинены случайные события и случайные величины, теория вероятности, как и любая другая наука, обращается к опыту – наблюдениям, измерениям, экспериментам. Результаты наблюдений за случайными величинами объединяются в наборы статистических данных. Задачей математической статистики, раздела современной теории вероятностей, является разработка методов сбора и обработки статистических данных, а также их анализа с целью установления законов распределения наблюдаемых случайных величин [8, 9].
1. Генеральная и выборочная совокупность данных Генеральной совокупностью является набор всех мыслимых статистических данных, при наблюдениях случайной величины:
Наблюдаемая случайная величина Х называется признаком или фактором выборки. Генеральная совокупность есть статистический аналог случайной величины, ее объем N обычно велик, поэтому из нее выбирается часть данных, называемая выборочной совокупностью или просто выборкой
Использование выборки для построения закономерностей, которым подчинена наблюдаемая случайная величина, позволяет избежать ее сплошного (массового) наблюдения, что часто бывает ресурсоемким процессом, а то и просто невозможным. Однако выборка должна удовлетворять следующим основным требованиям: - выборка должна быть представительной, т.е. сохранять в себе пропорции генеральной совокупности, - объем выборки должен быть небольшим, но достаточным для того, чтобы полученные результаты ее анализа обладали необходимой степенью надежности. В табл. 1 приводятся примеры генеральных и выборочных совокупностей. Таблица 1
Отметим, что в более строгом смысле выборку можно представить как многомерную случайную величину
2. Статистическое распределение выборки. Выборочный ряд, полигон, гистограмма и комулянта выборки Возможные значения элементов выборки Упорядоченный по возрастанию значений набор вариант совместно с соответствующими им частотами называется вариационно-частотным рядом выборки:
Ломаная линия, соединяющая точки вариационно-частотного ряда на плоскости Пример 1. Пусть дана выборка полуденных температур месяца мая своим вариационно-частотным рядом, приведенным в табл. 2: Таблица 2
На рис.10.1 приводится полигон частот рассматриваемой выборки.
Рис.10.1 Полигон частот Вариационно-частотный ряд имеет существенный недостаток, а именно, ненаглядность полигона в случае малой повторяемости вариант, например, при наблюдении непрерывного признака его повторяемость в выборке маловероятна. Более общей формой описания элементов выборки, является гистограмма выборки. Для ее построения, разобьем интервал значений выборки
Совокупность интервалов, наблюдаемой в выборке случайной величины и соответствующих им частот, называется гистограммой выборки.
Для частот гистограммы выполнены следующие условия нормировки:
Число интервалов гистограммы m должно быть оптимальным, чтобы, с одной стороны, была достаточной повторяемость интервалов, а с другой стороны не должны сглаживаться особенности выборочной статистики. Рекомендуется значение Пример 2. Наблюдаемые значения полуденной температуры месяца мая разбиты на 6 интервалов, соответствующая гистограмма задана следующей табл. 3: Таблица 3
Гистограмма наблюдаемых температур приводится на рис. 10.2.
Рис. 10.2 Гистограмма частот
Выборочной или эмпирической функцией распределения называется функция
В нашем примере выборочная функция распределения (иногда называемая комулянтой) приводится на рис.10.3. При увеличении объема выборки относительная частота события приближается к вероятности этого события (теорема Бернулли), поэтому выборочная функция распределения
Это утверждение строго доказано и носит форму теоремы Гливенко [7].
Рис. 10.3 Комулянта частот 3. Выборочные характеристики Помимо полигона и гистограммы выборка характеризуется следующими числовыми величинами: Основные характеристики
отклонение (выборочный стандарт).
Дополнительные характеристики
Часто используются моменты 3-го и 4-го порядков в следующей форме:
В статистической практике рассматриваются так же групповые характеристики, например, в интервальных группах гистограммы выборки вычисляются средние интервальные значения и дисперсии.
Пример 3. Рассмотрим вычисление выборочных характеристик для выборки, представленной в примере 1. У этой выборки объема Таблица 4
В последующих столбцах табл. 4, в соответствие с методом сводных таблиц, приводится расчет выборочных моментов и выборочных характеристик через варианты и частоты выборки:
Причем выполняется
Отметим, что все приведенные числовые характеристики являются случайными величинами, поскольку получены по элементам случайно взятой выборки. На элементах другой выборки наблюдений над той же случайной величиной
Выборочные распределения Если наблюдаемая случайная величина
и построим из них случайные величины Пирсона Тогда получим [9, 10]:
Отсюда видно, что случайная величина выборочной дисперсии DВ распределена пропорционально «Хи-квадрат» случайной величине с n степенями свободы, а отклонение выборочного среднего от математического ожидания распределено пропорционально t -величине Стьюдента с n-1 степенью свободы. При сравнении двух выборок объемов n 1 и n2 часто используется случайная величина Фишера со степенями свободы n1 и n2:
1. Распределения Стьюдента и Пирсона Распределения величин
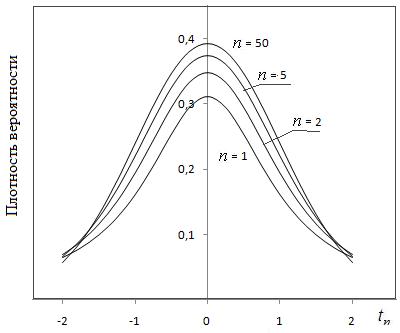
Графический вид функций плотности представлен ниже на рис. 11.1, 11.2 для различного количества степеней свободы.
Рис.11.1 Кривые «Хи-квадрат» распределения
Рис.11.2 Кривые распределения Стьюдента
Числовые характеристики распределений «Хи-квадрат» и Стьюдента следующие:
Можно заметить, что с ростом числа степеней свободы, указанные распределения будут приближаться к нормальному распределению, что соответствует центральной предельной теореме теории вероятностей. 2. Таблицы распределения выборочных величин
Обычно выборочные распределения задаются таблично в виде левосторонних функций распределения
Рис.11.3 Правосторонняя квантиль
В статистическом комплексе программ MS Excel-2007 эти распределения представлены следующими функциями:
Фишера,
Для работы с нормальной случайной величиной имеются следующие полезные функции:
параметрами
Ф
|

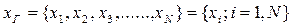 .
.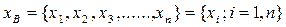 ,
, 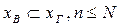 .
.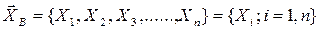 , у которой все компоненты
, у которой все компоненты  распределены одинаково и по закону распределения наблюдаемой случайной величины. В этом смысле выборочные значения
распределены одинаково и по закону распределения наблюдаемой случайной величины. В этом смысле выборочные значения 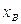 есть одна из реализаций величины
есть одна из реализаций величины  .
.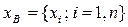 , называются вариантами
, называются вариантами  выборки, причем число вариант m меньше чем объем выборки
выборки, причем число вариант m меньше чем объем выборки  . Варианта может повторяться в выборке несколько раз, число повторения варианты
. Варианта может повторяться в выборке несколько раз, число повторения варианты  . Причем
. Причем  . Величина
. Величина  называется относительной частотой варианты
называется относительной частотой варианты 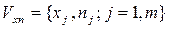 ;
;  .
. или
или 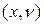 называется полигоном частот.
называется полигоном частот.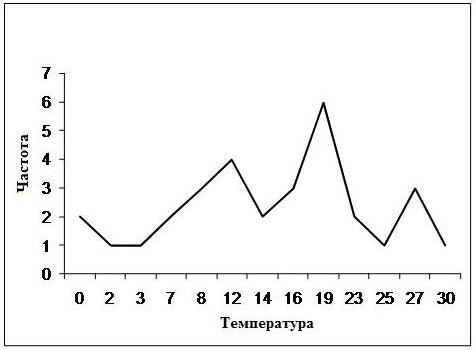
 на m интервалов
на m интервалов  длины
длины 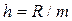 с границами
с границами 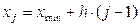 . Число элементов выборки
. Число элементов выборки 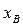 , попадающих в интервал,
, попадающих в интервал,  называется частотой
называется частотой  ~ относительная частота интервала,
~ относительная частота интервала, j ~ плотность относительной частоты интервала.
j ~ плотность относительной частоты интервала.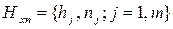 ,
, 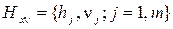 ,
, 
 ,
,  ,
, 
 . На плоскости
. На плоскости 
 , определяющая для каждого значения х относительнуючастоту события { X< x } в выборке, которая вычисляется через сумму соответствующих частот:
, определяющая для каждого значения х относительнуючастоту события { X< x } в выборке, которая вычисляется через сумму соответствующих частот: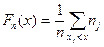 .
.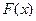 для случайной величины
для случайной величины 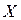 .
. для любого х и
для любого х и 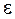
 .
.
 ~ выборочное среднее;
~ выборочное среднее; ~ выборочная дисперсия;
~ выборочная дисперсия; ~ выборочное среднеквадратическое отклонение;
~ выборочное среднеквадратическое отклонение; ~ исправленная выборочная дисперсия;
~ исправленная выборочная дисперсия;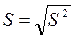 ~ исправленное выборочное среднеквадратическое
~ исправленное выборочное среднеквадратическое ~ выборочный начальный момент порядка k;
~ выборочный начальный момент порядка k; ~ выборочный центральный момент порядка k;
~ выборочный центральный момент порядка k; ~ выборочная асимметрия;
~ выборочная асимметрия;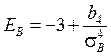 ~ выборочный эксцесс.
~ выборочный эксцесс. имеется m =13 вариант
имеется m =13 вариант  и столько же соответствующих им частот
и столько же соответствующих им частот  , которые расположены в первых двух столбцах табл. 4.
, которые расположены в первых двух столбцах табл. 4.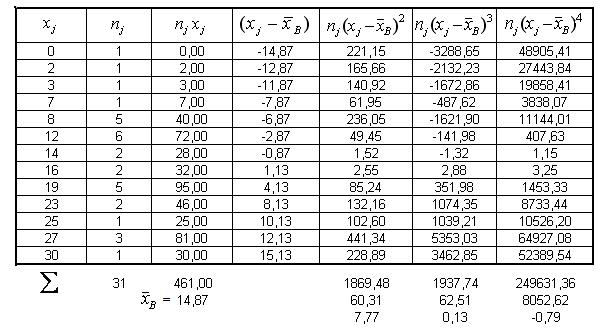
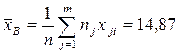 ;
;  ;
;  ;
; ;
; 

 .
. ;
;  ;
;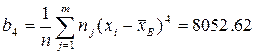 ;
;  .
. числовые характеристики в общем случае изменят свое значение, то есть характеристики являются функцией от выборки
числовые характеристики в общем случае изменят свое значение, то есть характеристики являются функцией от выборки  , например:
, например: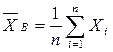 ;
; 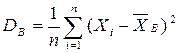 .
.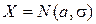 , где
, где 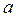 - математическое ожидание,
- математическое ожидание,  - среднеквадратическое отклонение, то случайная величина среднего выборочного
- среднеквадратическое отклонение, то случайная величина среднего выборочного  так же является нормальной
так же является нормальной  . Здесь
. Здесь  нормальные случайные величины, совпадающие с наблюдаемой величиной. Рассмотрим стандартные нормальные величины
нормальные случайные величины, совпадающие с наблюдаемой величиной. Рассмотрим стандартные нормальные величины 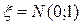 в виде:
в виде: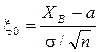 ,
, 
 и Стьюдента
и Стьюдента  .
. ,
, .
. .
.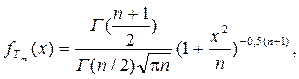
 здесь
здесь  - функция Эйлера, обладающая свойством
- функция Эйлера, обладающая свойством  , в силу которого при целом положительном
, в силу которого при целом положительном  имеет место
имеет место 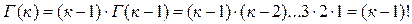

 ,
,  ,
,  ,
,  .
.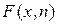 и/или обратных к ним правосторонних квантилей
и/или обратных к ним правосторонних квантилей  , графический смысл которых изображен на рис.11.3. Таблица значений этих величин известна [10] и они приводятся в приложениях 2-5.
, графический смысл которых изображен на рис.11.3. Таблица значений этих величин известна [10] и они приводятся в приложениях 2-5.
 - правостороннее
- правостороннее  распределение Пирсона,
распределение Пирсона, - правосторонняя
- правосторонняя  - правостороннее t -распредел. Стьюдента,
- правостороннее t -распредел. Стьюдента,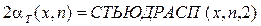 - двухстороннее t –распределение,
- двухстороннее t –распределение,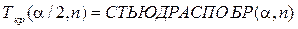 - двухсторонняя t –квантиль,
- двухсторонняя t –квантиль,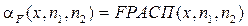 - правостороннее F -распределение
- правостороннее F -распределение FРАСПОБР
FРАСПОБР  - правосторонняя квантиль Фишера.
- правосторонняя квантиль Фишера. - весовая функция
- весовая функция - интегральная функция
- интегральная функция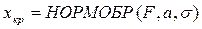 - обратная интегральная функция;
- обратная интегральная функция;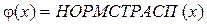 - весовая функция со стандартными
- весовая функция со стандартными
 - обратная стандартная интегральная функция;
- обратная стандартная интегральная функция;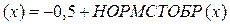 - Функция Лапласа.
- Функция Лапласа.


