Элементы квантовой механикиЭлементы квантовой механики
Для объяснения свойств твердых тел и зависимости этих свойств от атомноэлектронной структуры вещества используются статистические и квантовомеханические представления.
9.1. Дуализм света. Формула Л. де - Бройля
В явлениях интерференции, дифракции, дисперсии, поляризации, поглощения и рассеяния свет проявляет волновые свойства (волновая теория, см. Лекции 1 - 5), т. е. свет - ЭМВ с
В явлениях теплового излучения и фотоэффекта (см. Лекции 6, 7) свет представляет собой поток фотонов (корпускулярная теория) с Таким образом, свет одновременно может проявлять как волновые, так и корпускулярные свойства (дуализм света). Де - Бройль высказал гипотезу: " Дуализм свойственен и другим микрочастицам: электронам, протонам, в отдельных случаях атомам, ионам и т. д. - т. е. имеет универсальную природу". Из гипотезы следует: 1) Дуализм присущ всем микрочастицам (МЧ), не только фотонам. 2) Если существует микрочастица с 3) Соотношения 4) Волны де - Бройля имеют квантовую природу, т. е. вероятностное, статистическое толкование и не имеют аналогов в классической механике. 5) К. Девидссон и Л. Джермер наблюдали дифракцию электронов от Ni - пластины и подтвердили, что как и для рентгеновских лучей (см. Лекция 3), для электронов справедлива формула Вульфа – Бреггов, т. е. 6) Т. Томпсон и Л.В. Тартаковский, изучая спектры электронов и рентгеновских лучей, показали их идентичность, т. е. сделали вывод, что электрон обладает волновыми свойствами. 7) О. Штерн наблюдал дифракцию у атомных и молекулярных пучков. Полученные интерференционные картины оказались идентичны световым. 8) В.А. Фабрикант, Н.Г. Сушкин и Л.М. Биберман, изучая дифракцию электронов, установили, что даже отдельный электрон обладает волновыми свойствами. Этими экспериментами было доказано, что микрочастицы сочетают в себе одновременно корпускулярные и волновые свойства (дуализм). Эти свойства, применительно к электронам, можно сформулировать следующим образом: а) Электрон - это сложное материальное образование со структурой, зависящей от свойств окружающей среды и обладающий волновыми свойствами. б) Корпускулярная природа электрона проявляется в том, что он действует как единое целое, не делясь на части. Итак, качественным отличительным признаком всех микрочастиц является одновременное сочетание в них корпускулярных и волновых свойств, причем волновыми свойствами обладают не совокупность, а каждая из частиц в отдельности.
9.2. Уравнение Шредингера
Качественное отличие микрочастиц от материальных точек, используемых в классической физике, требует и нового подхода к описанию их движения. Так как микрочастица обладает волновыми свойствами, то закон ее движения должен определяться законом распространения соответствующих волн, т. е. волн де - Бройля, и удовлетворять, как и в классической механике, волновому уравнению. Приведем формальный вывод такого уравнения. Пусть плоская волна
Перейдем к новой функции которая связана с волной де - Бройля
и воспользуемся соотношением
Таким образом,
окончательно
Анализ: 1) Как и в классической механике (см. " Механика...". Лекция 7) это дифференциальное уравнение 2-го порядка - есть волновое уравнение. 2) Полученное выражение в квантовой механике называется уравнением Шредингера. 3) Если микрочастица движется в пространстве (
4) Если микрочастица движется в силовом поле, т. е. обладает потенциальной энергией
Во втором слагаемом - Или
Полученное выражение называется полным уравнением Шредингера и описывает движение микрочастицы в силовом поле. 5) Функция 6) Величина 7) Из 6)
8) Уравнение Шредингера можно записать и в виде
9) Уравнение Шредингера в квантовой механике играет ту же роль, что и уравнение второго за - соответствую - кона Ньютона в классической, т. е. – это урав - щего домноже- нение движения микрочастицы. Таким образом, ния левой части задать закон движения микрочастицы означает на задать волновую функцию
9.3. Уравнение Шредингера для стационарных состояний
На практике во многих случаях потенциальная энергия -
т. е. как произведение двух функций, зависящих от разных переменных. Рассмотрим движение микрочастицы вдоль
После подстановки
Разделим переменные, для чего обе части тождества умножим на величину
В этом тождестве левая часть является функцией от времени, а правая - от координаты. Тождество справедливо, если обе части равны const. Пусть const =
Анализ: 1) Для микрочастицы, движущейся в пространстве (объемный случай), или 2) Функции 3) Дифференциальные уравнения для функций 4) Дифференциальное уравнение первого порядка
5) С учетом п. 4.
Найдем После соответствующей подстановки
Вероятность нахождения микрочастицы в объеме 9.4. Соотношение неопределенностей
В классической механике (см. " Механика... ". Лекция 3) было показано, что если материальная точка движется, то: а) Ее состояние однозначно определено с помощью 3-х координат ( б) Существует траектория движения материальной точки. в) Если известна сила г) Для плоского случая (движение материальной точки вдоль оси
Последние соотношения определяют принцип причинности в классической механике, т. е. любое явление имеет причину, его вызывающую. Рассмотрим движение материальной точки при квантовом подходе. Пусть движется (вдоль - Из полученного следует: 1) Из-за двойственной природы микрочастица не имеет одновременно определенных координат и составляющих импульса. В классической механике для материальной точки они определены и в любой момент времени могут быть измерены. 2) Степень точности с какой к микрочастице может быть применено представление о ее определенном положении в пространстве задается соотношениями
которые называются соотношениями неопределенностей или соотношения В. Гейзенберга. Это один из основных законов квантовой механики. 3) Из соотношения неопределенностей следует, что чем точнее определена - координата микрочастицы, тем неопределеннее становится численное значение составляющей импульса и наоборот. 4) В квантовой механике теряет смысл понятие траектории движения, которое нельзя связать с волновыми свойствами микрочастицы. 5) Из соотношения неопределенностей между координатой и составляющей импульса (и наоборот) следует соотношение неопределенностей между энергией и временем
После подстановки
или
Соотношение неопределенностей справедливо и для квантовых систем: " Любая физическая система не может находиться в состояниях, в которых координаты ее центра инерции и импульс одновременно принимают определенные (точные) значения". Математически это можно записать как Из данного определения следует: 1) Ввиду малости величины 2) Никакой эксперимент не может привести к одновременному точному измерению величин 3) Микрочастица из - за двойственной природы при взаимодействиях ведет себя неоднозначно, причем каждое из возможных проявлений осуществляется с определенной степенью вероятности. Система одна, опыты одни и те же, а результаты будут разными, однако, некоторые из результатов наиболее вероятны, т. е. проявляются чаще других. Частота их появления пропорциональна 4) При получении информации об одних величинах теряется информация о других, дополнительных к первым. Это в квантовой механике называется принципом дополнительности. Например, координата - скорость, координата - импульс, кинетическая - потенциальная энергии и т. д. Это объективный принцип квантовых систем. 5) В квантовой механике принцип причинности выражается в уравнении Шредингера, связывающем волновую функцию, зависящую от координат и времени, с величиной силового поля (потенциальной энергией), характеризующей взаимодействие в квантовой системе.
9.5. Движение свободной микрочастицы
Пусть микрочастица движется вдоль
где частицы. После подстановки
Решением данного дифференциального уравнения будет функция Найдем вид функции y (x, y, z, t), которая является решением полного уравнения Шредингера y (x, t) = f (x) j (t) или
После преобразования решение будет иметь вид
Анализ: 1) Решение данной задачи, т. е. волновая функция 2) При движении микрочастицы вдоль положительного направления оси
мости
4) Найдем вероятность нахождения микрочастицы на участке вдоль оси
т. е. вероятность нахождения микрочастицы пропорциональна
|

 и
и .
. или
или  и
и 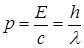 .
. и
и  , то ей соответствует волна с
, то ей соответствует волна с  , которая называется волной де-Бройля.
, которая называется волной де-Бройля. - называются соотношениями де - Бройля.
- называются соотношениями де - Бройля. .
. распространяется вдоль
распространяется вдоль  (плоский случай). Подбором времени пусть a0 = 0, тогда в
(плоский случай). Подбором времени пусть a0 = 0, тогда в комплексной форме
комплексной форме 
 .
. 
 ,
, 
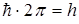
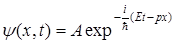

 где
где  - кинетическая энергия,
- кинетическая энергия, 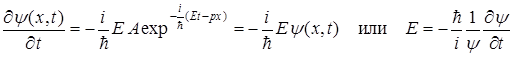

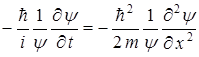
 или с учетом
или с учетом

 ,
,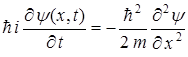 .
. ), то
), то , где D - оператор Лапласа.
, где D - оператор Лапласа. , тогда
, тогда 
 , а волновое уравнение имеет вид:
, а волновое уравнение имеет вид: .
. появляется после домножения обеих частей полученного тождества (см. вывод).
появляется после домножения обеих частей полученного тождества (см. вывод). .
. - являющаяся решением волнового уравнения, называется волновой функцией. Вид ее зависит от характера сил поля, в котором движется микрочастица. Эта функция комплексная, поэтому физический смысл имеет произведение yy*, где y* - комплексно сопряженная функция. В этом случае yy* - есть действительное число.
- являющаяся решением волнового уравнения, называется волновой функцией. Вид ее зависит от характера сил поля, в котором движется микрочастица. Эта функция комплексная, поэтому физический смысл имеет произведение yy*, где y* - комплексно сопряженная функция. В этом случае yy* - есть действительное число.
 - это вероятность того, что микрочастица в любой момент времени находится в выделенном объеме
- это вероятность того, что микрочастица в любой момент времени находится в выделенном объеме  . Так как вероятность не может быть величиной неоднозначной, бесконечной или изменяющейся скачком, то функция
. Так как вероятность не может быть величиной неоднозначной, бесконечной или изменяющейся скачком, то функция  должна быть непрерывной, однозначной, иметь любую производную и конечные значения во всех точках пространства.
должна быть непрерывной, однозначной, иметь любую производную и конечные значения во всех точках пространства. - это условие нормировки. Функция, удовлетворяющая данному уравнению, называется нормированной. С другой стороны, физически данное выражение (условие) означает достоверный факт (вероятность равна единице), что микрочастица находится действительно в выделенном объеме.
- это условие нормировки. Функция, удовлетворяющая данному уравнению, называется нормированной. С другой стороны, физически данное выражение (условие) означает достоверный факт (вероятность равна единице), что микрочастица находится действительно в выделенном объеме.
 После замены
После замены
 не зависит от времени, т. е. силовое поле является стационарным. В этом случае
не зависит от времени, т. е. силовое поле является стационарным. В этом случае  и волновую функцию
и волновую функцию 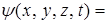

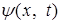 и уравнение имеет вид:
и уравнение имеет вид: .
.
 .
. , тогда
, тогда .
. , где
, где  или
или 
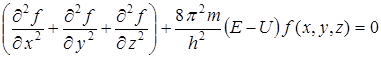
 .
. или
или  , зависящие только от координат, называются амплитудой волновой функции
, зависящие только от координат, называются амплитудой волновой функции 
 имеет решение
имеет решение  , где
, где  - одно из собственных значений энергии.
- одно из собственных значений энергии.


 или
или  .
.  или
или .
.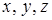 ) и 3-х составляющих импульса (
) и 3-х составляющих импульса ( ), причем в любой момент времени эти величины имеют строго определенные значения и могут быть измерены.
), причем в любой момент времени эти величины имеют строго определенные значения и могут быть измерены.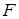 (причина движения), действующая на материальную точку, то можно определить
(причина движения), действующая на материальную точку, то можно определить  для любого
для любого  , т. е. рассчитать все параметры движения, например, ускорение -
, т. е. рассчитать все параметры движения, например, ускорение -  .
.
 или
или 
 . Согласно представлениям де – Бройля такой микрочастице соответствует волна с
. Согласно представлениям де – Бройля такой микрочастице соответствует волна с  , но волна является протяженным объектом (определена -¥ <
, но волна является протяженным объектом (определена -¥ <  < +¥), поэтому интервал Dх, в котором локализована микрочастица с
< +¥), поэтому интервал Dх, в котором локализована микрочастица с  или
или 



 .
.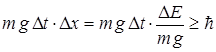

 , т. е. произведение
, т. е. произведение  - не может быть меньше величины порядка
- не может быть меньше величины порядка  .
. и
и  , причем неопределенность связана не с процессом и приборами для измерений, а объективными свойствами материи.
, причем неопределенность связана не с процессом и приборами для измерений, а объективными свойствами материи. и проявляться чаще будут те, которые расположены вблизи максимума волновой функции.
и проявляться чаще будут те, которые расположены вблизи максимума волновой функции. , т. е. она свободная, тогда ее движение описывает амплитудное уравнение Шредингера
, т. е. она свободная, тогда ее движение описывает амплитудное уравнение Шредингера





 и замены
и замены  - волновое число Волновой вектор
- волновое число Волновой вектор .
. 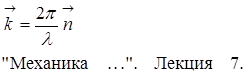



 y(x, y, z, t) = f(x, y, z)j(t)
y(x, y, z, t) = f(x, y, z)j(t)
 .
. - это суперпозиция двух плоских волн, распространяющихся в разных направлениях.
- это суперпозиция двух плоских волн, распространяющихся в разных направлениях. и решением уравнения движения есть функция
и решением уравнения движения есть функция  , т. е. в классической теории (см. " Механика …". Лекция 7) это обычная плоская волна
, т. е. в классической теории (см. " Механика …". Лекция 7) это обычная плоская волна  . В другом случае
. В другом случае  , т. е.
, т. е. 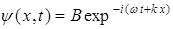 и
и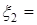
 - тоже плоская волна.
- тоже плоская волна. 3) В процессе вывода получили, что
3) В процессе вывода получили, что  , т. е.
, т. е.  , где
, где  - волновое число. График зависи -
- волновое число. График зависи - .
. ,
, 
 и имеет одинаковое значение вдоль всей траектории движения.
и имеет одинаковое значение вдоль всей траектории движения.


