Если члены знакочередующегося ряда
1) монотонно убывают по абсолютной величине:
2) и стремятся к нулю: то ряд (3) сходится, сумма его S положительна и не превосходит первого члена ряда:
Если знакочередующийся ряд начинается с отрицательного члена:
и для этого ряда выполнены условия 1) и 2) теоремы Лейбница, то и такой ряд сходится, сумма его S отрицательна и удовлетворяет неравенству
Пример 1. Ряд
расходится (гармонический ряд). Таким образом, ряд Лейбница – условно (неабсолютно) сходящийся ряд. Пример 2. Ряд является знакочередующимся. При p > 0 он удовлетворяет условиям признака Лейбница: 1) 2) и, следовательно, сходится. Если заменить все члены их абсолютными величинами, получим ряд Дирихле:
который сходится при p > 1 и расходится при p ≤ 1 (см. §2). Таким образом, ряд (4) при p > 1 сходится абсолютно, а при 0 < p ≤ 1 сходится условно. Пример 3. Доказать сходимость ряда Составим ряд из абсолютных величин членов данного ряда, т. е. ряд
Так как |sin n | ≤ 1, то каждый член ряда (5) не превышает соответствующего члена ряда
Ряд (6) является рядом Дирихле, т. е. рядом вида Пример 4. Сколько членов ряда
нужно взять, чтобы вычислить его сумму с точностью до 0, 001? Данный ряд является знакочередующимся рядом, удовлетворяющим всем условиям признака Лейбница:
Следовательно, данный ряд сходится, притом абсолютно. Чтобы вычислить сумму этого ряда с указанной точностью, необходимо найти такой член, абсолютная величина которого меньше 0, 001, т. е.
то получаем следующую оценку для ошибки:
Пример 5. Исследовать, сходится или расходится ряд
Данный ряд знакочередующийся. Абсолютная величина его общего члена
Поскольку
т. е. общий член ряда к нулю не стремится, ряд расходится (не выполнен необходимый признак сходимости). В заключение темы " Числовые ряды" напомним, какие признаки сходимости можно применять к рядам с положительными членами, и какие – к знакопеременным рядам:
|

 (3)
(3)
 ,
, .
. ,
, .
.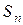 ) абсолютная величина ошибки
) абсолютная величина ошибки  не превышает абсолютного значения первого из отброшенных членов:
не превышает абсолютного значения первого из отброшенных членов:
 .
Знак ошибки (знак
.
Знак ошибки (знак  ) совпадает со знаком первого из отброшенных членов. Здесь
) совпадает со знаком первого из отброшенных членов. Здесь 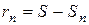 (см. §1).
(см. §1).
 , называемый рядом Лейбница, сходится по признаку Лейбница. В то же время ряд, составленный из абсолютных величин его членов
, называемый рядом Лейбница, сходится по признаку Лейбница. В то же время ряд, составленный из абсолютных величин его членов
 (4)
(4)

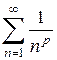 ,
, .
. (5)
(5) (6)
(6)
 .
. или
или  , иначе говоря, n > 10. Следовательно, нужно просуммировать 10 первых членов данного ряда. Так как
, иначе говоря, n > 10. Следовательно, нужно просуммировать 10 первых членов данного ряда. Так как ,
, .
. .
. .
. ,
,


