Сложность алгоритма(пример -подсчета достаточного количества операций)Под сложностью алгоритма понимается количество выполняемых им арифметических операций (сложение, вычитание, умножение, деление). Это определение не учитывает величину чисел участвующих в вычислениях. Ясно, что перемножить два 100-значных числа сложнее чем два однозначных, хотя при этом выполняется лишь одна математическая операция. Поэтому учитывают еще и величину чисел, сводя рассмотрение вопроса к битовым операциям, т.е оценивая количество необходимых операций с 0 и 1 в двоичной записи. Сложность алгоритма представляется функцией от длины входа, т.е от функции количества битов N, требуемых для записи входных данных f(N). Вычислительная сложность алгоритма определяется двумя параметрами: T - временная сложность, S пространственная (требование к памяти). Многие алгоритмы предлагают выбор между объёмом памяти и скоростью. Задачу можно решить быстро, использую большой объём памяти, или медленнее, занимая меньший объём. Величина O - это есть порядок вычислительной сложности, это член разложения функции сложности в ряд быстрее всех растущий с ростом Пример:
Алгоритм называется: Постоянным, если его сложность не зависит от n Линейным, если его временная сложность O(n) Полиномиальным, если его временная сложность O(nm), m=const Экспоненциальным, если O(t f ( N)), где t=const> 1, f(n) - полиномиальная функция от n. сравнений арифметических операций по трудоемкости. Лемма: Пусть n Î N, m Î R - некоторое кольцо. Для вычисления степени Доказательство: Пусть 2S£ n< 2S+1, s=[log2 n] Запишем n в двоичной системе счисления:
Теперь вынесем степени 1, m, m2, …,
|

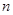 .
.
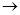

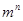 достаточно не более 2[log2 n] умножений.
достаточно не более 2[log2 n] умножений.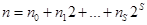
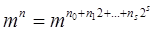
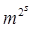 . Всего S операций. Затем перемножаем степени
. Всего S операций. Затем перемножаем степени  , их не более S. В итоге получаем, что для вычисления
, их не более S. В итоге получаем, что для вычисления  .
.


