Решение уравнения Шредингера для простейших случаев
Решение уравнения Шредингера даже для относительно простых реальных объектов, таких как атомы и молекулы, содержащих два и более электронов, изучаемых в теории строения атома и химической связи, представляет собой сложную математическую задачу. Для того чтобы понять характер и особенности результатов квантово-механического описания состояния электрона в атомах и молекулах, решим строго простейшую задачу нахождения электрона в так называемом " потенциальном ящике" – некоторой ограниченной области пространства, вне которой потенциальная энергия электрона обращается в бесконечность. Электрон не может покинуть пределы " потенциального ящика", то есть находится в связанном состоянии. Это, по сути своей, является моделью нахождения электрона в атоме. Электрон в одномерном потенциальном ящике.
Рассмотрим состояние электрона в одномерном потенциальном ящике (рис. 1.3). Движение электрона происходит только вдоль оси X. Внутри ящика потенциальная энергия частицы принимается равной нулю (потенциальную энергию можно отсчитывать от любого выбранного уровня), вне его она равна бесконечности, то есть частица находится внутри ящика и не может покинуть его пределы.
Рис. 1.3. Электрон в одномерном потенциальном ящике: a - параметр (размер) потенциального ящика
С точки зрения классической механики частица, находящаяся в потенциальном ящике, может иметь в принципе любую энергию и находиться в любой точке ящика. При квантово-механическом рассмотрении ситуация меняется. Состояние электрона описывается уравнением Шредингера, и его характеристики (энергия и вероятность нахождения в пространстве) получаются при решении этого уравнения. Как и любое дифференциальное уравнение, уравнение Шредингера имеет бесконечное множество решений. Физический смысл имеют лишь некоторые из них. В нашем случае волновая функция описывает реальную физическую систему, поэтому она должна соответствовать следующим условиям: · конечность – вероятность нахождения электрона в пространстве не может быть больше единицы; · однозначность – вероятность нахождения электрона в точке однозначна; · непрерывность – нет особых точек в пространстве. Волновые функции, удовлетворяющие этим условиям, называются собственными функциями, а соответствующие им значения энергий – собственными значениями энергий. Поскольку электрон находится внутри одномерного «ящика» (V =0), уравнение Шредингера приобретает вид
Известно, что решением данного типа уравнения может быть функция Используя общее решение, граничные условия нашей задачи и принцип нормировки, можно получить волновую функцию, описывающую состояние электрона в потенциальном ящике. Граничными условиями является равенство волновой функции нулю на стенках:
Поскольку амплитуда волновой функции не равна нулю, то из второго условия следует:
Значение амплитуды А находят из условия нормировки. Поскольку электрон находится в потенциальном ящике, то интеграл квадрата волновой функции по координате ящика (от 0 до a) равен единице:
при x =0 и x = a =0
Таким образом, выражение для волновой функции электрона в одномерном потенциальном ящике имеет вид
где a – параметр потенциального ящика; n = 1, 2, 3…– целочисленный параметр. То есть состоянию электрона в потенциальном ящике соответствует набор волновых функций, отличающихся целочисленным параметром n, называемым квантовым числом. Для определения энергии электрона проделаем следующие математические операции. 1. Поскольку в уравнение Шредингера входят волновая функция, и ее вторая производная, запишем их:
2. Подставим выражения волновой функции и ее второй производной в уравнение Шредингера, описывающее состояние электрона внутри потенциального ящика:
3. Поскольку волновая функция внутри ящика не равна нулю: (
То естьнабору волновых функций соответствует набор энергий. Из полученных результатов решения следуют особенности квантово-механического описания состояния электрона в потенциальном ящике. 1. Электрон, находясь в потенциальном ящике, может иметь только дискретные значения полной энергии E 1, E 2, E 3…, величины которых определяет целочисленный параметр n = 1, 2, 3…, называемый квантовым числом. То есть энергия связанного электрона квантована. 2. Распределение вероятности нахождения электрона в объеме потенциального ящика (плотность вероятности) определяется его энергетическим состоянием – энергией, которой обладает электрон.
Графическая интерпретация выводов (рис.1.4). Рис. 1.4. Первое и второе энергетическое состояние электрона в одномерном потенциальном ящике. Полная энергия Еi (1), соответствующая ей волновая функция Y i (x) (2) и плотность вероятности Y i 2(x) (3) электрона
1. Энергия электрона, находящегося в потенциальном ящике, не зависит от координаты и может принимать значения 2. Плотность вероятности для электрона в ящике (распределение вероятности нахождения электрона в различных точках объема) Электрон в трехмерном потенциальном ящике. Вырожденные энергетические состояния. Задача о нахождении частицы в трехмерном потенциальном ящике аналогична предыдущей, их граничные условия полностью совпадают: волновая функция на границах ящика обращается в ноль, потенциальная энергия внутри ящика равна нулю (V =0), а за пределами ящика – бесконечности (V =¥), то есть частица находится в трехмерном потенциальном ящике и не может покинуть его. Единственным отличием является то, что волновая функция для частицы в трехмерном потенциальном ящике является функцией трех пространственных координат: Y(x, y, z). Уравнение Шредингера для данного случая представляет собой дифференциальное уравнение в частных производных с тремя переменными: Стандартным приемом, которым пользуются при решении такого типа уравнений, является разделение переменных: представление волновой функции в виде произведения трех функций, каждая из которых зависит только от одной координаты:
Поскольку правая часть уравнения не зависит от координат, то можно представить полную энергию электрона как сумму трех энергий: E = Ex + + Ey + Ez. Уравнение Шредингера при этом преобразуется в три дифференциальных уравнения, аналогичных волновым уравнениям электрона в одномерном ящике, решение которых уже получено:
Для волновой функции:
a, b, c – параметры трехмерного потенциального ящика (размеры – длина, ширина, высота); nx, ny, nz – целочисленные параметры – «квантовые числа». Необходимо отметить, что каждой координате соответствует свое квантовое число. Для энергии:
Из полученных результатов решения следует:
|


 .
. – общее решение. В принципе вид функции может быть и другим, но она должна быть непрерывной, однозначной и конечной.
– общее решение. В принципе вид функции может быть и другим, но она должна быть непрерывной, однозначной и конечной. ,
, 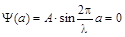 .
.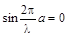 ,
,  , n =1, 2, 3…..,
, n =1, 2, 3…..,  ,
,  .
. ,
,  ,
,  ,
, ,
,  ,
,

 ®
®  .
. ,
, ,
, ,
, .
. ,
, .
. ), то
), то  ,
, , n =1, 2, 3…
, n =1, 2, 3…
 , где a – параметр ящика; m – масса частицы; n – целочисленный параметр.
, где a – параметр ящика; m – масса частицы; n – целочисленный параметр. зависит от энергии частицы.
зависит от энергии частицы. .
. ,
,
 .
.  ,
, ,
, .
. ,
,  ,
,  ,
, ,
, ,
,  ,
,  ,
, .
.


