Теоретическая часть. В числе газообразных и жидких углеводородов по объему их хранения лидирующую позицию занимает, конечноВ числе газообразных и жидких углеводородов по объему их хранения лидирующую позицию занимает, конечно, природный газ. Помимо природного газа в большом количестве резервируются в хранилищах: сырая нефть, сжиженные газы, газовые конденсаты и различные нефтепродукты. В состав природных газов, кроме метана, входят углеводороды до гомологического ряда С5. Существует большой разброс величин физико-химических свойств углеводородов, входящих в состав природных газов. Для составления материальных и тепловых балансов многочисленных процессов, параметров технологического режима хранения и переработки нефти, нефтепродуктов, газообразных углеводородов и их смесей используют понятие компонентного состава. Нефть, нефтепродукты, газообразные углеводороды можно рассматривать как смесь, состоящую из n компонентов. Их число и свойства определяют физико-химическую характеристику смеси в целом. В практических расчётах состав многокомпонентной смеси выражается в долях или процентах. Различают массовые (ω), молярные (х) и объёмные доли (φ):
где ω i – массовая доля i -го компонента; mi – масса i -го компонента;
где хi – молярная доля i -го компонента; ν i – количество вещества i -го компонента; Пересчёт массового состава в молярный и обратный пересчёт осуществляют по формулам:
где Мi – молярная масса i -го компонента.
где Vi –объём i -го компонента; Σ Vi – сумма объёмов n компонентов. К примеру, для газовой смеси состава: ω (С3Н8) = 0, 2; ω (С4Н10) = 0, 8 состав, выраженный в единицах молярных и объёмных долей будет следующим
Для газовых смесей состав, выраженный объёмными и молярными долями, одинаков. Для нефти, нефтяных фракций, нефтепродуктов, газовых смесей углеводородов под понятием «молярная масса» подразумевается её среднее значение, которое находится экспериментально или по эмпирическим зависимостям. Таким образом, учитывая, что располагают газовой смесью, исходя из известного состава и молярных масс компонентов, по правилу аддитивности определяют среднюю молярную массу смеси газов:
где mгаз.см ., nгаз.см. – масса газовой смеси [г, кг] и количество вещества газовой смеси [моль] соответственно; ni – количество вещества i -го компонента газовой смеси [моль], указанного в вариантах задания; Мi – молярная масса i -го компонента смеси [г(кг)/моль(кмоль)], указанного в варианте задания; ω i – массовая доля газа, указанного в вариантах задания (учесть, что Например, для указанной выше газовой смеси:
При этом средняя молярная масса всегда больше, чем наименьшая из молярных масс газов в смеси, и меньше, чем наибольшая молярная масса: Ммин < Mcp < Mмакс. В практике технологических расчётов хранения газовых смесей, а также, например, для определения давления газа при взрыве широко используются законы газового состояния. По сравнению с молекулами жидкости молекулы газов удалены друг от друга на большие расстояния, чем их собственные размеры. С этим связаны некоторые особые свойства газов, например способность к сжатию со значительным изменением объёма, заметное повышение давления с ростом температуры и т.д. Многие реальные газы (углеводородные газы и нефтяные пары) при определенных условиях (невысокие давления и не совсем низкие температуры в малых объёмах, а также высокие давления в больших объёмах) в первом приближении можно рассматривать как идеальные. Поведение газообразных веществ достаточно полно объясняет кинетическая теория газов, основу которой составляют законы газового состояния Бойля-Мариотта, Гей-Люссака, Шарля. Параметры (давление р, объём V, температура T) состояния идеального газа (термодинамические параметры) связывает уравнение Менделеева-Клапейрона. Используя условия задания и вычисленное значение Мср, можно вычислить массу газовой смеси (mгаз.см., [кг]):
где рхр – давление хранения [Па], V [2] – объём газовой смеси (объём резервуара подземного хранилища) [м3], mгаз.см. – общая масса смеси углеводородов [кг], R – универсальная газовая постоянная (8, 314 Дж/(моль·К)), Мср – средняя молярная масса газовой смеси [кг/моль], Tхр – температура хранения углеводородов в подземном хранилище. Для рассматриваемого примера можем рассчитать массу газовой смеси, хранящейся при Тхр = 323 К, рхр = 106 Па в подземном резервуаре объёмом V = 105 м3:
а также массу каждого компонента рассматриваемой смеси газов (С3Н8 и С4Н10)
Для хранения газообразных углеводородов используют сообщающиеся резервуары. Если в двух сообщающихся резервуарах хранятся газовые смеси при разных условиях 1 и 2
то можно определить общую массу газов (m1 + m2) при объединении резервуаров, выражая эту величину из (10) и (11). Так как при объединении двух сообщающихся подземных резервуаров (открыв задвижку) и сохранении требуемого давления, температура газовой смеси Т изменится, то её можно рассчитать, выразив из уравнения (12):
Выразив из уравнения Т3, можно определить температуру газовой смеси, при заданном давлении. Например, имеем резервуар с рассматриваемой газовой смесью при указанных выше условиях и резервуар V = 0, 5·104 м3, в котором находится смесь газов такого же состава, но хранящаяся при Тхр = 303 К и атмосферном давлении. Определим температуру газовой смеси, установившуюся при объединении двух резервуаров с конечным р = 106 Па. Воспользовавшись уравнением (13) с учётом (11) получим:
Закон Бойля-Мариотта гласит, что при постоянной температуре (изотермический процесс) объем данной массы газа (газовой смеси) обратно пропорционален давлению:
при постоянной температуре произведение давления газа на его объем есть величина постоянная: p1·V1 = p2·V2 = const. Учитывая, что плотность газа (ρ) есть отношение его массы (m) к занимаемому объему (V):
можно записать, что
При постоянной температуре давление газа прямо пропорционально его плотности. Используя эти соотношения, можем определить изменение плотности, рассматриваемой в примере газовой смеси, если в подземном резервуаре V = 105 м3 газ находится под буферным давлением рбуф. = 0, 2·106 Па и при температуре хранения Тхр = 323 К, производится закачка газа в резервуар до давления хранения рхр = 106 Па. Используя (17), получаем:
Таким образом, плотность газовой смеси в указанных условиях изменится в 5 раз. Для нефти, нефтепродукта, газообразных углеводородов плотность, как и масса, является важнейшей физической величиной. Плотность газа может быть выражена абсолютным или относительным значением. Абсолютная плотность газа равна его массе в единице объема, в системе СИ она выражается в килограммах на кубический метр (кг/м3). Рассмотрим 2 способа расчёта абсолютной плотности смеси газообразных углеводородов. Так как плотность является аддитивным свойством, то при смешении различных (газообразных, жидких, твёрдых) нефтепродуктов эта величина может быть легко определена. В зависимости от способа выражения состава смеси уравнение выглядит следующим образом:
где mi – масса компонента i смеси, ρ i – плотность i -ого компонента смеси, ω i – массовая доля компонента i в смеси. Если записать уравнение Менделеева-Клапейрона в виде
нетрудно увидеть, что левая часть представляет собой плотность газа (газовой смеси) ρ газ. см., т.е.
Данная формула дает возможность вычислить абсолютную плотность газа (смеси газов) при любых температуре и давлении. Существует другая модификация уравнения Менделеева-Клапейрона, также позволяющая определить плотность газа при любых условиях:
где ρ газ. см. – истинная плотность газовой смеси при условиях, отличных от нормальных (Т, К; р, кПа); ρ о – истинная плотность газовой смеси при н.у. (То = 273 К; ро = 101, 325 кПа). При определении относительной плотности газов и паров нефтепродуктов (D) в качестве стандартного вещества берётся воздух при нормальных условиях (Т = 273 К, р = 101, 325 кПа). Отношение массы газа mгаз.см. к массе воздуха mвозд., взятых в одинаковых объемах и при тех же температуре и давлении, даёт относительную плотность газа:
Плотность любого идеального газа при нормальных условиях равна его молярной массе, отнесённой к объёму, занимаемому 1 моль, т.е.
Определим абсолютную плотность смеси С3Н8 и С4Н10 указанного состава при условиях хранения и относительную плотность газовой смеси при н.у. по воздуху. Для расчётов используем (20), (21) и (23):
Для н.у.
Известно, что ни один термодинамический параметр нельзя изменить, не затронув один или два других параметра, так как все они взаимосвязаны. Такой переход называется изопроцессом. Принципы изменения всех трех термодинамических параметров задает уравнение состояния. Изопроцессы подразделяют на изотермические (Т = const), изохорные (V = const), изобарные (p = const). При изучении изопроцессов получают зависимости (рис. 1), отражающие изменение термодинамических параметров.
Рис. 1. Зависимость между объемом V и давлением р в изопроцессе
Определим, какой изопроцесс изображён на каждом участке графика 1-3, а также изменение термодинамических параметров: - участок 1→ 2: T = const, V уменьшается, р возрастает, что соответствует изотермическому сжатию ( - участок 2→ 3: р = const, V понижается, Т уменьшается, что соответствует изобарному охлаждению; - участок 3→ 1: V = const, p возрастает, Т возрастает, что соответствует изохорному нагреванию ( Схема изменения термодинамических параметров указанного цикла выглядит следующим образом:
Схема 1. Изменение термодинамических параметров
Изобразим зависимость, представленную на рис. 1 в координатах V = f(T) и р = f(T) (рис. 2).
а б Рис. 2. Изопроцесс в координатах V = f(T) – а и р = f(T) – б
Для представления цикла изопроцесса в координатах V = f(m) воспользуемся уравнением (9). Для участков: - 1→ 2: при T = const, m не изменяется, так как T, Mср и R – постоянные, следовательно, m пропорциональна произведению р · V; - 2→ 3: при р = const, m уменьшается; - 3→ 1: при V = const, m возрастает. Таким образом, зависимость приобретает вид:
Рис. 3. Изопроцесс в координатах V = f(m)
Как известно, при горении протекают окислительно-восстановительные реакции. Для определения окислителя и восстановителя в реакции полного сгорания пропана С3Н8 (I) запишем уравнение процесса и определим степени окисления (С.О.) атомов в химических соединениях: C3H8 + O2 → CO2 + H2O (I) Для простых веществ степень окисления принимается равной 0. Поэтому С.О.(О2) = 0. Для СО2 С.О.(С) = +4; С.О.(О) = –2. Для Н2О С.О.(Н) = +1; С.О.(О) = –2.
пропан Таким образом, С.О.(С) = –2; –3 для всех алканов. В молекуле пропана имеется два атома углерода со С.О.(С) = –3 и один атом углерода, проявляющий С.О.(С) = –2: 2С–3 –14ē → 2С+4, С–2 –6ē → С+4 Данные процессы относятся к процессам окисления, а углерод является восстановителем в процессе горения. Восстановитель всегда повышает свою степень окисления. О2 + 4ē → 2О-2 – процесс восстановления; кислород, являющийся составной частью воздуха, является окислителем. Окислитель всегда понижает свою степень окисления. Определим стехиометрические коэффициенты в уравнении химической реакции (I) с учётом одной молекулы углеводорода, участвующей в реакции и используя указанные процессы окисления и восстановления:
2 С–3 + С–2 + 5 О2 –20 ē + 20 ē → 3 С+4 + 10 О–2, получаем C3H8 + 5 O2 → 3 CO2 + 4 H2O. Как правило, окислителем в процессах горения на пожаре является кислород воздуха. Поэтому для решения некоторых практических задач противопожарной защиты необходимо знать количество воздуха, требуемое для полного сгорания единицы количества различных веществ и материалов (определение количества вещества, которое может выгореть до самопроизвольного потухания в замкнутом помещении, содержащем заданный объём воздуха). Для алканов CnH2n+2 стехиометрические коэффициенты в реакции горения в общем виде, будут следующими: CnH2n+2 + (1, 5n+0, 5)O2 → nCO2 + (n + 1)H2O. Для определения объёма воздуха, необходимого для полного сгорания смеси газов при н.у., воспользуемся следующими данными: C3H8 + 5O2 → 3CO2 + 4H2O, (I)
Сухой воздух содержит 21 об.% О2. Следовательно, объём воздуха, содержащий 500, 65·103 м3 кислорода, составит:
Для процесса C4H10 + 6, 5O2 → 4CO2 + 5H2O (II) имеем:
Определение термодинамических функций процессов горения имеет важное практическое значение. Определим тепловые эффекты реакций сгорания углеводородов (I) и (II), в расчете на 1 моль газовой смеси. Запишем термохимические уравнения протекающих реакций: (I) C3H8(г) + 5O2(г) → 3CO2(г) + 4H2O(г) + Δ rHоI (Дж∙ моль–1); (II) C4H10(г) + 6, 5O2(г) → 4CO2(г) + 5H2O(г) + Δ rHоII (Дж∙ моль–1) Воспользуемся справочными данными для необходимых расчётов (табл. 1). Таблица 1 Справочные данные термодинамических функций при 298 К
По следствию из закона Гесса, которое позволяет рассчитывать тепловые эффекты химических реакций, стандартная энтальпия химической реакции
равна разности стандартных энтальпий образования продуктов реакции и реагентов (с учетом стехиометрических коэффициентов):
где Δ r HоТ – изменение энтальпии реакции (тепловой эффект реакции), ν j, ν i – стехиометрические коэффициенты перед формулами конечных и исходных веществ соответственно, Δ f HоТ (Вj) – стандартная энтальпия образования продуктов реакции (конечных веществ), Δ f HоТ (Аi) – стандартная энтальпия образования исходных веществ реакции. Получаем: Δ rHоI, 298 = 3·Δ f Ho298(CО2(г)) + 4·Δ f Ho298(H2O(г)) – (Δ f Ho298(C3Н8 (г)) + 5·Δ f Ho298(О2(г))) = –393, 51·3 + (–241, 82)·4 – (–103, 85 + 5·0) = –2043, 96 (кДж∙ моль–1); Δ rHоII, 298 = 4·Δ f Ho298(CО2(г)) + 5·Δ f Ho298(H2O(г)) – (Δ f Ho298(C4Н10 (г)) + 6, 5·Δ f Ho298(О2(г))) = –393, 51·4 + (–241, 82)·5 – (–126, 15 + 6, 5·0) = –2656, 99 (кДж∙ моль–1). Обе реакции экзотермичны (Δ rHо1, 298, Δ rHо2, 298 < < 0), согласно принципу Бертло-Томсена – самопроизвольны. Учитывая, что х (C3Н8) = 0, 25, х (C4Н10) = 0, 75, рассчитываем тепловые эффекты реакций на 1 моль газовой смеси: Δ rHоI = Δ rHоI, 298 · х (C3Н8) = –2043, 96·0, 25 = -510, 99 (кДж∙ моль–1), Δ rHоII = Δ rHоII, 298 · х (C4Н10) = –2656, 99 ·0, 75 = -1992, 74 (кДж∙ моль–1). Определение изменения энтропии и энергии Гиббса реакций сгорания углеводородов можно произвести также согласно следствию из закона Гесса:
где Δ r SоТ – изменение стандартной энтропии реакции, ν j, ν i – стехиометрические коэффициенты перед формулами конечных и исходных веществ соответственно, SоТ (Вj) – абсолютная энтропия продуктов реакции (конечных веществ), SоТ (А i) – абсолютная энтропия исходных веществ реакции.
где Δ r GоТ – изменение энергии Гиббса реакции, ν j, ν i – стехиометрические коэффициенты перед формулами конечных и исходных веществ соответственно, Δ f GоТ (Вj) – стандартная энергия Гиббса образования продуктов реакции (конечных веществ), Δ f GоТ (А i ) – стандартная энергия Гиббса образования исходных веществ реакции. Получаем: Δ r SoI, 298 = 3·So298(CО2(г)) + 4·So298(H2O(г)) – (So298(C3Н8(г)) + 5·So298(О2(г))) = 3·213, 74 + 4·188, 83 – (269, 91 + 5·205, 138) = 100, 94 (Дж·моль–1·К–1); Δ r SoII, 298 = 4·So298(CО2(г)) + 5·So298(H2O(г)) – (So298(C4Н10(г)) + 6, 5·So298(О2(г))) = 4·213, 74 + 5·188, 83 – (310, 23 + 6, 5·205, 138) = 155, 483 (Дж·моль–1·К–1); D r GоI, 298 = 3·D f Gо298(CО2(г)) + 4·D f Gо298(Н2О(г)) – D f Gо298(C3Н8(г)) – 5·D f Gо298(O2(г)) = 3·(-394, 36) + 4 (–228, 57) – (-23, 49) – 5·0 = –2073, 87 (кДж∙ моль–1); D r GоII, 298 = 4·D f Gо298(CО2(г)) + 5·D f Gо298(Н2О(г)) – D f Gо298(C4Н10(г)) – 6, 5·D f Gо298(O2(г)) = 4·(-394, 36) + 5 (–228, 57) – (-17, 03) – 6, 5·0 = –2703, 26 (кДж∙ моль–1). Δ r SoI, 298, Δ r SoII, 298 > 0, так как увеличивается число молекул газообразных веществ во всех реакциях. D r GоI, 298, D r GоII, 298 < < 0, следовательно, химические процессы термодинамически возможны, т.е. возможно самопроизвольное протекание процессов в прямом направлении.
|

 , (1)
, (1) – сумма масс n компонентов смеси.
– сумма масс n компонентов смеси. , (2)
, (2) – сумма количеств веществ n компонентов смеси.
– сумма количеств веществ n компонентов смеси. (3)
(3) , (4)
, (4) (5)
(5) ,
,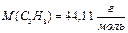
 ,
,
 и
и  ,
, и
и  .
. (6)
(6) , (7)
, (7) , (8)
, (8) ,
,  ).
). .
. , (9)
, (9) ,
, ,
, и
и  ;
; ,
,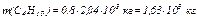 ,
, и (10)
и (10) , (11)
, (11) , (12)
, (12) . (13)
. (13) .
.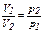 , или (14)
, или (14) , (15)
, (15) или (16)
или (16) . (17)
. (17)
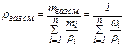 , (18)
, (18)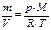 , (19)
, (19) . (20)
. (20) , (21)
, (21) . (22)
. (22) , где ρ газ.см. – плотность газовой смеси при н.у., 22, 4 л – объём 1 моль газа (смеси газов) при н.у. (молярный объём). Тогда для относительной плотности газа (газовой смеси) по воздуху (Dвозд(газ. см.)) можно записать
, где ρ газ.см. – плотность газовой смеси при н.у., 22, 4 л – объём 1 моль газа (смеси газов) при н.у. (молярный объём). Тогда для относительной плотности газа (газовой смеси) по воздуху (Dвозд(газ. см.)) можно записать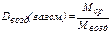 . (23)
. (23)

 из чего следует, что рассматриваемая газовая смесь (С3Н8, С4Н10) при н.у. тяжелее воздуха.
из чего следует, что рассматриваемая газовая смесь (С3Н8, С4Н10) при н.у. тяжелее воздуха.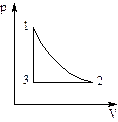
 ,
,  при T2 = T1);
при T2 = T1); , p2 = p3; исключаем V2 и T2 из уравнения, получаем уравнение состояния, описывающее поведение газа изучаемой зависимости
, p2 = p3; исключаем V2 и T2 из уравнения, получаем уравнение состояния, описывающее поведение газа изучаемой зависимости  или
или  ).
).







 , определяем объём воздуха, необходимый для полного сгорания смеси углеводородов:
, определяем объём воздуха, необходимый для полного сгорания смеси углеводородов: .
.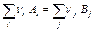 (24)
(24) , (25)
, (25) , (26)
, (26) , (27)
, (27)


