Частные случаи решения уравнений равновесия
1. К телу может быть приложена уравновешенная система параллельных сил (рис. 4.8). Тогда, рационально расположив оси координат (например, ось X – перпендикулярно силам, а ось Y – параллельно им), получим
Рис. 4.8. Уравновешенная система параллельных сил
Если плоская система параллельных сил уравновешена, то алгебраическая сумма проекций сил на ось, параллельную силам, и алгебраическая сумма моментов сил относительно любой точки равны нулю. 2. Расположив центры моментов A и В на прямой, перпендикулярной направлениям сил (рис. 4.9), получим
Рис. 4.9. Уравновешенная система параллельных сил
Если плоская система параллельных сил уравновешена, то равны нулю алгебраические суммы моментов сил относительно двух любых точек, лежащих на прямой, не параллельной линиям действия сил. Для плоской системы параллельных сил можно составить два уравнения равновесия, т. е. для того, чтобы задача могла быть решенной, число неизвестных сил должно быть не больше двух. Вообще говоря, все задачи на равновесие системы сил, в которых число неизвестных не превосходит числа уравнений статики для этой системы, называются статически определимыми. Если же число неизвестных сил превышает число уравнений статики, которые возможно составить для данной системы, то задача называется статически неопределимой.
4.5. Балочные системы. Разновидности опор и виды нагрузок
Объектом решения многих задач статики служат так называемые балки или балочные системы (рис. 4.10). Балкой называется конструктивная деталь какого-либо сооружения, в большинстве случаев выполняемая в виде прямого бруса с опорами в двух (или более) точках. По способу приложения силы условно делятся на сосредоточенные и распределенные.
Жесткая заделка (МА – момент, препятствующий повороту балки)
Рис. 4.10. Балочные системы
Рис. 4.11. Сосредоточенные силы 2. Равномерно распределенная нагрузка (рис. 4.12).
Рис. 4.12. Равномерно распределенная нагрузка
Равномерно распределенная нагрузка задается двумя параметрами – интенсивностью q, т. е. числом единиц силы (Н или кН), приходящихся на единицу длины (м), и длиной l. В задачах статики, где рассматриваются абсолютно недеформируемые (твердые) балки, равномерно распределенную нагрузку можно заменять равнодействующей сосредоточенной силой
4.6. Реальные связи. Трение скольжения и его законы
Если связь идеальная (связь без трения), то ее реакция направлена по нормали к поверхности или к кривой, ограничивающей свободу движения тела (рис. 4.13).
Рис. 4.13. Идеальная связь Если же тело опирается на поверхность реальной связи (связь с трением), то ее реакция отклоняется от нормали на некоторый угол φ (рис. 4.14).
Рис. 4.14. Реальная связь
Таким образом, реакцию реальной связи можно рассматривать как геометрическую сумму составляющих – нормальной
где Постоянное для двух соприкасающихся тел значение
|
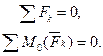
1. Сосредоточенные силы (рис. 4.11). Предполагается, что нагрузка сосредоточена в точке.
.
и касательной 
, которая и есть известная из физики сила трения.
. Угол 
– максимальный угол, на который от нормали к поверхности реальной связи отклоняется ее реакция, называется углом трения:
называется статическим коэффициентом трения (значения коэффициентов трения приводятся в различных физических или технических справочниках) или коэффициентом трения покоя.
