Угловая скорость и угловое ускорение
неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Закон вращательного движения твердого тела вокруг неподвижной оси описывается уравнением
j=f(t),
где j – угол поворота тела. Будем считать угол j положительным, если он отложен в направлении против хода часовой стрелки, и отрицательным, если по ходу часовой стрелки. Измерять угол j будем всегда в радианах. Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость w и угловое ускорение e. Угловая скорость определяется по формуле
Числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак w определяет направление вращения тела: когда вращение происходит против хода часовой стрелки, w> 0, а когда по ходу часовой стрелки, то w< 0. В качестве единицы измерения обычно применяют рад/с или, что то же, 1/с (с–1), так как радиан – величина безразмерная. Угловую скорость тела можно изобразить в виде вектора Численное значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела во времени
Если угловая скорость тела остается во все время движения постоянной (w=const), то вращение тела называется равномерным. В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n (об/мин). Найдем зависимость между n (об/мин) и w (1/с). При одном обороте тело повернется на угол 2p, а при n оборотах на 2pn; этот поворот делается за время t=1 мин=60 с. Тогда
w=p n /30≈ 0, 1 n.
Установив характеристики движения всего тела в целом, перейдем к изучению движения отдельных его точек. 1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис. 17). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время d t происходит элементарный поворот тела на угол dj, то точка М при этом совершает вдоль своей траектории элементарное перемещение d s = h dj. Тогда числовое значение скорости точки будет равно отношению d s к d t, т. е.
угловой скорости тела на расстояние от этой точки до оси вращения. Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М. 2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами a t=d v /d t, аn = v 2/r. В нашем случае r= h. Подставляя значение v в выражения аn и a t, получим
Касательная составляющая ускорения а t направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при замедленном); нормальная составляющая an всегда направлена по радиусу МС к оси вращения (рис. 17). Полное ускорение точки М будет
Основные понятия и определения динамики Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил. Движение тел с чисто геометрической точки зрения рассматривалось в кинематике. В динамике, в отличие от кинематики, при изучении движения тел принимают во внимание как действующие на них силы, так и инертность самих материальных тел. В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений, посвященных изучению движения тел, и проверенные обширной общественно-производственной практикой человечества. Систематически законы динамики были впервые изложены И. Ньютоном в его классическом сочинении «Математические начала натуральной философии», изданном в 1687 г. Сформулировать эти законы можно следующим образом. Первый закон (закон инерции): изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции. Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы, а именно: произведение массы материальной точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлениемсилы. Математически этот закон выражается векторным равенством
При этом между модулями ускорения и силы имеет место зависимость ma = F. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, поскольку при действии данной силы точка, масса которой больше, т. е. более инертная, получит меньшее ускорение и наоборот. Если на точку действует одновременно несколько сил, то они будут эквивалентны одной силе, т. е. равнодействующей
Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны. Этим законом мы уже пользовались в статике. Он играет большую роль в динамике системы материальных точек, как устанавливающий зависимость между действующими на эти точки внутренними силами. При взаимодействии двух свободных материальных точек, они, согласно третьему и второму законам динамики, будут двигаться с ускорениями, обратно пропорциональными их массам. Общие теоремы динамики устанавливают наглядные зависимости между соответствующими динамическими характеристиками движения материальных тел и открывают тем самым новые возможности исследования движения механических систем, широко применяемые в инженерной практике.
|

 Рис. 15
Рис. 15
 .
.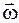 , модуль которого равен |w| и который направлен по оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис. 16). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
, модуль которого равен |w| и который направлен по оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис. 16). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.

 .
Угловое ускорение характеризует изменение с течением времени угловой скорости тела.
Направление
.
Угловое ускорение характеризует изменение с течением времени угловой скорости тела.
Направление  совпадает с направлением
совпадает с направлением  или
v=hw.
Скорость v в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению
или
v=hw.
Скорость v в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению
 Рис. 17
Рис. 17
 ,
,  .
. или
или  .
. .
.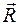 , равной геометрической сумме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид
, равной геометрической сумме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид или
или  .
.


