Частота рекомбинаций хромосом домашней мыши относительно некоторого признака
Фишер (1949) изучал следующие данные, касающиеся частоты рекомбинаций хромосом домашней мыши относительно некоторого признака (т.е. частоты образования гетерозигот). Данные, помещенные в таблице 1, найдены из экспериментов, по возвратному скрещиванию животных. Число, стоящее в знаменателе, равно общему количеству потомков, а в числителе – количеству рекомбинантов, т.е. животных, являющихся гетерозиготами по данному признаку, из общего числа потомков. Задача состоит в том, чтобы получить оценки доли комбинаций хромосом для данных гетерозигот. Таблица 1. Доли рекомбинаций, наблюденные для 20 классов гетерозиготных родителей
Различие по полу. Имеется ли в данных долях рекомбинаций различие по полу для каждого гетерозиготного признака? Рассматривая признак AYAL, мы получаем следующую таблицу.
Критерий независимости χ 2 дает 0, 0905 при одной степени свободы. Сумма значений χ 2 для десяти типов гетерозигот равна 4, 827 при 10 степенях свободы. Вероятность того, что χ 2 при 10 степенях свободы превысит величину 4, 827, очень велика, что указывает на отсутствие различия по полу. Различие между гетерозиготами. Так как в этом случае различиями по полу можно пренебречь, то наблюдения можно собрать в таблицу сопряженности признаков 2 Взаимосвязь между полом и гетерозиготами. Этот пример не совсем удобен для дальнейшего анализа различий по полу. Предположим, мы установили, что существует различие по полу в одном или во всех десяти типах скрещивания. Тогда возникает другая проблема относительно того, будет ли различие по полу одинаково во всех случаях, т.е. необходимо испытать, будет ли существовать взаимосвязь между полом и природой признака. Это можно проверить, используя тригонометрическое преобразование, а затем провести анализ дисперсии. По каждой наблюденной частоте p определяется соответствующий угол φ так, что p = sin2φ. Если величина φ измеряется в градусах, то она имеет дисперсию В таблице 2 приведено 20 значений углов и необходимые вычисления. Значение χ 2 при 10 степенях свободы для испытания различия по полу в каждом из 10 типов равно:
Это немногим больше значения 4, 827, полученного ранее непосредственным применение критерия χ 2. Найдем значение χ 2 при одной степени свободы, которое получается вследствие полного различия по полу во всех типах:
Вычитая теперь это число из величины χ 2 с 10 степенями свободы, получим остаток: 5, 40 – 0, 05 = 5, 35, являющийся значением χ 2 с 9 степенями свободы, которое служит для испытания взаимосвязи между полм и типом гетерозигота. В таком случае можно исследовать различие в типах гетерозигот, проводя суммирование по обоим полам. Однако мы проиллюстрируем соответствующий критерий, считая, что различие по полу существует, но нет взаимодействия. Различия в гетерозиготах, исключая различия по полу. Значения полного критерия χ 2 при 20 – 1 = 19 степенях свободы равно:
Таблица 2. Вычисление взаимосвязи
Таблица 3. Различия в гетерозиготах
При этом суммирование распространяется на все 20 углов. Основные вычисления приведены в таблице 3, где суммирование проведено по всем гетерозиготам. Итоговое значение χ 2 для ♀ и ♂ равно: 10, 17 + 13б40 = 23б57 И имеет 18 степеней свободы. Вычислим компоненту взаимодействия 5, 35 при 9 степенях свободы для испытания различий в гетерозиготах, не включая в рассмотрение пол: 23, 57 – 5, 35 = 18, 22. Полученная величина значима. Этот же результат можно получить несколько отличным путем. Значение χ 2 для пола, когда игнорируют различия в гетерозиготах, получают в следующем виде:
При этом числа взяты из колонок Значение χ 2 для гетерозигот получается при вычитании из общего значения χ 2 величины 0, 01 и суммы квадратов взаимодействия. Это приводит к величине 23, 58 – 0, 01 – 5, 35 = 18, 22, которая совпадает с вычисленной прежде. Таблица 4. Анализ значений χ 2
Суммарное значение χ 2 при 19 степенях свободы значимо, что указывает на общее различие. К полному χ 2 не добавляются различные компоненты χ 2, так как частоты получаются из разных чисел. Источник: http: //www.statsoft.ru/statportal/tabID__50/MId__449/ModeID__0/PageID__361/ DesktopDefault.aspx
Контрольные вопросы: 1. Что такое структура исследования? 2. Дайте характеристику поперечных медицинских исследований. 3. Дайте характеристику продольных медицинских исследований. 4. Что такое ретроспективное и проспективное медицинское исследования? Дайте их характеристики. 5. Перечислите основные биостатистические термины, используемые для представления результатов исследования. 6. Что такое диагностическая чувствительность и диагностическая чувствительность лабораторного теста? Как их рассчитать? 7. Что такое диагностическая эффективность лабораторного теста? Как ее рассчитать? 8. Перечислите возможности систем компьютерной математики. 9. Перечислите основные системы компьютерной математики и укажите их особенности.
Оглавление 1. Структура научно-медицинского исследования с применением медицинской статистики. 3 Статистические термины и показатели, используемые для представления результатов медико-биологических исследований. 9 Проверка нормальности распределения с помощью показателей асимметрии и эксцесса. 10 Практические задания. 15 Приложения. 23 2. Классическое Фрэмингхемское исследование. 28 3. Исследование гемограмм пациентов. 31 Диаграмма рассеяния. 34 Диаграмма Вороного. 37 Описательный (дескриптивный) анализ гемограмм.. 38 Анализ выбросов. 40 Корреляционный анализ. 43 Корреляции Пирсона. 44 Корреляции Спирмена и Кендалла. 45 4. Диагностика остеопороза. 55 Алгоритм вычисления Z-скора (стандартного скора) 56 Алгоритм вычисления Т-скора: 56 5. Частота рекомбинаций хромосом домашней мыши относительно некоторого признака. 57 Контрольные вопросы.. 62
Практикум по медицинской статистике Под редакцией В.В. Решетникова Учебно-методическое пособие по медицинской статистике для студентов 2 курса СПбГПМА Лицензия № 020383 от 14 апреля 1998г. Подписано в печать Формат 60x84/16 Бумага офсетная Гарнитура Times New Roman Объем 4 п.л. Тираж 600 экз. Заказ № Издание ГОУ ВПО СПбГПМА Росздрава.194100, Санкт-Петербург, Литовская ул. дом 2 Отпечатано в ЦМТ СПБГПМА
|




 10. В этом случае одним из качественных признаков естественно считать тип гетерозигот, а другим – природу комбинаций (старая и новая). Критерий однородности χ 2 дает 16, 315 при 9 степенях свободы что является значимым при 5-процентном уровне. Это указывает на различие в рекомбинированных значениях для различных гетерозигот.
10. В этом случае одним из качественных признаков естественно считать тип гетерозигот, а другим – природу комбинаций (старая и новая). Критерий однородности χ 2 дает 16, 315 при 9 степенях свободы что является значимым при 5-процентном уровне. Это указывает на различие в рекомбинированных значениях для различных гетерозигот.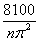 или приблизительно
или приблизительно  .
.





 и
и  таблицы 3.
таблицы 3.



