Решение типовых задач№1. Имеются следующие данные:
Вычислить: 1) индивидуальные индексы цен и количества проданного товара; 2) общий индекс товарооборота; 3) общий индекс физического объема товарооборота; 4) общий индекс цен и сумму экономии или перерасхода от изменения цен; 5) прирост товарооборота за счет изменения цен и количества продажи товаров. Покажите взаимосвязь между исчисленными индексами.
Решение: 1. Индивидуальные индексы (однотоварные): а) цен:
б) количества проданных товаров:
Так, для товара «А» Следовательно, цена на товар А выросла на 25 %.
2. Общий индекс товарооборота исчисляется по формуле:
т.е. товарооборот в отчетном году по сравнению с базисным вырос в 2, 307 раза, или на 130, 7 %. 3. Общий индекс физического объема товарооборота (количества проданных товаров) исчисляется по следующей агрегатной формуле индекса:
Это значит, что количество проданного товара в отчетном периоде было в среднем на 19, 4 % больше, чем в базисном периоде. 4. Общий индекс цен подсчитаем по агрегатной формуле Паше:
т.е. цены на оба товара проданные в отчетном периоде в среднем выросли в 1, 932 раза, или на 93, 2 %. Между исчисленными индексами существует взаимосвязь:
Потери, которые несет население от роста цен в отчетном периоде, исчисляются по данным общего индекса цен Пааше и равны разности между числителем и знаменателем этого индекса:
Следовательно, в связи с ростом цен на 93, 2 % население в отчетном периоде дополнительно израсходовало 9164 тыс. руб. на покупку товаров «А» и «Б». 5. Абсолютный общий прирост товарооборота исчисляется как разность между числителем и знаменателем общего индекса товарооборота:
Этот общий прирост обусловлен изменением цен на товары и изменением количества проданных товаров. Прирост за счет изменения цен составил Следовательно, увеличение товарооборота на 10764 тыс. руб. произошло за счет роста цен на 9164 тыс. руб. и роста количества проданного товара на 1600 тыс. руб. Между исчисленными абсолютными приростами существует взаимосвязь:
№2. Имеются данные о продаже товаров в текущем году:
Вычислить: 1) общий индекс физического объема товарооборота (количества проданных товаров) в декабре к январю; 2) среднее изменение цен по товарным группам, если известно, что товарооборот за этот период вырос в 1, 4 раза.
Решение: 1. Индекс физического объема товарооборота определяется по формуле средневзвешенного арифметического индекса и равен:
Количество продажи товаров в среднем сократилось за год на 32, 5%. 2. Определим среднее изменение цен. Известно, что связь между индексами такая же, как и между соответствующими показателями.
Следовательно, индекс цен равен
№3. Имеются следующие данные:
Определить общий индекс физического объема.
Решение: В данном примере общий индекс физического объема рассчитаем по формуле среднего арифметического индекса:
Это означает, что в целом по всем изделиям выпуск продукции увеличился в среднем на 9, 7 % (109, 7 – 100). Вместо абсолютных данных о стоимости отдельных изделий в базисном периоде можно принимать их доли (удельный вес) в общей стоимости, т.е.
Тогда формула среднего арифметического индекса из индивидуальных будет иметь вид:
Расчет по этой формуле дает тот же результат:
Если
№ 4. Имеются следующие данные по предприятию:
Определить: 1) среднее изменение себестоимости по всем изделиям в июле по сравнению с июнем. 2) как изменился физический объем продукции, если денежные затраты на производство выросли на 1, 6 %.
Решение: 1. Чтобы определить среднее изменение себестоимости по всем изделиям, надо рассчитать индекс себестоимости. По данной информации его можно определить лишь по формуле:
Подсчитаем его:
Среднее увеличение себестоимости всех изделий составило 1, 8 %. 2. Чтобы объяснить, как изменился физический объем продукции, следует рассчитать индекс физического объема продукции. Его определяем, используя взаимосвязь индексов:
Следовательно, физический объем продукции снизился в среднем по изделиям на 0, 2 %. №5. Продажа сельхозпродуктов на рынках города характеризуется следующими данными:
Вычислить: 1) среднее изменение цен на проданные товары; 2) переплату денег от роста цен по каждому товару и по совокупности товаров. Решение: 1. Общий индекс цен равен:
Цены в среднем выросли на 17 % на проданные товары. 2. Переплата денег населения в результате роста цен: по картофелю 90000 – 75000 = 15000 тыс. руб. по моркови 20000 – 15625 = 4375 тыс. руб. по яблокам 230000 – 200000 = 30000 тыс. руб. по совокупности товаров
№6. Имеются следующие данные о производстве продукции и ее себестоимости:
Вычислить: 1) индивидуальные цепные и базисные индексы себестоимости на продукцию «А»; 2) общие цепные и базисные индексы себестоимости и физического объема продукции.
Решение: Цепные и базисные индивидуальные индексы себестоимости: а) цепные:
б) базисные:
Между цепными и базисными индивидуальными индексами существует связь – произведение цепных индексов равно базисному:
Зная базисные индексы, можно вычислить цепные, разделив последующий базисный индекс на предыдущий:
Аналогично исчисляются индивидуальные индексы количества проданных товаров.
3. Исчислим общие индексы себестоимости: а) цепные:
б) базисные:
Как видно из вычислений, цепные качественные общие индексы цен имеют переменные веса на уровне отчетного периода. Для таких индексов нет взаимосвязи между цепными и базисными индексами, что характерно для всех качественных индексов.
Исчислим общие индексы физического объема товарооборота: а) цепные:
б) базисные:
Данные примера показывают, что общие цепные и базисные индексы количественных показателей взвешиваются по постоянным весам, между ними имеется связь: произведение цепных индексов равно базисному:
От базисных индексов можно перейти к цепным, как это показано выше.
№7. Динамика себестоимости и объема продукции «А» на двух предприятиях характеризуется следующими данными:
Вычислите: 1) индекс себестоимости переменного состава; 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов. Покажите взаимосвязь исчисленных индексов.
Решение: 1. Вычислим индекс себестоимости переменного состава, который равен отношению средней себестоимости единицы продукции вида «А» отчетного периода к средней себестоимости единицы продукции базисного периода
Средняя себестоимость единицы продукции вида «А» по двум предприятиям в отчетном и базисном периодах равна:
Следовательно, индекс себестоимости переменного состава равен:
Он показывает, что средняя себестоимость изделия по двум предприятиям выросла на 32, 6 %. Этот рост обусловлен изменением себестоимости продукции по каждому предприятию и изменением структуры выпуска продукции (удельного веса продукции предприятий). Выявим влияние каждого из этих факторов на динамику средней себестоимости, исчислив индекс себестоимости постоянного состава и индекс структурных сдвигов. 2. Индекс себестоимости постоянного состава (индекс фиксированного состава), показывающий, как изменилась средняя себестоимость за счет изменения только себестоимости единицы продукции на предприятиях, равен:
Себестоимость продукции по двум предприятиям в среднем выросла на 34%.
3. Индекс структурных сдвигов, характеризующий степень влияния структурных сдвигов на изменение средней себестоимости единицы продукции, определяется:
или 98, 9%.
Средняя себестоимость изделия в отчетном периоде снизилась на 1, 1% за счет изменения структуры, т.е. за счет увеличения доли продукции второго предприятия с 50 до 60 %, на котором уровень себестоимости продукции был ниже по сравнению с первым предприятием. Исчисленные выше индексы можно вычислять по удельным весам продукции предприятия, выраженным в коэффициентах: а) индекс себестоимости переменного состава –
б) индекс себестоимости постоянного состава –
в) индекс структурных сдвигов –
Индексы переменного состава, постоянного состава и структурных сдвигов взаимосвязаны:
Абсолютное изменение средней себестоимости единицы продукции вида «А» составило: - за счет изменения двух факторов:
-за счет среднего роста собственно себестоимости:
- за счет изменения структуры выпуска продукции:
Взаимосвязь:
Задачи № 6.1 Имеются следующие данные о ценах и продаже товаров на рынке:
Определите агрегатный индекс цен, агрегатный индекс физического объема товарооборота, общий индекс товарооборота. Покажите взаимосвязь индексов.
№ 6.2 Имеются следующие данные о производстве одноименной продукции и ее себестоимости по двум малым предприятиям:
Вычислите: 1) индекс средней себестоимости продукции по двум предприятиям (индекс себестоимости переменного состава); 2) среднее изменение себестоимости продукции по двум предприятиям (индекс постоянного состава); 3) влияние на динамику средней себестоимости изменений в структуре продукции (индекс структурных сдвигов). Поясните полученные результаты и сделайте выводы.
№ 6.3 Себестоимость и объем продукции предприятий характеризуются следующими показателями:
I. Для предприятия 1 (по трем видам изделий) вычислите: 1) общий индекс себестоимости продукции; 2) общий индекс физического объема продукции; 3) общий индекс затрат на продукцию. Покажите взаимосвязь между исчисленными индексами. II. Для двух предприятий вместе (по изделию А-3) вычислите: 1) индекс себестоимости переменного состава (индекс динамики средней себестоимости); 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов. Поясните полученные результаты.
№ 6.4 Имеются следующие данные о продаже товаров в розничной торговле города:
Вычислите: 1) общий индекс физического объема товарооборота в декабре к январю; 2) среднее изменение цен на товары, если известно, что товарооборот в фактических ценах за год вырос в 1, 2 раза.
№ 6.5 По данным статистики продажа товаров на рынках 2-х городов в феврале характеризуется следующими данными:
I. Для города «А» вычислите: 1) общий индекс товарооборота; 2) общий индекс цен на проданные товары (среднее изменение цен); 3) общий индекс физического объема товарооборота (количества проданных товаров). Покажите взаимосвязь исчисленных индексов. Сделайте выводы. II. Для двух городов вместе (по мясу) вычислите: 1) индекс цен переменного состава; 2) индекс цен постоянного состава; 3) индекс структурных сдвигов. Покажите взаимосвязь исчисленных индексов. Сделайте выводы.
№6.6 Имеются следующие данные о продаже товаров в городе:
Вычислите: 1) среднее изменение количества проданных товаров (индекс физического объема товарооборота); 2) среднее изменение цен на проданные товары, если известно, что товарооборот в фактических ценах за прошедший период вырос на 12%.
№ 6.7 Имеются следующие данные:
В IV квартале по сравнению с III кварталом цены на мясные продукты остались без изменения, на молочные продукты повысились на 8 %. Определите средний гармонический индекс цен, индекс физического объема товарооборота, индекс товарооборота. Сделайте выводы. №6.8 Имеются следующие данные о продаже товаров:
Вычислите: 1) общий прирост физического объема товарооборота в отчетном году по сравнению с базисным; 2) индекс цен, если известно, что товарооборот за этот период вырос на 3%.
№ 6.9 Имеются следующие данные о ценах и продаже товаров:
Определите агрегатные индексы цен (базисные и цепные).
№ 6. 10 Как в среднем изменились цены, если известно, что товарооборот вырос на 80%, а физический объем товарооборота снизился на 2%?
№ 6.11 В отчетном году по сравнению с базисным цены на товары в среднем выросли на 8% физический объем продажи товаров вырос в среднем на 12%. Как изменился товарооборот?
№6.12 Затраты на производств чугуна на заводе увеличились на 10% в отчетном периоде по сравнению с базисным. Количество произведенного чугуна снизилось за этот период на 5%. Как изменилась себестоимость чугуна?
№6.13 Индекс физического объема произведенной продукции составил 96, 5%, а индекс цен – 105%. Определите индекс объема производства.
№ 6.14 В мае по сравнению с апрелем физический объем продаж вырос на 6%, в июне по сравнению с маем на 5%. Определите изменение физического объема продаж в июне по сравнению с апрелем. № 6.15 Производственные затраты в отчетном периоде по сравнению с базисным увеличились на 15%. Себестоимость единицы продукции снизилась в среднем на 21%. Определите индекс физического объема продукции.
№ 6.16 Определите индекс средней выработки продукции в расчете на одного рабочего, если объем выпускаемой продукции увеличился на 17%, а численность рабочих сократилась на 2, 5%.
№ 6.17 Выясните как изменилась численность рабочих, если средняя выработка продукции в расчете на одного рабочего возросла на 11%, а объем выпуска продукции вырос с 55 тыс. шт. до 65 тыс. шт.
№ 6.18 Что произошло с ценами на продукцию, если стоимость реализованной продукции за текущий период увеличилась на 16% и количество реализованной продукции за этот период также увеличилось на 16%.
№ 6.19 Определите индекс структурных сдвигов, если известно, что индекс постоянного состава равен 103, 1% а индекс переменного состава 100, 2%.
№ 6.20 Имеются данные по предприятию:
Определите общий индекс физического объема и абсолютное изменение затрат труда вследствие среднего изменения объема выпуска продукции, если на всю продукцию в феврале месяце было затрачено 500 человеко-часов времени.
Тема 7. Статистические методы изучения взаимосвязей социально-экономических явлений
|


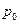
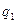
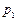
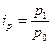 ;
; .
.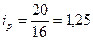 (125 %).
(125 %). (108, 7 %), т.е. количество проданного товара «А» выросло на 8, 7 %. Соответствующие индексы для товара «Б» будут равны
(108, 7 %), т.е. количество проданного товара «А» выросло на 8, 7 %. Соответствующие индексы для товара «Б» будут равны  ;
;  .
.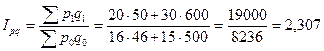 , или 230, 7%,
, или 230, 7%, , или 119, 4%.
, или 119, 4%. , или 193, 2%,
, или 193, 2%, =
=  .
.
 тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. 9164+1600=10764.
9164+1600=10764.
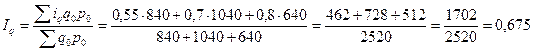 или 67, 5%.
или 67, 5%. ,
, 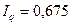 .
.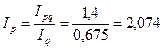 , или 207, 4%. Цены в среднем выросли к концу года в 2, 074 раза.
, или 207, 4%. Цены в среднем выросли к концу года в 2, 074 раза.
 , или 109, 7.
, или 109, 7. , поскольку
, поскольку  .
.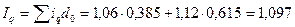 .
. выражены в процентах, формула среднего арифметического индекса будет:
выражены в процентах, формула среднего арифметического индекса будет: .
.
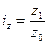
 , где
, где  .
. ; 101, 8%
; 101, 8% ; 99, 8 %.
; 99, 8 %.


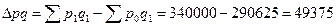 тыс. руб.
тыс. руб. ;
; 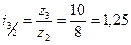 .
. ;
;  .
. .
. .
. , или 152, 9%;
, или 152, 9%; , или 121, 7%;
, или 121, 7%; , или 186, 7%.
, или 186, 7%.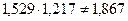
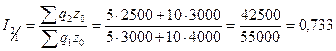 , или 77, 3%;
, или 77, 3%; , или 70, 6%;
, или 70, 6%; , или 54, 5%.
, или 54, 5%.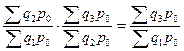 или
или 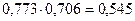

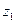
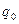

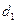
 .
.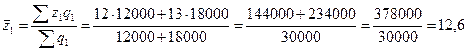 тыс. руб.
тыс. руб. тыс. руб.
тыс. руб. , или 132, 6 %.
, или 132, 6 %.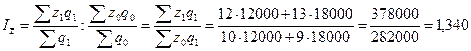 .
. ,
,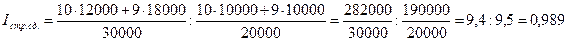 ,
,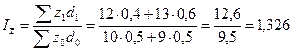 ;
;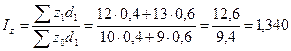 ;
;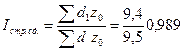 .
.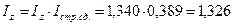 .
. тыс. руб.;
тыс. руб.; тыс. руб.;
тыс. руб.;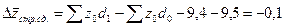 тыс. руб.
тыс. руб.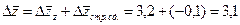 тыс. руб.
тыс. руб.


