Решить задачу линейного программирования Симплекс методом:


1. Составляем первую укороченную симплекс-таблицу СТ1:
| БП СП
| 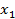
| 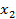
| 
| 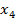
| 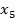
| B
|
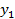
|
|
|
|
|
|
|

|
|
|
|
|
|
|
| Z
| -4
| -10
| -10
| -10
| -12
|
|
Все элементы столбца свободных членов положительные, следовательно, можно применить “Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц”.
2. Выбираем разрешающий столбец l соответствующий наименьшему отрицательному элементу в Z строке:

Следовательно, 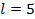
| БП СП
| 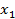
| 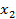
| 
| 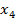
| 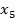
| B
|
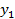
|
|
|
|
|
|
|

|
|
|
|
|
|
|
| Z
| -4
| -10
| -10
| -10
| -12
|
|
3. Выбираем разрешающую строку k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений (элементы столбца B) на соответствующие элементы разрешающего столбца:

Следовательно,  , так как минимальное положительное отношение соответствует первой строке.
, так как минимальное положительное отношение соответствует первой строке.
| БП СП
| 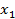
| 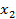
| 
| 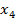
| 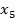
| B
|
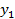
|
|
|
|
|
|
|

|
|
|
|
|
|
|
| Z
| -4
| -10
| -10
| -10
| -12
|
|
- Элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом:

- Переходим к новой симплекс таблице СТ2 по следующим правилам:
- Меняем местами СП и БП соответствующие разрешающему элементу.
- На месте разрешающего элемента в новой таблице стоит величина ему обратная:

- Все элементы разрешающей строки делятся на разрешающее число, включая элемент последнего столбца:
- Все элементы разрешающего столбца делятся на разрешающее число, включая элемент последней строки, с обратным знаком:
- Все остальные элементы матрицы
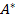 вычисляются по формулам:
вычисляются по формулам:
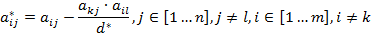
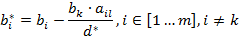
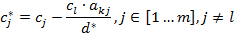
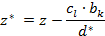
Например, вычислим некоторые элементы таблицы:







Полученная СТ2 следующая:
- В Z строке есть отрицательные элементы, следовательно оптимальное решение не найдено и необходимо выполнить симплекс преобразование для СТ2
- Рассмотрим СТ2:
8. Выбираем разрешающий столбец l, соответствующий наименьшему отрицательному элементу в Z строке:

Следовательно,  .
.
9. Выбираем разрешающую строку k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений (элементы столбца B) на соответствующие элементы разрешающего столбца:

Следовательно,  , так как минимальное положительное отношение соответствует второй строке.
, так как минимальное положительное отношение соответствует второй строке.
10. Элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом: 
- Переходим к новой симплекс таблице СТ2 по следующим правилам:
- Меняем местами СП и БП соответствующие разрешающему элементу.
- На месте разрешающего элемента в новой таблице стоит величина ему обратная:

- Все элементы разрешающей строки делятся на разрешающее число, включая элемент последнего столбца:
- Все элементы разрешающего столбца делятся на разрешающее число, включая элемент последней строки, с обратным знаком:
- Все остальные элементы матрицы
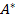 вычисляются по формулам:
вычисляются по формулам:
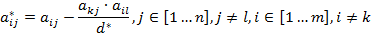
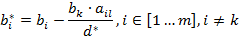
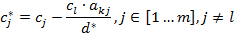
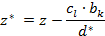
Например, вычислим некоторые элементы таблицы:







Полученная СТ2 следующая:
12. В Z строке нет отрицательных элементов, следовательно, оптимальное решение найдено и максимум целевой функции  для заданной системы ограничений равен 20 при этом
для заданной системы ограничений равен 20 при этом  ,
,  (см столбце свободных членов).
(см столбце свободных членов).
13. Также необходимо определить при каких значениях  достигается максимум целевой функции. Для этого необходимо решить следующую систему уравнений:
достигается максимум целевой функции. Для этого необходимо решить следующую систему уравнений:



Данная система имеет решение только при 
Ответ: Zmax=20  ,
,  ,
, 



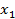
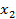

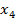
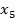
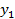


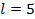

 , так как минимальное положительное отношение соответствует первой строке.
, так как минимальное положительное отношение соответствует первой строке.



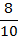



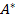 вычисляются по формулам:
вычисляются по формулам: 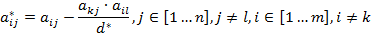
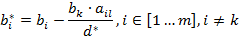
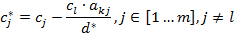
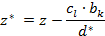
















 .
.
 , так как минимальное положительное отношение соответствует второй строке.
, так как минимальное положительное отношение соответствует второй строке.


















 для заданной системы ограничений равен 20 при этом
для заданной системы ограничений равен 20 при этом  ,
,  (см столбце свободных членов).
(см столбце свободных членов). достигается максимум целевой функции. Для этого необходимо решить следующую систему уравнений:
достигается максимум целевой функции. Для этого необходимо решить следующую систему уравнений:



 ,
, 



