Спектральный анализ
Аномальный эффект может быть также выделен и с помощью фильтрации, о которой речь пойдет позднее. Для процесса фильтрации необходима частотная характеристика как полезного сигнала, так и помехи. Получить такую характеристику помогает спектральный анализ. Чтобы определить частотный диапазон для процесса фильтрации, необходимо определить частоты, на которых амплитуда полезного сигнала начинает превышать амплитуду сигнала-помехи. Для решения этой задачи необходимо рассчитать амплитудно-частотные спектры полезного сигнала и сигнала-помехи. В качестве полезного сигнала в нашем случае выступает модельный сигнал, рассчитанный в работе 3, а в качестве сигнала-помехи – результат пятиточечного сглаживания, полученный в работе 1. Сигналы бывают непрерывными и дискретными. В данном случае сигналы дискретны, так как их функции описываются не уравнением, а набором отдельных значений. Это связано с тем, что исходный сигнал также представляет собой набор отдельных значений магнитного поля в различных точках. Каждый спектр состоит из двух частей: действительной – А и мнимой – В. Рассчитать действительную часть спектра дискретного сигнала можно по формуле:
Рассчитать мнимую часть спектра дискретного сигнала можно по формуле:
В этих выражениях Fi – значение функции в конкретной i-ой точке, х – координата i-ой точки, n – номер гармоники, изменяющийся от 1 до N/2, N – общее количество значений функции. После получения значений действительной и мнимой частей, можно рассчитать непосредственно амплитудно-частотные спектры сигнала и помехи по следующей формуле:
Полученные в результате расчета спектры полезного сигнала и сигнала-помехи значительно отличаются по своей амплитуде, что усложняет, а в некоторых случаях делает практически невозможным их сравнение. Для того, чтобы такое сравнение было возможным, необходимо произвести нормировку обоих спектров на их максимальное значение и произвести построение спектров в единой системе координат как показано на рисунке 12.
Рис. 12 Из рисунка видно, что спектр полезного сигнала, обозначенный красной линией, превышает спектр сигнала-помехи в интервале с 15-ой по 17-ую гармоники (номера гармоник отложены на горизонтальной оси). В случае присутствия нескольких превышений, необходимо ориентироваться на главный максимум спектров. После этого необходимо выбрать полосу частот для расчета фильтрующей функции. Поскольку каждая гармоника соответствут определенной частоте, нужно выписать номера гармоник, которые будут определять полосу пропускания будущего фильтра, при этом номера гармоник могут оказаться дробными. Выбирать гармоники следуе последовательно в направлении увеличения их номера: первое значение – номер гармоники, на которой главный спектр полезного сигнала начинает превышать по амплитуде спектр помехи; второе и третье – на уровне пересечения лини 0, 8 максимума амплитуды и спектра полезного сигнала; четвертое значение – номер гармоники, на которой спектр полезного сигнала перестает превышать по амплитуде спектр помехи.
Задание.
1. Используя данные ранее выполненных работ, рассчитать аплитудно-частотные спектры модельного и наблюденного сигнала. 2. Произвести их нормирование. 3. Определить четыре номера гармоники, определяющие полосу пропускания фильтра. Лабораторная 6.
|

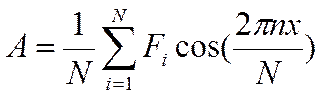 [16].
[16]. [17].
[17].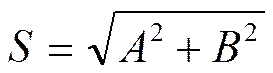 [18].
[18].



