Частные производные функции многих переменных
Приращение функции по одной переменной, при условии, что остальные переменные остаются постоянными, называются частными приращениями.
Если существуют пределы отношений частных приращений функций
При нахождении частной производной по одной переменной, остальные переменные считаются постоянными.
Пример 155 Найти Решение
Пример 156 Найти Решение Пример 157 Найти
Решение
Пример 158 Вычислить значения частных производных функции Решение
Пример 159 Дана функция Решение
|
− частное приращение по переменной 
,
− частное приращение по переменной 
.
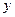к приращениям соответствующих переменных, то они называются частными производными.
, 
от функции 
.
, 
.
.
, 
.
от функции 
.
, 
.
в точке М(3; 4).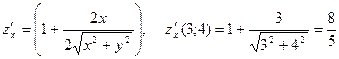
,
.
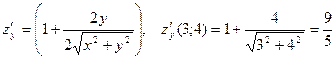. Вычислить 
в точке М0(1; 1; 1).
, 
,
, 
.
