Теплопередача. Основы расчёта теплообменных аппаратовОпределить практическую ширину спектра периодической последовательности прямоугольных импульсов при ширине импульсов
Указание. При решении задачи воспользоваться результатами, полученными при решении задач 1.4, 1.9.
Теплопередача. Основы расчёта теплообменных аппаратов Теоретическая теплотехника как наука состоит из технической термодинамики и теплопередачи. В технической термодинамике объектом изучения является теплота (Дж) и способы её превращения, а в теплопередаче – тепловой поток (Bm = Теплопередача – наука о процессах самопроизвольного распространения теплоты в пространстве с неоднородным полем температур. При теплопередаче происходит обмен тепловой энергией (теплообмен) между теплоносителем и нагреваемой средой. На практике различают три основных вида теплообмена, отличающихся между собой физической сущностью процессов переноса теплоты: теплопроводность, конвективный теплообмен и теплообмен излучением [2]. Теплопроводность – это перенос теплотымежду непосредственно со прикасающимися слоями или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц вещества (молекул, атомов, свободных электронов). В процессе теплообмена теплопроводностью структурные частицы более нагретой части тела при беспорядочном движении сталкиваются с соседними частицами и передают им часть своей кинетической энергии. В результате одна из соприкасающихся частей тела охлаждается, а другая нагревается. Конвективный теплообмен – это такой вид теплообмена, который обусловлен совместным действием двух механизмов переноса теплоты: теплопроводностью и конвекцией, которая осуществляется за счёт движения самой жидкой среды из области высокой температуры в область низкой температуры. Теплообмен излучением – характеризуется переносом энергии от одного тела к другому в виде фатонов или электромагнитных волн. Этот вид теплообмена осуществляется в три этапа: - внутренняя энергия тела преобразуется в энергию излучения; - энергия излучения распространяется в пространстве; - энергия излучения поглощается и преобразуется во внутреннюю энергию нагреваемого тела. Для формирования основных положений теории теплообмена рассмотрим её основные понятия, одним из которых является температурное поле. Температурным полем называется совокупность значений температуры во всех точках тела в данный момент времени. Температурное поле может изменяться во времени и в пространстве. В зависимости от изменения во времени оно может быть стационарным и нестационарным, т.е. не
изменяющимся и изменяющимся. В пространстве температурное поле характеризуется понятием однородности. Если температура в различных точках тела имеет одинаковое значение, то температурное поле называется однородным, а при наличии разности температур оно называется неоднородным. Степень неоднородности температурного поля количественно характеризуется градиентом температуры. Градиент температуры
Отметим, что градиент температуры представляет собой вектор, направленный по нормали к изотермической поверхности в сторону увеличения температуры. Для количественной характеристики интенсивности распространения теплоты в теплопередаче используется понятие вектора плотности теплового потока. Вектор плотности теплового потока ( При практическом использовании понятия плотности теплового потока нет необходимости во всех случаях рассматривать эту величину как вектор. Обычно направление распространения теплоты уже известно и тогда плотность теплового потока можно представить как величину скалярную. Из определения плотности теплового потока следует, что её размерность в системе СИ будет равна В расчётах теплообменных аппаратов часто надо определять не удельный тепловой поток через 1 м2, а полный, проходящий через всю поверхность. В этом случае используют понятие теплового потока (Q), который в случае равенства плотностей теплового потока во всех точках рабочей поверхности, определяется формулой (4.2) Q = qF, Вт, (4.2)
где F – площадь изотермической поверхности, м2 . Так как различные виды теплообмена отличаются физической сущностью проходящих процессов, то и законы, описывающие эти процессы должны быть различны. Передача теплоты теплопроводностью описывается законом Фурье, который устанавливает количественную связь между температурным полем в теле и интенсивностью распространения в нём теплоты. Закон Фурье утверждает, что вектор плотности теплового потока пропорционален вектору градиента температуры:
где Отметим, что знак «минус» в математическом выражении закона Фурье (4.3) обусловлен разнонаправленностью векторов плотности теплового потока и градиента температуры, т.е. теплота распространяется в сторону меньшей температуры, а вектор градиента температуры по определению направлен в сторону большей температуры. Коэффициент теплопроводности является индивидуальной теплофизической характеристикой вещества и изменяется в широких пределах. Его размерность можно определить из уравнения (4.3):
Таким образом, коэффициент теплопроводности численно равен плотности теплового потока при градиенте температуры 1 Несмотря на то, что теплопроводность всегда связана с движением микрочастиц вещества, характер этого движения для газов, жидкостей и твёрдых тел различен. В газахпри обычных давлениях и температурах перенос теплоты осуществляется за счёт перемещения молекул, обладающих определенным запасом кинетической энергии. Вся совокупность молекул газа движется хаотически, молекулы сталкиваются между собой. Для осуществления теплопередачи в заданном объёме газа должны существовать две области с различными температурами. Из молекулярно-кинетической теории следует, что количество молекул переходящих из нагретой области в более холодную, в среднем равно количеству молекул, движущихся в обратном направлении. Но молекулы нагретой области несут с собой большее количество энергии молекулярного движения, чем молекулы холодной области. Тогда результирующий тепловой поток, как разность потоков этих энергий будет представлять собой поток теплопроводности, который направлен из нагретой области в холодную. Значения коэффициентов теплопроводностей различных газов находятся в пределах от 0, 006 до 0, 6 Вт/м·К. Наиболее высокими значениями коэффициентов теплопроводности отличаются гелий и водород, что связано с малой массой молекул этих газов, и их большой подвижностью. Атмосферный воздух при температуре 20оС и давлении 0, 1 МПа имеет В жидкостяхмолекулы расположены почти вплотную друг к другу. Каждая молекула колеблется около положения равновесия, сталкиваясь при этом с соседними молекулами. В процессе взаимодействия центры равновесия молекул могут смещаться, но это смещение происходит с частотой в сотни раз меньшей частоты столкновений молекул. Теплота в жидкости передаётся путём таких сложных и во многом беспорядочных колебаний. Коэффициент теплопроводности различных жидкостей изменяется от 0, 07 до 0, 7 Вт/м·К. Для самой распространенной жидкости в природе - воды коэффициент теплопроводности при 20оС и 0, 1 МПа равен 0, 6 Вт/м·К. ***Сравнить В твёрдых телах механизм распространения теплоты во многом зависит от их структуры. Наиболее значимо это отличие проявляется между металлами и диэлектриками. В металлах носителями теплоты являются свободные электроны, роль которых приблизительно соответствует роли хаотически движущихся молекул газообразного вещества. Поскольку свободные электроны являются одновременно носителями тепловой и электрической энергии то коэффициенты теплопроводности и электропроводности металлов достаточно хорошо коррелируются между собой. Коэффициенты теплопроводности чистых металлов могут достигнуть достаточно больших значений так, например, для меди Диэлектрики, многие из которых имеют пористую структуру, часто используются в качестве теплоизоляционных материалов. В общем случае, пористые материалы состоят из твёрдых зёрен и газа, заполняющего поры. Поэтому они характеризуются некоторой эффективной (условной) теплопроводностью, зависящей от теплопроводности составляющих компонентов. Известно, что коэффициент теплопроводности пористого материала возрастает с увеличением плотности. Например, при возрастании плотности асбеста от 400 до 800
широко используется древесина, которая перед использованием подвергается сушке, что улучшает не только её физико-механические характеристики, но и теплоизоляционные. В промышленных условиях передача теплоты от теплоносителя к нагреваемой среде чаще всего осуществляется через твёрдое тело (металл, строительная конструкция, теплоизолятор и др.), имеющее плоскую или цилиндрическую форму. Плотность теплового потока q для этих тел определяется по расчётным зависимостям, полученным на основе дифференциального уравнения Фурье (4.3) и закона сохранения энергии. Пусть дана плоская стенка из однородного материала с коэффициентом теплопроводности
Постоянную интегрирования С определим исходя из граничных условий (рис.4.1): при x =0 постоянная интегрирования C =
Так как изменение температуры по толщине стенки происходит по закону прямой линии, то при
Для анализа и расчётов уравнение (4.7) более удобно представить как зависимость плотности теплового потока от разности температур, т.е.:
где Отметим, что для определения полного теплового потока Q через площадь стенки F используется уравнение (4.8) в следующем виде:
В этом уравнении:
В теплообменных аппаратах часто в качестве поверхностей разделяющих теплоноситель и нагреваемую среду используются круглые металлические трубы, в которых теплопроводность имеет свои особенности. В отличие от плоских стенок в цилиндрических поверхностях круглых труб температура изменяется по закону логарифма, что находит отражение в уравнении теплопроводности. С учётом изложенного, для цилиндрической стенки уравнение (4.8) трансформируется в уравнение (4.10):
где d1, d2 - диаметры наружной и внутренней поверхностей стенок трубы
Линейная плотность теплового потока представляет собой количество теплоты, которое проходит за единицу времени через цилиндрическую стенку, длина которой равна единице, т.е. В жидкой или газообразной среде перенос теплоты осуществляется не только теплопроводностью, но и конвекцией за счёт движения частиц жидкости или газа, которые сами являются переносчиками теплоты. Т.е. конвективный теплообмен – это такой вид теплообмена, при котором теплота в жидкости или газообразной среде передаётся совместным действием конвекции и теплопроводности. Основные понятия и закономерности передачи тепла теплопроводностью сохраняются и в случае конвективного теплообмена, но становятся более сложными. Так, вектор плотности теплового потока
Здесь: cp – теплоёмкость при постоянном давлении, Дж/кг··К; t - температура жидкости, °С. Конвективная составляющая плотности теплового потока Обычно жидкость при движении соприкасается с поверхностью тела или канала, по которому она протекает. Если при этом температура стенки отличается от температуры жидкости, то происходит конвективный теплообмен между жидкостью и твёрдой стенкой, который называется теплоотдачей. Теплоотдача, как частный случай конвективного теплообмена часто используется в теплотехнической практике. Зависимость плотности теплового потока от разности температур жидкости и поверхности стенки описывается законом Ньютона – Рихмана (4.12):
Из выражения (4.13) следует, что коэффициент теплоотдачи численно равен удельной плотности теплового потока при температурном напоре равном единице. Рассмотренные два вида передачи теплоты (теплопроводность и теплоотдача) являются составляющими более общего процесса теплопередачи, которая осуществляется в теплообменных аппаратах. Теплопередача – это теплообмен между двумя теплоносителями через разделяющую их твёрдую стенку. Процесс теплопередачи комплексный и он может быть разделён на три зоны в зависимости от вида теплообмена (рис. 4.3). Зона I – теплоотдача от горячего теплоносителя и поверхности стенки. Зона II – теплопроводность через твёрдую стенку. Зона III – теплоотдача от поверхности твёрдой стенки к холодному теплоносителю. Согласно закону сохранения энергии при стационарном режиме плотность теплового потока через рассматриваемую плоскую стенку не изменяется. Т.е. к единице левой поверхности стенки (рис. 4.3) в единицу времени от теплоносителя поступает количество теплоты
Разделит каждое из этих уравнений на тепловые коэффициенты
После выполнения простых алгебраических действий будем иметь:
Величину, обратную знаменателю правой части уравнения (4.18) принято обозначать коэффициентом теплопередачи k, т.е.
Тогда уравнение теплопередачи с учётом (4.18) и (4.19) будет иметь следующий вид:
Коэффициент теплоотдачи 1° К. Величина обратная коэффициенту теплопередачи
Как видно из выражения (4.21) полное термическое сопротивление представляет собой сумму термических сопротивлений теплопередачи и термического сопротивления теплопроводности. Уравнение теплопередачи (4.20) с учётом (4.19) лежит в основе расчётов теплообменных аппаратов. Конвективный теплообмен позволяет обеспечить сравнительно малые потоки, когда температура теплоносителя не превышает 300÷ 400°С. Для создания мощных тепловых потоков обычно используют теплообмен излучением. Газ, образующийся при горении топлива, имеет температуру более 1000°С и передаёт в окружающую среду большую часть своей энергии в виде излучения. Другим примером эффективного применения теплового излучения является микроволновые печи, которые в настоящее время широко используются для термообработки пищевых продуктов. Теплообмен излучением представляет собой такой вид теплообмена, при котором энергия передаётся электромагнитными волнами (фатонами). Природа световых волн идентична природе электромагнитных, т.е. лучистая энергия представляет собой электромагнитные волны, скорость распространения которых равна 300 тысяч километров в секунду. В этом случае теплота передаётся на расстоянии при отсутствии непосредственного контакта тел, обменивающихся теплотой, что значительно упрощает конструкции теплообменных аппаратов. В общем случае лучистый поток Qo, падающий на тело распадается на три составляющих потока:
Энергия потока поглощённого телом
Для двухатомных газов, которые не отражают лучей Тело, поглощающее всю падающую на него энергию, называется абсолютно чёрным. С учётом (4.23) для абсолютно чёрного тела коэффициент поглощения Основной характеристикой излучающего тела является его излучающая способность, которая зависит от температуры поверхности тела. В расчётах лучистых потоков используется понятие поверхностной плотности
где σ о – постоянная Стефана-Больцмана (σ о = 5, 67· 10-8
Реальные «серые» тела обладают несколько меньшей излучательной способностью, для характеристики которой используется коэффициент черноты
где спр–приведённый коэффициент излучения, S –площадь плоской поверхности, м2. Проведённый коэффициент излучения является комплексной характеристикой и определяется по формуле (4.26):
где:
Отметим, что в уравнении (4.26) вместо коэффициентов В таблице 4.1 приведены значения коэффициентов излучения некоторых часто встречающихся материалов.
Таблица 4.1
Наряду с созданием мощных потоков на практике часто решается задача защиты от теплового излучения. В качестве защиты рекомендуется исполь- зовать твёрдые тонкие экраны, изготовленные из материала с большой отражательной способностью.
|

 для случая, когда должны быть учтены все гармонические составляющие сигнала, содержащие не менее 95% общей мощности сигнала.
для случая, когда должны быть учтены все гармонические составляющие сигнала, содержащие не менее 95% общей мощности сигнала. ).
).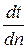 равен пределу отношения изменения температуры
равен пределу отношения изменения температуры  вдоль нормали изотермической поверхности к соответствующему её отрезку
вдоль нормали изотермической поверхности к соответствующему её отрезку 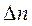 , если длина этого отрезка стремиться к нулю (4.1)
, если длина этого отрезка стремиться к нулю (4.1)
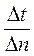
 (4.1)
(4.1)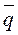 , Вт/м2) направлен по нормали к изотермической поверхности в сторону уменьшения температуры, а его длина численно равна количеству теплоты, которое проходит через единицу площади изотермической поверхности в единицу времени.
, Вт/м2) направлен по нормали к изотермической поверхности в сторону уменьшения температуры, а его длина численно равна количеству теплоты, которое проходит через единицу площади изотермической поверхности в единицу времени.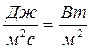 .
. = -
= -  , (4.3)
, (4.3) - коэффициент теплопроводности.
- коэффициент теплопроводности. (4.4)
(4.4) .
.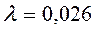 Вт/м·К.
Вт/м·К.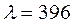 Вт/м·К.
Вт/м·К. его коэффициент теплопроводности увеличивается от 0, 1 до 0, 25 Вт/м·К. Эффективная теплопроводность пористых материалов в большей степени зависит от их влажности, т.е. с увеличением влажности
его коэффициент теплопроводности увеличивается от 0, 1 до 0, 25 Вт/м·К. Эффективная теплопроводность пористых материалов в большей степени зависит от их влажности, т.е. с увеличением влажности  возрастает. В Сибирских регионах в качестве конструкционного материала
возрастает. В Сибирских регионах в качестве конструкционного материала , который не зависит от температуры. Толщина этой стенки намного меньше ширины и высоты, что позволяет считать стенку тонкой, а задачу одномерной. Левая поверхность стенки, представляет собой изотермическую плоскость и имеет температуру
, который не зависит от температуры. Толщина этой стенки намного меньше ширины и высоты, что позволяет считать стенку тонкой, а задачу одномерной. Левая поверхность стенки, представляет собой изотермическую плоскость и имеет температуру  , а правая температуру
, а правая температуру 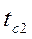 , причём
, причём 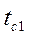 >
> 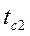 (рис. 4.1). Для вывода уравнения зависимости плотнос-
(рис. 4.1). Для вывода уравнения зависимости плотнос-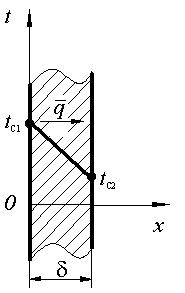 Рис. 4.1.
Рис. 4.1.
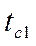 и
и 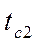 необходимо проинтегрировать дифференциальное уравнение закона Фурье (4.3). Если это уравнение представить в виде
необходимо проинтегрировать дифференциальное уравнение закона Фурье (4.3). Если это уравнение представить в виде 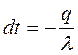 dx и произвести интегрирование, то получим выражение (4.5):
dx и произвести интегрирование, то получим выражение (4.5):
 , (4.5) где x – координата точки поверхности стенки;
С – постоянная интегрирования.
, (4.5) где x – координата точки поверхности стенки;
С – постоянная интегрирования.
 . Тогда уравнение (4.5) запишется в виде (4.6):
. Тогда уравнение (4.5) запишется в виде (4.6): (4.6)
(4.6)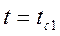 и
и 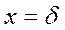 из уравнения (4.6) получим:
из уравнения (4.6) получим: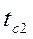 =
= 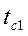 -
-  (4.7)
(4.7)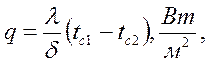 (4.8)
(4.8) - толщина стенки, м.
- толщина стенки, м.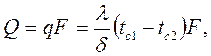 Вт (4.9)
Вт (4.9)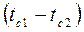 - температурный напор;
- температурный напор; - термическая проводимость.
- термическая проводимость.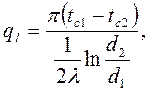 (4.10)
(4.10) - линейная плотность теплового потока.
- линейная плотность теплового потока. r.
r. при конвективном теплообмене определяется не только градиентом температуры в жидкости, но и полем скорости (4.11):
при конвективном теплообмене определяется не только градиентом температуры в жидкости, но и полем скорости (4.11):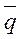 =
= 
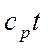 , (4.11)
, (4.11)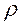 - плотность жидкости, кг/м3;
- плотность жидкости, кг/м3;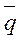 непосредственно связана с полем скорости движения жидкости и представляет собой количество теплоты, которое переносится в направлении вектора скорости
непосредственно связана с полем скорости движения жидкости и представляет собой количество теплоты, которое переносится в направлении вектора скорости  через единицу поверхности. Носителем теплоты в этом процессе является жидкость с массовым расходом через единицу поверхности равным
через единицу поверхности. Носителем теплоты в этом процессе является жидкость с массовым расходом через единицу поверхности равным 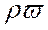 , кг/м2с.
, кг/м2с.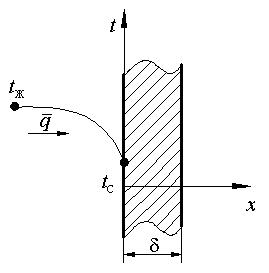 Рис. 4.2
Рис. 4.2
 , (4.12)
где tc -температура поверхности
стенки, °С;
, (4.12)
где tc -температура поверхности
стенки, °С;
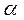 -коэффициент теплоотдачи,
-коэффициент теплоотдачи,  (tc – tж) – температурный напор.
Коэффициент теплоотдачи
(tc – tж) – температурный напор.
Коэффициент теплоотдачи  , исходя из уравнения (4.12), можно пред- ставить в виде:
, исходя из уравнения (4.12), можно пред- ставить в виде: 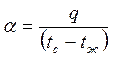 (4.13)
(4.13)
 . Это же количество теплоты
. Это же количество теплоты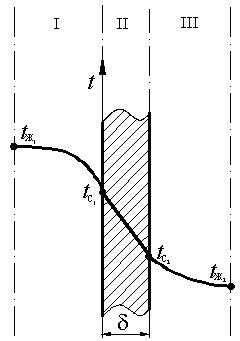 Рис. 4.3
Рис. 4.3
 (4.14)
(4.14)  (4.15)
(4.15)
 (4.16)
(4.16)
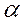 ,
,  ,
, 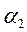 и, сложив их, получим общее уравнение (4.17):
и, сложив их, получим общее уравнение (4.17): 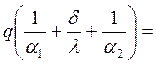
 (4.17)
(4.17) (4.18)
(4.18) ,
,  (4.19)
(4.19)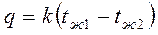 ,
,  (4.20)
(4.20)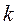 характеризует интенсивность теплопередачи и численно равен плотности теплового потока при разности температур
характеризует интенсивность теплопередачи и численно равен плотности теплового потока при разности температур , называется полным термическим сопротивлением:
, называется полным термическим сопротивлением: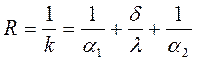 , (4.21)
, (4.21) - поглощённый телом;
- поглощённый телом; - отражённый телом;
- отражённый телом; - прошедший через тело, т.е.:
- прошедший через тело, т.е.: (4.22)
(4.22) трансформируется в тепловую энергию нагреваемого тела. Её доля характеризуется коэффициентом поглощения
трансформируется в тепловую энергию нагреваемого тела. Её доля характеризуется коэффициентом поглощения  . Доля энергии отражённого потока определяется коэффициентом отражения
. Доля энергии отражённого потока определяется коэффициентом отражения 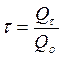 . Тогда по определению сумма этих трёх коэффициентов будет равна единице:
. Тогда по определению сумма этих трёх коэффициентов будет равна единице: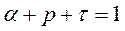 (4.23)
(4.23) 0, тогда уравнение (4.23) примет более простой вид:
0, тогда уравнение (4.23) примет более простой вид:  .
.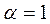 . Абсолютно чёрное тело – это идеальная модель, а реальные тела к этой модели в какой-то степени могут приближаться. Например, близки по своим свойствам к чёрному телу бархат и сажа. Известно, что чем больше шероховатость тела, тем выше значение его коэффициента поглощения.
. Абсолютно чёрное тело – это идеальная модель, а реальные тела к этой модели в какой-то степени могут приближаться. Например, близки по своим свойствам к чёрному телу бархат и сажа. Известно, что чем больше шероховатость тела, тем выше значение его коэффициента поглощения. , которое понимается как отношение потока излучения к площади поверхности испускания и имеет размерность
, которое понимается как отношение потока излучения к площади поверхности испускания и имеет размерность 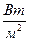 . Зависимость между тепловым излучением абсолютно чёрного тела и абсолютной температурой определяется законом Стефана-Больцмана:
. Зависимость между тепловым излучением абсолютно чёрного тела и абсолютной температурой определяется законом Стефана-Больцмана: σ оT4, (4.24)
σ оT4, (4.24) );
); - поверхностная плотность потока абсолютно чёрного тела.
- поверхностная плотность потока абсолютно чёрного тела. . Значение
. Значение  определяется как отношение коэффициента излучения серого с и абсолютно чёрного тела со, т.е.
определяется как отношение коэффициента излучения серого с и абсолютно чёрного тела со, т.е.  =
=  . Тогда теплообмен излучением между плоскими параллельными поверхностями двух серых тел с температурами Т1 и Т2 по закону Стефана-Больцмана выражается следующим уравнением:
. Тогда теплообмен излучением между плоскими параллельными поверхностями двух серых тел с температурами Т1 и Т2 по закону Стефана-Больцмана выражается следующим уравнением: , (4.25)
, (4.25)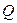 - поток лучистой энергии, Вт;
- поток лучистой энергии, Вт; ,
,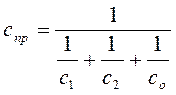 , (4.26)
, (4.26)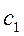 и
и 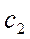 - коэффициенты излучения тел, обменивающихся теплотой, (
- коэффициенты излучения тел, обменивающихся теплотой, ( );
); - коэффициент излучения абсолютного чёрного тела (
- коэффициент излучения абсолютного чёрного тела ( = 5, 57
= 5, 57  )
) и
и  могут быть использованы степени черноты этих тел:
могут быть использованы степени черноты этих тел:  и
и  .
.


