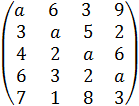ЭКОНОМИЧЕСКОЕ МОДЕЛИРОВАНИЕ МЕТОДАМИ ТЕОРИИ ИГРЦель: ознакомиться с методами решения экономических задачв условиях конфликтных ситуаций используя математическую модельтеории матричных игр на ЭВМ. Рассмотрим методы принятия управленческих решений в условиях конфликта, когда в ситуации участвуют две стороны, интересы которых противоположны. Это могут быть, например, отношения продавца и покупателя, банка и заемщика, истца и ответчика. Для решения таких задач используют методы теории игр, для анализа которых удобно использовать ЭВМ. Пусть в игре участвуют два игрока А и В. Игрок А имеет n чистых стратегий, а игрок В – m стратегий. А выигрывает у В сумму a ij, если А выбрал вариант i (i=1, 2, …, n), а В выбрал вариант j (j=1, 2, …, m).Тогдаплатежнаяматрицаигрыимеетвид:
A = [ a ij ] = a 21 a 22 … a 2m ……….. a n1 a n2… a nm
Для нахождения вероятностей pi и qj оптимальных смешанных стратегий необходимо решать прямую и двойственную задачи линейного программирования (ЗЛП) вида: а) прямая ЗЛП – минимизировать Z = x 1+ x 2+…+ x n при ограничениях
a 12 x 1+ a 22 x 2+…+ a n2 x n≥ 1, (5.1) ……………………. …… a 1m x 1+ a 2m x 2+…+ a nm x n≥ 1, x 1, x 2, …, x n≥ 0. Обращаем внимание: строка ограничения формируется из столбца платежной матрицы! Решая ее, находим оптимальное решение x 1*, x 2*, …, x n*, откуда, разделив на Z*= x 1*+ x 2*+…+ x n*, получаем оптимальную стратегию для игрока А (р 1*, р 2*,.., рn *), которая заключается в применении i-й чистой стратегии с частотой рi *= хi */ Z*. б) двойственная ЗЛП – максимизировать F = y 1+ y 2+ … + y m→ max;
a 11 y 1+ a 12 y 2+ …+ a 1m y m≤ 1; a 21 y 1+ a 22 y 2+ …+ a 2m y m ≤ 1; (5.2) ………………………….. a n1 y 1+ a n2 y 2+ …+ an m y m≤ 1; y 1≥ 0; y 2≥ 0; …y m≥ 0. Здесь строка ограничения формируется из строки платежной матрицы. Решая данную ЗЛП, находим оптимальное решение у 1*, у 2*, …, у m*, откуда, разделив на F *= y 1*+ y 2*+…+ y m*, получаем оптимальную стратегию для игрока B (q 1*, q 2*,.., qm *), которая заключается в применении j-й чистой стратегии с частотой qj *= yj */ F *. Затем находим цену игры g =1/ Z* =1 /F*. ПРИМЕР 5.1. Две конкурирующие коммерческие организации А и В выпускают продукцию одного вида. Каждая организация планирует проведение рекламной акции, причем маркетологи каждой компании предложили четыре сценария ее проведения A 1, A 2, A 3, A 4– для компании А и B 1, B 2, B 3, B 4– для компании В. Ожидаемая прибыль для кампании А при каждой ее стратегии Ai и ответе Bj представлена в платежной матрице:
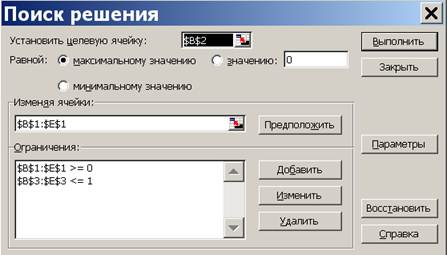
Необходимо найти оптимальные стратегии для обоих игроков А и В в предположении, что чем больше выигрыш одного игрока, тем он меньше для другого. Определить среднюю прибыль А. Рассмотрим задачу со стороны игрока А. Для ее решения нужно составить соответствующую задачу линейного программирования, тоесть необходимо найти минимум функции x 1 + x 2 + x 3 + x 4 → min; при ограничениях: 70 x 1 + 60 x 2 + 20 x 3 +50 x 4≥ 1; 30 x 1 + 50 x 2 + 60 x 3 + 70 x 4 ≥ 1; 20 x 1 + 40 x 2 + 80 x 3 + 30 x 4 ≥ 1; 50 x 1 +80 x 2 + 60 x 3 + 50 x 4 ≥ 1; x 1 ≥ 0; x 2 ≥ 0; x 3 ≥ 0; x 4 ≥ 0. Для решения данной ЗЛП на ЭВМ также используют надстройку EXCEL «Поиск решения». Подготовим предварительно в электронной таблице данные. Запускаем программу MS Excel, вводим в ячейку А1 открывшейсяэлектронной таблицы подпись «Переменные», а в следующие ячейкиВ1-Е1произвольные значения переменных x 1, x 2, x 3, x 4. Это вначале могут быть произвольные числа, например единицы. Далее, в ячейку А2 вводим подпись «Целевая», а в соседнюю ячейку В2 значение целевой функции (переключившись в английский режим набора текста): «=B1+С1+D1+Е1»или =SUMM(B1: E1), что означает формулу x 1 + x 2 + x 3 + x 4. В третьей строке вводятся левые части системы ограничений. Для этого переводим курсор в ячейку А3 и вводим в ней текст «Ограничения», а в ячейку В3 формулу «=70*В1+60*C1+20*D1+50*E1», которая соответствует левой части первого ограничения системы. Три остальных ограничения вводим в ячейки С3-В3, а именно, в ячейку С3: «=30*В1+50*C1+60*D1+70*E1», в D3: «=20*В1+40*C1+80*D1+30*E1», в ячейку Е3: «=50*В1+80*C1+60*D1+50*E1». После этого вызываем надстройкуСервис/Поиск решения, в поле «Установить целевую ячейку» даем ссылку на В2. Ниже, в области «Равной», поставить переключатель на минимальное значение. Ставим курсор в поле «Изменяя ячейки», и даем ссылки на переменные, обводя мышью ячейки В1-Е1. Далее, переводим курсор в поле «Ограничения», и вводим ограничения. Для этого нажимаем на кнопку «Добавить» и в появившемся окне в поле «Ссылка наячейку» даем ссылку на ячейки, содержащие левые частивсех четырех ограничений, которые хранятся в ячейках В3: Е3 (то есть переводим курсор в поле «Ссылка на ячейку» и обводим мышью ячейки В3: Е3). В центральном поле выбираем знак неравенства – ограничения: «≥», в поле «Ограничение» вводим единицу. Нажимаем «ОК». Для ввода дополнительных ограничений x 1≥ 0; x 2≥ 0; x 3≥ 0; x 4≥ 0нажимаем «Добавить», в поле «Ссылка на ячейку» ставимкурсор и обводим ячейки В1-Е1, выводим в центральное поле «≥», ограничение «0», нажимаем «ОК». Результат на рис.5.1.
Рисунок 5.1 Окно«Поиск решения» прямой ЗЛП Для запуска вычислений нажимаем кнопку «Выполнить». Появляется надпись, что решение найдено. Выбираем «Сохранить найденное решение» и нажимаем «ОК» – видим результат (рис.5.2): x 1=0, x 2 =0, 015, x 3 =0, 05, x 4 =0, что видно из ячеек В1-Е1.
Рисунок 5.2 Решение прямой ЗЛП примера 5.1 Вводим в А5 подпись «Цена игры», а в соседнюю В5 формулу (переключаясь на английский язык) «=1/(В1+С1+D1+Е1)» или =1/В2. Результат: 50. Это средняя вероятность выигрыша для игрока А. Находим вероятности чистых стратегий в смешанной стратегии р. Для этого вводим в А6 подпись «Р1=», а в соседнюю В6 формулу «=В5*В1», вводим в А7: «Р2=», а в В7 формулу «=В5*С1», в А8: «Р3=», а в В8: «=В5*D1», в А9: «Р4=», в В9: «=В5*Е1». Данные показатели и есть решение задачи(рис.5.3).
Рисунок 5.3 Решение примера 5.1 для игрока А Рассмотрим теперь решение относительно игрока В. ЗЛП для игрока В имеет вид: y 1+ y 2+ y 3+ y 4→ max; 70 y 1+30 y 2+ 20 y 3+ 50 y 4≤ 1; 60 y 1+ 50 y 2+ 40 y 3+ 80 y 4≤ 1; 20 y 1+ 60 y 2+ 80 y 3+ 60 y 4≤ 1; 50 y 1+ 70 y 2+ 30 y 3+50 y 4≤ 1; y 1≥ 0; y 2≥ 0; y 3≥ 0; y 4≥ 0. Переходим на «Лист2» электронной таблицы, щелкнув на соответствующей закладке внизу таблицы. Вводим в ячейки открывшейся чистой электронной таблицы в ячейку А1 надпись «Переменные», а в следующие ячейкиВ1-Е1 произвольные значения переменных, например, цифры 1. В ячейку А2 вводим подпись «Целевая». Вводим в ячейку В2 значение целевой функции (переключившись в английский режим набора текста): «=B1+С1+D1+Е1», что означает формулу y 1+ y 2+ y 3+ y 4. В третьей строке вводятся левые части системы ограничений. Для этого переводим курсор в ячейку А3 и вводим в ней текст «Ограничения». Переключившись в английский режим клавиатуры, вводим в ячейку В3 формулу «=70*В1+30*C1+20*D1+50*E1», которая соответствует левой части первого ограничения системы. Вводим в ячейку С3: «=60*В1+50*C1+40*D1+80*E1», в D3: «=20*В1+60*C1+80*D1+60*E1», в ячейку Е3: «=50*В1+70*C1+30*D1+50*E1». После этого вызываем вменю «Cервис» надстройку «Поиск решений». В поле «Установить целевую ячейку» даем ссылку на В2. Ниже, в области «Равной», поставить переключатель на максимальное значение. Ставим курсор в поле «Изменяя ячейки», и даемссылки на переменные, обводя мышью ячейки В1-Е1. Далее, переводим курсор в поле «Ограничения», и вводимограничения. Для этого, нажимаем на кнопку «Добавить» и далее в поле «Ссылка на ячейку» обводим ячейкиВ3: Е3, содержащие левые частивсех четырех ограничений, в центральном поле выбираем знак неравенства – ограничения: «≤», в поле «Ограничение» вводим единицу. Нажимаем «ОК». Для ввода дополнительных ограничений y 1≥ 0; y 2≥ 0; y 3≥ 0; y 4≥ 0 нажимаем «Добавить», в поле «Ссылка на ячейку» ставим курсор и обводим ячейки В1-Е1, выводим в центральное поле «≥», ограничение «0», нажимаем «ОК». Результат на рис.5.4.
Рисунок 5.4 Окно«Поиск решения»обратной ЗЛП Далее запускаем программу, нажимая «Выполнить».Результат решения обратнойЗЛП в ячейках В1-Е1. Вводим в А5 подпись «Ценаигры», а в соседнюю В5 формулу (переключаясь на английский язык)«=1/(В1+С1+D1+Е1)». Находим вероятности чистых стратегий q всмешанной стратегии игрока В. Для этого вводим в А6 подпись «q1=», а в соседнюю В6 формулу «=В5*В1», вводим в А7: «q2=», а в В7 формулу «=В5*С1», в А8: «q3=», а в В8: «=В5*D1», в А9: «q4=», вВ9: «=В5*Е1». Данные показатели и есть решение задачи для игрока В(рис.5.5).
Рисунок 5.5 Решение примера 5.1 для игрока В ПРИМЕР 5.2. Построить прямую и двойственную задачи линейного программирования для решения матричной игры, заданной платежной матрицей: A= Прямая и двойственная задачи линейного программирования имеют вид: x 1 + x 2 + x 3 + x 4 + x 5 → min; a x 1 + 3 x 2 + 4 x 3 + 6 x 4 + 7 x 5 ≥ 1; 6 x 1 + a x 2 + 2 x 3 + 3 x 4 + x 5 ≥ 1; 3 x 1 +5 x 2 + a x 3 +2 x 4 +8 x 5 ≥ 1; 9 x 1 +2 x 2 +6 x 3 + a x 4 +3 x 5 ≥ 1; x i ≥ 0; i=1, 2, 3, 4, 5.
y 1 + y 2 + y 3 + y 4 → max; a y 1 + 6 y 2 + 3 y 3 + 9 y 4 ≤ 1; 3 y 1 + a y 2 + 5 y 3 + 2 y 4 ≤ 1; 4 y 1 + 2 y 2 + a y 3 +6 y 4 ≤ 1; 6 y 1 + 3 y 2 + 2 y 3 + a y 4 ≤ 1; 7 y 1 + y 2 + 8 y 3 + 3 y 4 ≤ 1; yj ≥ 0; j=1, 2, 3, 4. Из решения игры можно найти цену игры g =1/(x 1 + x 2 + x 3 + x 4 + x 5) =1/(y 1 + y 2 + y 3 + y 4) и вероятности состояний pi = xi g, (i = 1, 2, 3, 4, 5); qj = yj g, (j =1, 2, 3, 4). Задание 5.1. Самостоятельно с использованием ЭВМ решить поставленные в примере 5.2 ЗЛП и найти оптимальные смешанные стратегии дляигроков А и В. Значение неизвестного параметра а взять равным номеру варианта. Отчет должен содержать решения поставленных ЗЛП (значения переменных xiu yj, значения целевых функций), смешанные стратегии для обоих игроков и цену игры g. Задание 5.2. Директор предприятия А заключает договор сконкурирующей фирмой В о реализации своей продукции на конкретной территории областного центра. Конкурирующие стороны выделили пять районов области. Каждая из них может развивать свое производство в этих пяти районах: A 1, A 2, A 3, A 4, A 5– длястороны А и B 1, B 2, B 3, B 4, B 5– для В. Вероятности успеха для стороны А приведены в платежной матрице:
Определить оптимальные стратегии для каждой стороны. Значение неизвестного параметра а взять равным номеру варианта. Отчет должен содержать математические модели ЗЛП, составленные для игроков Аи В, их решения, оптимальные смешанныестратегии для игроков А и В, цену игры g, выводы, в каких районах предприятие А должно реализовывать свою продукцию и в каких пропорциях, чтобы получить оптимальную прибыль вне зависимости от поведения конкурента В и чему равна эта прибыль. Задание 5.3. Решить игру, описанную платежной матрицей для обоих игроков (матрица приведена для игрока А).
Значение неизвестного параметра а взять равным номеру варианта. Отчет должен содержать математические модели ЗЛП, составленные для обоих игроков, полученные в результате решения на ЭВМ смешанные стратегии для обоих игроков и цену игры g.
|
a 11 a 12 … a 1m
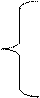a 11 x 1+ a 21 x 2+…+ a n1 x n≥ 1,
при ограничениях
