Система уравнений движения вязкого сжимаемого теплопроводного газа. Простейшие физические процессыСистема уравнений, описывающая движение газа или жидкости, основывается на законах сохранения (массы, импульса, энергии и т.д.). 1. Закон сохранения масс или уравнение неразрывности.
получаем закон сохранения масс в дифференциальной форме (см.[14]):
2. Закон сохранения импульса. Уравнения движения Из второго закона Ньютона где Пусть вектор
Плотность массовых сил можно определить по формуле
Окончательно, в дифференциальном виде, в векторной форме записи уравнения движения получаются следующие (см.[14]):
Здесь 3. Уравнение энергии. Закон сохранения энергии Закон сохранения энергии, заключенной в объеме V, может быть записан(см.[5]):
Слева написано изменение количества полной энергии, заключенной в объеме V. Первый член справа – полная энергия, непосредственно переносимая (в единицу времени) проходящей через поверхность S массовой жидкости. Второй член представляет работу, производимую силами давления над жидкостью, заключенной внутри поверхности S. Последующие слагаемые учитывают энергию, связанную с тепловым потоком, вектором внешних сил и мощностью тепловых источников. Преобразуя уравнение, получим его дифференциальную форму:
Здесь Вектор плотности теплового потока вычисляется по закону Фурье Система дифференциальных законов сохранения (1) – (3) неполная, необходимо присоединить замыкающие соотношения. Это уравнения состояния и потоковые соотношения. Потоковые соотношения выражают гидродинамические потоки импульса и энергии через градиенты вектора состояния течения. Термодинамическое равновесие среды описывается пятью функциями:
В случае совершенного газа используется уравнение состояния Клапейрона–Менделеева: В предположении ньютоновской среды справедливо уравнение, связывающее тензор напряжений Р и тензор скоростей деформации Ф.
Здесь Заметим, что в любой системе координат будет выполняться равенство: Используя физическое представление системы уравнений (1) – (7) (системы уравнений Навье – Стокса), запишем ее в векторной дивергентной форме, удобной для математических преобразований (см.[6]):
где Будем называть вектор
Выделим базисные физические процессы и проведем их анализ для уравнений (8). Переходя к полной индексной записи системы уравнений (8): Выделим три физических процесса для первого вектора гидродинамического потока (см.[6]):
здесь G={ В общем случае матрица w1=
матрица w3
Рассмотрим первый физический процесс. Выпишем систему уравнений, в которой мы пренебрегаем силами, связанными с давлением и диссипативными эффектами:
Эта система описывает слабомолекулярное течение жидкости или газа и имеет гиперболический характер. Исследуем первые четыре уравнения системы (уравнение неразрывности и три уравнения движения). Начнем с уравнений движения:
Из первого уравнения системы (уравнения неразрывности) следует:
Из уравнения (9) вычтем уравнение (10), тогда:
Таким образом, скорость каждого элемента сохраняется вдоль траектории. Для второго физического процесса, если в исходной системе (8) пренебречь силами, связанными с инерцией и диссипацией, а рассмотреть только действие сил, связанных с давлением, получаем следующую систему:
Здесь Видно, что плотность не зависит от времени, поэтому ее можно вынести за знак производной во втором и третьем уравнениях. Учитывая суммирование по повторяющимся индексам, получаем систему:
В уравнениях движения выражаем производные по времени через производные по пространству, тогда
Подставляя частную производную
Теперь воспользуемся уравнением состояния
Подставляем последнее уравнение в предыдущее и получаем:
Из последнего уравнения выразим частные производные скорости по пространственным координатам через производную давления по времени:
Дифференциальным следствием этого уравнения будет уравнение
Опять используем уравнения движения: - Если пренебречь инерционными силами и давлением (третий физический процесс), то получим систему:
Здесь суммирование и по индексу β. В этом случае, как и в двух предыдущих, считаем, что В отсутствии давления тензор вязких напряжений равен:
Системa параболического типа. Рассмотрены три простейшие базисные физические модели. Каждая из них выделяет простой физический процесс. Для получения более сложных моделей будем рассматривать комбинации простейших процессов.
|


 . (1)
. (1) ,
,
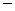 поверхностные и
поверхностные и 
 определяет плотность поверхностных сил. Поверхностные силы, действующие на конечный объем, равны
определяет плотность поверхностных сил. Поверхностные силы, действующие на конечный объем, равны .
.
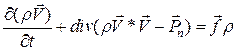 . (2)
. (2)

 . (3)
. (3)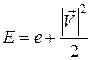 – массовая плотность полной энергии,
– массовая плотность полной энергии,  – вектор плотности теплового потока,
– вектор плотности теплового потока, 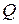 – мощность тепловых источников и F= f ρ – вектор внешних сил.
– мощность тепловых источников и F= f ρ – вектор внешних сил.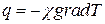 , где
, где  – коэффициент теплопроводности.
– коэффициент теплопроводности. , две из которых независимые, для нахождения остальных используются следующие уравнения состояний
, две из которых независимые, для нахождения остальных используются следующие уравнения состояний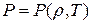 ,
,  ,
,  , (4)
, (4) ,
,  ,
,  , (5)
, (5) ,
,  ,
,  . (6)
. (6) .
. . (7)
. (7)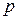 – статистическое давление,
– статистическое давление,  – коэффициенты динамической и объемной вязкости,
– коэффициенты динамической и объемной вязкости,  – единичный тензор и
– единичный тензор и 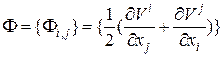 – тензор скоростей.
– тензор скоростей. .
. , (8)
, (8) (идет суммирование по повторяющемуся индексу).
(идет суммирование по повторяющемуся индексу).
 ;
; 

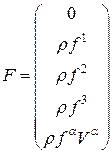
 заметим, что матрица гидродинамических потоков
заметим, что матрица гидродинамических потоков  может быть представлена как сумма трех матриц:
может быть представлена как сумма трех матриц: 
 ,
, }
} 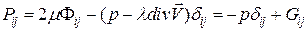 .
. , матрица w2
, матрица w2  и
и .
. .
.

 . (9)
. (9) и после умножения на
и после умножения на  получаем
получаем . (10)
. (10)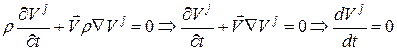 .
. ,
, - символы Кронекера.
- символы Кронекера.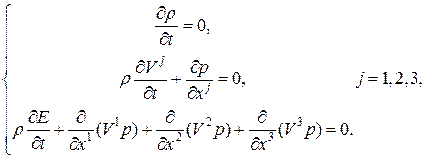
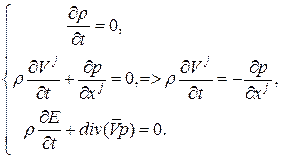
 в последнее уравнение системы, преобразуем его к виду
в последнее уравнение системы, преобразуем его к виду . Для дальнейшего преобразования используем уравнения движения. Умножаем равенства
. Для дальнейшего преобразования используем уравнения движения. Умножаем равенства на координаты
на координаты  и дальше суммируя в последней записи правые и левые части уравнений по индексу j, приходим к векторному равенству:
и дальше суммируя в последней записи правые и левые части уравнений по индексу j, приходим к векторному равенству: 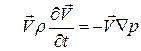 . Окончательно уравнение энергии приводится к виду
. Окончательно уравнение энергии приводится к виду  .
. и найдем частную производную
и найдем частную производную

 .
.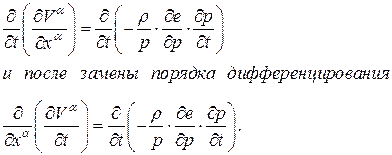
 , которые подставляем в дифференциальное следствие, получаем
, которые подставляем в дифференциальное следствие, получаем . Рассмотрим последнее равенство. Так как
. Рассмотрим последнее равенство. Так как 
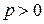 и
и  то полученное уравнение для давления является уравнением гиперболического типа. То есть в этом случае система также носит гиперболический характер.
то полученное уравнение для давления является уравнением гиперболического типа. То есть в этом случае система также носит гиперболический характер.
 .
.
 Подставляя его в уравнения и преобразуя их, получаем:
Подставляя его в уравнения и преобразуя их, получаем:



