Понятие о монотонных разностных схемахСвойство монотонности характеризует качество схемы, ее пригодность для расчета решений с большими градиентами. Разностные схемы при симметричных аппроксимациях не обладают, как правило, свойством монотонности. Свойством монотонности обладают схемы первого порядка аппроксимации. Для схем более высокого порядка удовлетворение этого требования приводит к ухудшению других свойств. При расчете разрывных течений происходят осцилляции численного решения на разрывах и надо проводить процедуру сглаживания решения, что требует введения дополнительных членов в схему. Поэтому предпочтительно использование монотонных схем. Рассмотрим (см.[7]) один из подходов построения монотонных схем предложенный в работах Уорминга и Стэгера. В силу гиперболичности системы уравнений газовой динамики матрица Матрица
= Используя теперь свойство однородности системы уравнений газовой динамики преобразуем вектор
Таким образом вектор потока представлен в виде неотрицательного вектора Рассмотрим как используется такое представление вектора потока для построения монотонных схем на примере явной схемы Маккормака. Явная схема Маккормака второго порядка аппроксимации с учетом (34) в этом случае будет следующая:
В схеме используются обозначения для конечных разностей:
2.7. Схемы для одномерных уравнений газовой динамики и Навье – Стокса представленные в недивергентной форме При решении систем уравнений газовой динамики и Навье – Стокса могут использоваться несколько форм представления уравнений: дивергентная, недивергентная и предельно дивергентная. Ранее были рассмотрены различные виды разностных схем для системы уравнений записанных в дивергентной форме. В результате линеаризации уравнений получаются сложные матрицы Якоби В и С, которые вносят дополнительные трудности в численные расчеты. Выбор искомого вектора состояния в газодинамических переменных в одной из эквивалентных форм позволяет строить разностные схемы наиболее просто и экономично реализующие. Как правило, для уравнений газовой динамики вектор состояния Уравнения газовой динамики, представленные в переменных
Здесь матрица Для уравнений Навье-Стокса краевые условия задаются для скорости и температуры, поэтому и схемы в этих переменных используются наиболее часто. Рассмотрим систему уравнений Навье – Стокса в переменных
Здесь матрица
Матрица Разностные схемы для модельных уравнений могут быть использованы и для систем уравнений газовой динамики и Навье – Стокса, так схема с весами в этом случае равна:
Схема (37) аппроксимирует системы уравнений (35) и (36) с порядком Для уравнений газовой динамики
а для уравнений Навье- Стокса
При несимметричной аппроксимации производных Из вида матриц Схема (37) в линейном приближении безусловно устойчива при Выведем условие устойчивости для схемы (37) в случае решения системы уравнений газовой динамики (35) при симметричной аппроксимации пространственных переменных. Для исследования устойчивости схемы с весами
подставляем гармонику
После его упрощения и замены
Обозначим
Найдем корни уравнения.
Возвращаясь к исходным обозначениям получаем для первого корня:
Для двух других корней:
Схема безусловно устойчива при Для получения схем, реализующихся скалярными прогонками, необходимо ряд слагаемых, например слагаемые с Другой подход получения экономичных схем основан на применении метода расщепления по физическим процессам. В качестве модельной задачи, выберем систему уравнений газовой динамики в переменных
Система (38) недивергентного вида и давление исключено из этой системы с помощью уравнения состояния:
Воспользуемся расщепление дифференциального оператора по физическим процессам:
Оператор Систему уравнений (38) с учетом расщепления дифференциального оператора заменим сиcтемой:
слабо аппроксимирующей исходную систему (см.[6]). Полученную систему уравнений аппроксимируем следующей разностной схемой с весами:
Переписывая уравнения схемы (39) в каноническом виде:
и умножая первое уравнение слева на оператор
Операторы Для системы (38) разностная схема (39) имеет первый порядок аппроксимации по времени и k-тый по пространству. Реализация схемы на дробных шагах Рассмотрим численную реализацию системы (39). На первом дробном шаге вид оператора 1) Если выбрать
Если Когда знак скорости меняется в расчетной области, то решение находится скалярной трехточечной прогонкой. В этом случае разностное уравнение имеет вид:
где Прогонка хорошо обусловлена при аппроксимации с порядком 2) Если выбрать На втором дробном шаге схемы (39) решается следующая система уравнений:
В уравнении движения для аппроксимации используется сопряженный разностный оператор. Исключая Исследуем устойчивость схемы (39) для линеаризованных уравнений, полученных из системы (38) методом замороженных коэффициентов. Решение разностных уравнений будем искать в виде Для первого дробного шага получаем характеристическое уравнение:
Заменим для удобства тогда определитель характеристического уравнения имеет вид:
Решая определитель получим корни
Здесь Для второго дробного шага корни характеристического уравнения (здесь матрица
При 2.8. Уравнения газовой динамики и Навье-Стокса в комбинированных газодинамических переменных При построении газодинамических схем в качестве искомых переменных могут быть выбраны различные комбинации газодинамических параметров. Рассмотрим в качестве искомого вектора течения Выбор такого искомого вектора обусловлен следующим: 1. Уравнения газовой динамики и уравнения Навье-Стокса в этих переменных имеют более простую форму и просто реализуются. 2. Уравнения неразрывности и движения записываются в дивергентной форме. 3. Уравнение энергии может быть выбрано как в недивергентной, так и в дивергентной форме. Аппроксимация уравнения энергии в дивергентной форме приводит к построению консервативных разностных схем. Рассмотрим систему уравнений (см.[6]):
для которой
В случая системы газовой динамики:
а для случая системы уравнений Навье-Стокса:
Здесь Выберем разностную схему с весами для численного решения системы уравнений газовой динамики:
Здесь Схема нелинейная относительно искомого вектора
Тогда учитывая уравнение (41) получаем разностную схему
Рассмотрим приближенную факторизацию стабилизирующего оператора Разностная схема
аппроксимирует исходное уравнение (40) с тем же порядком, что и основная схема, но проще в реализации. Стабилизирующий оператор 1) безусловно устойчивой при соответствующем выборе значения параметра α, 2) могла быть реализована скалярными прогонками, 3) требовала минимального числа арифметических операций при своей реализации. Построить расщепление матрицы
Для численной реализации схемы (42) используется схема в дробных шагах или эквивалентная ей схема типа стабилизирующей поправки.
Рассмотрим решение по схеме (43) на каждом дробном шаге. На первом дробном шаге матрица разностные уравнения системы могут быть решены независимо друг от друга. Из первого уравнения системы находим значения переменной На втором дробном шаге решаем систему:
Из последнего уравнения системы выражаем значения давления на верхнем временном слое Можно показать, что разностная схеме безусловно устойчива при Дивергентный стабилизирующий оператор Покажем как для системы уравнений газовой динамики строятся безусловно устойчивые разностные схемы, реализуемые скалярными прогонками, если стабилизирующий оператор Рассмотрим систему:
где уравнение состояния Здесь Для решения системы воспользуемся следующей схемой с весами
которая аппроксимирует исходную систему с порядком Для получения линейной схемы проводим ее линеаризацию, относительно вектора
Здесь
Линеаризованная разностная схема:
аппроксимирует уравнение (44) с порядком
строим новую разностную схему где оператор Рассмотрим численную реализацию схемы методом дробных шагов:
На первом дробном шаге решается следующая система разностных уравнений:
Уравнения могут быть решены независимо друг от друга скалярными прогонками или по неявной схеме бегущего счета. На втором дробном шаге разностные уравнения:
решаются в следующем порядке. Исключаем 2.9. Схема с несогласованным стабилизирующим оператором При аппроксимации дифференциальных операторов вида Рассмотрим систему уравнений Навье-Стокса для сжимаемого теплопроводного газа записанную в следующем недивергентном виде.
Для ее аппроксимации выберем факторизованную разностную схему
со стабилизирующем оператором Здесь разностные операторы
Заметим, что m = Схема (47) на каждом дробном шаге решается
порядок аппроксимации членов оператора правой части. Определение. Оператор Рассмотрим разностную схему с несогласованным оператором при Покажем ее безусловную устойчивость для уравнений газовой динамики. В этом случае характеристическое уравнение схемы следующее:
где Один из корней характеристического уравнения равен
Два других оставшихся корня находим при
Таким образом, разностная схема (47) безусловно устойчива при
оператора. В многомерном случае схема приближенной факторизации с несогласованным стабилизирующим оператором становится условно устойчивой. 2.10. Схемы для решения стационарных задач При решении стационарных задач уравнений газовой динамики и Навье-Стокса используется два подхода: 1) непосредственное интегрирование системы стационарных уравнений, 2) интегрирование некоторой аппроксимирующей системы, решение которой стремится к решению исходной стационарной системы. Использование первого подхода приводит, в одномерном случае, к интегрированию систем нелинейных обыкновенных дифференциальных уравнений. В многомерном случае получается уже система уравнений в частных производных, тип которых зависит от режима течений. Как правило, для уравнений газовой динамики при сверхзвуковом течении - система гиперболического типа, а при дозвуковом – эллиптическая. Для параболизированных систем уравнений Навье-Стокса – системы параболического или эллиптического типов соответственно. Решение уравнений, особенно эллиптического типа, представляет значительные трудности. Поэтому для решения стационарных систем экономичнее использовать второй подход, основанный на итерационных методах. В уравнения добавляют итерационное слагаемое, временной параметр Такой метод хорош и тем, что он используется для любого типа течений. Рассмотрим применение этого метода на примере модельных уравнений. Для решения уравнения
с заданными граничными условиями воспользуемся следующей итерационной схемой (
При сходимости итераций (когда Итерационная схема (49) аппроксимирует (48) уже при установлении, а на промежуточных итерациях схема аппроксимирует другое уравнение. Действительно, если к числителю дроби, стоящей в правой части схемы (49) прибавить и отнять выражение
которая на каждом промежуточном шаге схема аппроксимирует уравнение:
Схема (49) безусловно устойчива. Устойчивость исследуем методом гармоник. При решении характеристического уравнения
Получаем, что Расчет по схеме (49) проводится по явной формуле:
Можно строить модификации схемы (49), которые тоже являются безусловно устойчивыми, например схема:
Здесь численный счет ведется по неявной схеме бегущего счета. В работе (см.[15]) предложена следующая схема для решения уравнения теплопроводности с использованием метода расщепления:
Переписывая схему (50) в виде
и после исключения промежуточного слоя приходим к разностному уравнению
Полученная схема аппроксимирует при установлении уравнение (48) со вторым порядком точности по времени и является безусловно устойчивой. Каждое уравнение системы (51) реализуется по схеме бегущего счета: первое уравнение – справа налево, а второе наоборот слева направо. Рассмотрим итерационную схему решения и нелинейного уравнения
Добавляем итерационное слагаемое
При установлении схема аппроксимирует уравнение (52) с порядком
2.11. Несколько замечаний для многомерных уравнений Для численного решения многомерных уравнений, построение разностной схемы усложняется (если использовать явные разностные схемы, то, как правило, ухудшается условие устойчивости), например, для уравнения переноса: – в одномерном случае: –в двухмерном случае: Хотя реализация схем сильно не усложняется. Хуже для неявных разностных схем. Схемы в этом случае становятся неэкономичными или условно устойчивыми, или реализуются матричными прогонками. На основе схем расщепления можно построить экономичную разностную схему. Для многомерных систем уравнений строится цепочка задач меньшей размерности, а затем эта цепочка исследуется.
Заключение
Основные методы теории разностных схем апробируются на задачах прикладной механики. Показано, как применяя разностный подход можно численно исследовать реальные физические модели. При изложении материала использовались разделы вычислительной механики, в частности аэродинамики, а также раздел механики жидкости и газа. Контрольные вопросы ко второй главе: 1. Явные разностные схемы для модельных уравнений. 2. Безусловно устойчивые разностные схемы для уравнений. 3.Методы построения схем повышенного порядка аппроксимации. 4. Схема с весами для системы уравнений газовой динамики. 5. Схемы расщепления по физическим процессам. 6. Схема приближенной факторизации. 7. Разностные схемы для полной системы уравнений Навье – Стокса дивергентного вида. 8. Понятие о монотонных разностных схемах. 9. Схемы для одномерных систем уравнений газовой динамики и Навье – Стокса, записанных в недивергентной форме. 10. Уравнения газовой динамики и Навье – Стокса в комбинированных переменных. 11. Схемы с несогласованным стабилизирующим оператором. 12. Схемы для стационарных задач.
Практическое задание ко второй главе:
1. Исследовать порядок аппроксимации и устойчивость следующих разностных схем линейных одномерных уравнений газовой динамики:
где Ответ: схема условно-устойчивая.
2. где Ответ: безусловно-устойчивая.
3. где Ответ: условно-устойчивая. Безусловно-устойчивая лишь для сверхзвуковых течений
|

 может невырожденным преобразованием приведена к диагональному виду
может невырожденным преобразованием приведена к диагональному виду  . Существует и обратное преобразование
. Существует и обратное преобразование  .
. . Ее можно представить в виде суммы неотрицательной и неположительной матриц. Например
. Ее можно представить в виде суммы неотрицательной и неположительной матриц. Например
 .
. :
: (34)
(34) и неположительного вектора
и неположительного вектора  .
.

 и
и  .
. выбирают в переменных
выбирают в переменных  , что позволяет решать независимо уравнение неразрывности от остальных уравнений системы. Матрица В имеет очень простую структуру. Для системы уравнений Навье-Стокса вектор состояния
, что позволяет решать независимо уравнение неразрывности от остальных уравнений системы. Матрица В имеет очень простую структуру. Для системы уравнений Навье-Стокса вектор состояния  .
. можно записать в виде:
можно записать в виде: (35)
(35) и
и  - квадрат скорости звука.
- квадрат скорости звука. , тогда
, тогда . (36)
. (36)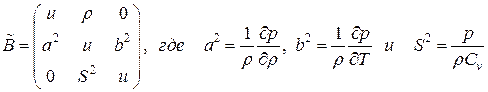 .
. .
. (37)
(37) , где
, где  порядок разностной производной.
порядок разностной производной. ,
,
 операторами
операторами  знаки в конвективных членах и члене с давлением выбираются согласованно.
знаки в конвективных членах и члене с давлением выбираются согласованно. и уравнения (37) видно, что для нахождения решения системы (36) используются векторные прогонки, а для нахождения решения системы (35) используется векторная прогонка для вычисления координат
и уравнения (37) видно, что для нахождения решения системы (36) используются векторные прогонки, а для нахождения решения системы (35) используется векторная прогонка для вычисления координат  и
и 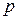 , а затем можно пересчитать
, а затем можно пересчитать  из уравнения неразрывности методом сквозного счета.
из уравнения неразрывности методом сквозного счета.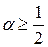 .
.
 в разностную схему, где
в разностную схему, где  и получаем следующее характеристическое уравнение:
и получаем следующее характеристическое уравнение: .
. имеем
имеем В операторном виде это уравнение:
В операторном виде это уравнение: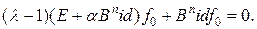 Его определитель
Его определитель

 и
и  , тогда
, тогда .
.
 или
или .
.  имеем
имеем  .
.
 :
: , (38)
, (38)
 по формуле
по формуле .
. . Здесь матрицы
. Здесь матрицы
 учитывает конвективные слагаемые уравнения, а оператор
учитывает конвективные слагаемые уравнения, а оператор  учитывает слагаемое с давлением в уравнении движения и слагаемые вида дивергенции скорости в уравнениях неразрывности и энергии.
учитывает слагаемое с давлением в уравнении движения и слагаемые вида дивергенции скорости в уравнениях неразрывности и энергии.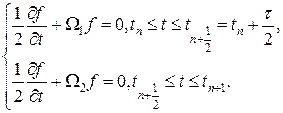
 (39)
(39)
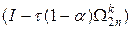 , а второе справа на оператор
, а второе справа на оператор  , после сложения получаем:
, после сложения получаем:
 и
и  некоммутативные, поэтому исключит дробный шаг в общем случае не удается.
некоммутативные, поэтому исключит дробный шаг в общем случае не удается. , то решение разностного уравнения для любой из компонент вектора
, то решение разностного уравнения для любой из компонент вектора  может быть получено по неявной схеме бегущего счета для двухточечных разностных уравнений
может быть получено по неявной схеме бегущего счета для двухточечных разностных уравнений
 , то счет ведется слева направо (верхний знак в формуле) и при
, то счет ведется слева направо (верхний знак в формуле) и при  справа налево (нижний знак в формуле).
справа налево (нижний знак в формуле). ,
, .
. . При симметричной аппроксимации (
. При симметричной аппроксимации (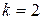 ) прогонка хорошо обусловлена лишь при
) прогонка хорошо обусловлена лишь при  . В случае плохой обусловленности
. В случае плохой обусловленности  решаем уравнение методом немонотонной прогонки.
решаем уравнение методом немонотонной прогонки. , где
, где  , то решение разностного уравнения может быть получено по неявной схеме бегущего счета для трехточечных разностных уравнений или скалярными пятиточечными прогонками, если скорость знакопеременная функция.
, то решение разностного уравнения может быть получено по неявной схеме бегущего счета для трехточечных разностных уравнений или скалярными пятиточечными прогонками, если скорость знакопеременная функция.
 и
и  из последнего уравнения, получаем разностное уравнение для нахождения значения скорости на
из последнего уравнения, получаем разностное уравнение для нахождения значения скорости на 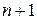 временном слое. Это уравнение решается трехточечной скалярной прогонкой (при k=1). Значения для плотности и энергии на
временном слое. Это уравнение решается трехточечной скалярной прогонкой (при k=1). Значения для плотности и энергии на 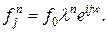 Тогда
Тогда 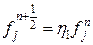 ,
, 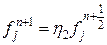 или
или  . В силу неравенства
. В силу неравенства  и двухслойности разностных схем достаточно показать устойчивость схемы для каждого дробного шага.
и двухслойности разностных схем достаточно показать устойчивость схемы для каждого дробного шага.
 .
. и
и 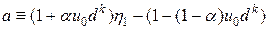 ,
, .
. Коэффициент
Коэффициент  зависит от способа аппроксимации, а именно:
зависит от способа аппроксимации, а именно:
 Получаем, что
Получаем, что  при
при  не является диагональной) равны
не является диагональной) равны ,
, скорость звука и
скорость звука и  , где
, где  при
при  и
и  =
=  при
при  .
.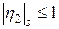 . Таким образом,
. Таким образом,  , т.е.разностная схема безусловно устойчива при
, т.е.разностная схема безусловно устойчива при  .
. (40)
(40) и
и .
. ,
, .
.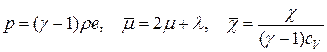 .
. . (41)
. (41) .
. . Линеаризуем вектор
. Линеаризуем вектор 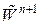 относительно вектора
относительно вектора  .
. 
 линейную относительно функций на верхнем временном слое и аппроксимирующую систему (40) с порядком
линейную относительно функций на верхнем временном слое и аппроксимирующую систему (40) с порядком  .
. , где
, где  .
. (42)
(42) выбирается так, чтобы разностная схема (42) была:
выбирается так, чтобы разностная схема (42) была: на матрицы
на матрицы  и
и  можно четырьмя различными способами для выполнения условий 1) и 2), но для выполнения третьего условия выбираем следующий вид расщепленных операторов:
можно четырьмя различными способами для выполнения условий 1) и 2), но для выполнения третьего условия выбираем следующий вид расщепленных операторов: и
и  .
. (43)
(43)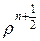 , а затем из второго и третьего уравнений системы независимо друг от друга находим значения переменных
, а затем из второго и третьего уравнений системы независимо друг от друга находим значения переменных  и
и 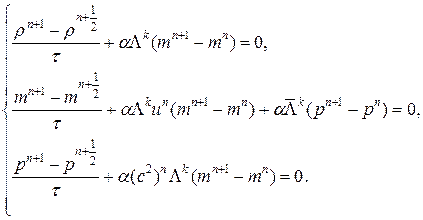
 и подставляем во второе уравнение системы, которое затем решается скалярными прогонками. Находим значения переменной
и подставляем во второе уравнение системы, которое затем решается скалярными прогонками. Находим значения переменной  . Из первого и третьего уравнений системы определяем остальные неизвестные параметры.
. Из первого и третьего уравнений системы определяем остальные неизвестные параметры. , (44)
, (44) .
. .
. ,
, относительного верхнего временного слоя.
относительного верхнего временного слоя. и
и  .
. и
и  .
. , где
, где  .
. , (45)
, (45)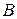 на сумму двух операторов:
на сумму двух операторов: и
и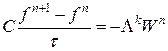 ,
,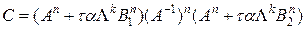 получен приближенной факторизацией стабилизирующего оператора схемы (45). Схема аппроксимирует исходную систему уравнений (44) с тем же порядком
получен приближенной факторизацией стабилизирующего оператора схемы (45). Схема аппроксимирует исходную систему уравнений (44) с тем же порядком 


 и
и  из уравнения движения и получаем относительно
из уравнения движения и получаем относительно  разностное уравнение.
разностное уравнение. несимметричными разностными операторами
несимметричными разностными операторами  получаются разностные схемы, которые реализуются пятиточечными скалярными прогонками. Для получения стационарного решения методом установления можно использовать схемы, в которых порядок аппроксимации членов в стабилизирующем операторе
получаются разностные схемы, которые реализуются пятиточечными скалярными прогонками. Для получения стационарного решения методом установления можно использовать схемы, в которых порядок аппроксимации членов в стабилизирующем операторе 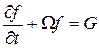 . (46)
. (46) (47)
(47)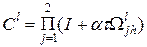 .
.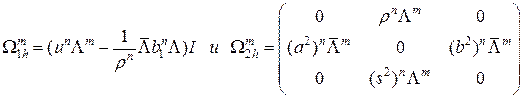 , где
, где и
и  .
. .
. -точечными прогонками и погрешность ее аппроксимации есть
-точечными прогонками и погрешность ее аппроксимации есть , а при установлении
, а при установлении  . Здесь
. Здесь  – порядок аппроксимации членов стабилизирующего оператора, а
– порядок аппроксимации членов стабилизирующего оператора, а 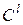 называется согласованным, если
называется согласованным, если  и несогласованным, если
и несогласованным, если  .
. . На каждом дробном шаге ее решение может быть получено трехточечной прогонкой и при установлении схема имеет порядок аппроксимации
. На каждом дробном шаге ее решение может быть получено трехточечной прогонкой и при установлении схема имеет порядок аппроксимации  . Эта схема по-прежнему остается безусловно устойчивой, но запас устойчивости ее уменьшается.
. Эта схема по-прежнему остается безусловно устойчивой, но запас устойчивости ее уменьшается.
 и
и  .
. . Тогда
. Тогда  , если
, если 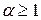 .
. в предельных случаях, когда
в предельных случаях, когда  – гиперзвуковое течение. В этом случае корни характеристического уравнения
– гиперзвуковое течение. В этом случае корни характеристического уравнения  . И во втором случае, когда
. И во втором случае, когда 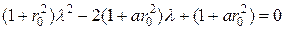 , где
, где . Его корни равны
. Его корни равны  .
. является итерационным, и методом установления решается система уравнений, которая сходится к исходной системе.
является итерационным, и методом установления решается система уравнений, которая сходится к исходной системе. (48)
(48) – номер итерации)
– номер итерации) (49)
(49) ) схема (49) при установлении аппроксимирует уравнение (48) с порядком
) схема (49) при установлении аппроксимирует уравнение (48) с порядком  , то получим следующую схему:
, то получим следующую схему:
 .
.
 , так как
, так как  .
. .
. ,
, (50)
(50) (51)
(51) . Здесь
. Здесь  .
. , где
, где  . (52)
. (52) .
. может численно решена по схеме бегущего счета.
может численно решена по схеме бегущего счета. ,
, , учитывая
, учитывая  .
.
 и
и  .
. ,
,  , где
, где 

 и
и 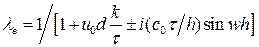 ,
, 
 и
и  – сопряженный оператор.
– сопряженный оператор.



