Эффект Доплера, его исследование и значение для наукиЗависимость частоты волнового импульса от скорости при движении источника волн относительно наблюдателя называют эффектом Доплера. Эффект Доплера имеет место для всех типов волн — звуковых в атмосфере, упругих в твердом теле, волн на воде, световых волн. Австрийский физик и астроном К.Доплер обнаружил эту зависимость в 1842 г. Многие слышали, как меняется звук свистка проносящегося мимо платформы поезда. Первое подтверждение эффекта было получено для акустических волн в опытах голландского физика с группой музыкантов на железной дороге (1845). Часть группы разместилась на платформе, двигавшейся с известной скоростью вдоль перрона, где находились остальные, воспринимая их музыку. Затем музыканты поменялись ролями. Данные, полученные от непосредственных впечатлений участников опыта, хорошо укладывались в формулу Доплера. Но эффект Доплера можно не только «слышать», но и «видеть», хотя бы в ванне или пруду (рис. 3.6). Периодически погружая палец в воду,
чтобы на поверхности образовались волны, равномерно перемещайте его в одном направлении. Следуя друг за другом, гребни волн в направлении движения пальца будут сгущаться, т. е. длина волны станет меньше обычной, в направлении назад — больше. Период волны, излучаемой неподвижным источником, равен наблюдателя. Тогда длина волны, воспринимаемая неподвижным наблюдателем, равна
Поскольку системы отсчета, связанные с источником и наблюдателем, инерциальны,
Здесь знак «-» соответствует движению источника от наблюдателя, а знак «+» — движению источника к наблюдателю. Таким образом, частота волны, регистрируемая наблюдателем, отличается от частоты волны, излучаемой источником, на величину, равную доплеровскому сдвигу частоты:
Пусть теперь источник движется со скоростью w. Тогда относительная длина волны, воспринимаемая наблюдателем, равна
где u-w — относительная скорость движения источника и наблюдателя. Отсюда частота волны, воспринимаемая наблюдателем, равна
Для доплеровского сдвига частоты получаем
Следовательно, доплеровский сдвиг частоты равен частоте волны в системе отсчета источника, умноженной на коэффициент, равный относительной скорости источника и наблюдателя, деленной на скорость распространения волны в среде. Измерение доплеровского смещения в спектрах позволяет с большой точностью и, не возмущая измерением движение и систему, определить скорости движущихся объектов. Французский физик А.Физо предложил (1848) использовать эффект Доплера для измерения радиальной составляющей скорости звезд по сме-
Академик А. А. Белопольский считал, что нужно провести проверку в земных условиях, поскольку неизвестны условия излучения в Космосе. С этой целью в 1894 г. он разработал установку, состоявшую из двух колес, к каждому из них в виде лопастей прикреплялись 8 плоских зеркал. Зеркала обоих колес были строго параллельны и вращались с постоянной скоростью. Съемки проводились при неподвижных зеркалах и при вращающихся с частотой 32 — 44 об/с (это соответствовало перемещению изображения со скоростью 240 — 330 м/с). Обработка результатов дала хорошее совпадение по числу оборотов колес и доплеровскому смещению. Вращение производилось в обе стороны поочередно. Опыт длился всего 1 ч, но он бьш наиболее убедительным в применении эффекта Доплера к свету. Эффект Доплера как основной в оптике движущихся сред сыграл решающую роль в обосновании СТО. Физо поставил (1851) классический эксперимент по определению увлечения эфира движущейся Землей. Он заставил интерферировать два луча света, проходящих столб воды: один в направлении течения, а другой — против него. Если эфир увлекается, то полосы должны смещаться по отношению к положению, соответствующему неподвижной воде. К тому же результату пришли Э. Кеттлер (1871) и Май-кельсон и Морли (1886) — эфир движется вместе с Землей. Ранее Майкельсон пытался обнаружить «эфирный ветер» при движении Земли в эфире, посылая световые лучи по взаимно перпендикулярным путям и заставляя их интерферировать. Хотя линейная скорость Земли (29, 7 км/с) много меньше скорости света и установка позволяла засечь и в 100 раз меньший эффект, опыт дал отрицательный результат. Опыты, показывавшие увлечение эфира, противоречили объяснению явления аберрации (от лат. aberratio — отклонение), требовавшей неподвижности эфира. Это противоречие было разрешено отказом от эфира и созданием СТО. Когда картина мира стала меняться на квантовую, возникла необходимость в ином объяснении эффекта Доплера. Как отмечал известный немецкий физик А. Зоммерфельд, казалось почти невозможным трактовать эффект Доплера как обусловленный взаимным сближением или удалением волновых поверхностей. В 1922 г. один из создателей квантовой механики австрийский физик-теоретик Э. Шредингер дал такое обобщение формулы Доплера для частоты на случай больших скоростей. Метод для измерений скоростей звезд и галактик, основанный на эффекте Доплера, получил в астрономии наиболее впечатляющее применение. Спектры галактик слабы, измерения достаточно трудны. Американский астроном В.Слайфер с помощью мощного спектрографа, соединенного с телескопом, измерил доплеровский сдвиг в спектре туманности Андромеды (1912), затем — еще в тринадцати спиральных галактиках. Скорости большинства из них были направлены в противоположную сторону от Земли и составляли до 1800 км/с. К 1925 г. Слайфер измерил лучевые скорости еще 45 спиральных галактик, и все они, кроме нескольких ближайших, удалялись, а скорость удаления почему-то возрастала по мере уменьшения их яркости, будто они разбегались от Млечного Пути во всех направлениях с возрастающей скоростью. Чтобы согласовать это с однородным распределением галактик в пространстве, пришлось считать, что это — однородное расширение. Но тогда их лучевая скорость (проекция скорости на луч зрения) должна быть пропорциональна расстоянию до них. Так, если галактика выглядит в 100 раз слабее, значит, она в 10 раз дальше. Галактики из списка Слайфера имели лучевую скорость 1800 км/с, а расположенные в 10 раз дальше — 180000 км/с (половина значения скорости света).
Для формулирования закона пришлось искать возможность определения расстояния до галактик независимым образом. Параллакс для ближних звезд можно измерить по методу, предложенному еще Фалесом, для далеких — искать некий индикатор расстояний. Американский астроном Г.Левитт обратила внимание на четкую зависимость периода цефеид от яркости (рис. 3.7). Цефеиды — наиболее яркие звезды в небольшой ближайшей к нам галактике — Малом Магеллановом Облаке. Название они получили от типичной цефеиды — дельта звезды созвездия Цефея. Датский астроном Э. Герцшпрунг сразу оценил идею Левитт и отка-либровал выведенную ею зависимость период-яркость в период-светимость и определил расстояние до этой галактики в 200 тыс. св. лет. Хаббл с помощью 100-дюймового телескопа обнаружил цефеиды в нескольких галакти-
ках и смог оценить расстояние до них. Так Хаббл в 1929 г. вывел прямую линию на графике зависимости скоростей далеких галактик от расстояния до них (рис. 3.8). Итак, скорости удаления v галактик возрастают пропорционально расстоянию до них: v= Н r, где Н — постоянная Хаббла. Сейчас считается, что H = 75 км/(с • Мпк). Расширение Вселенной — самое грандиозное из известных в настоящее время явлений природы. Если допустить, что оно и раньше происходило теми же темпами, то можно оценить, когда же началось расширение. Этот промежуток времени составляет 13 — 20 млрд лет. Таким образом, смещение спектральных линий из-за эффекта Доплера привело к новой картине расширяющейся Вселенной. Явление резонанса. Резонансы в движении планет Явление резонанса — это резкое возрастание амплитуд вынужденных колебаний, происходящее при совпадении частоты вынуждающей силы с собственной частотой системы или при приближении к ней. Явление имеет наиболее простой характер, если внешнее воздействие не меняет колебательных свойств системы и свойства системы, со своей стороны, не меняют внешнего воздействия. Если отношения частот колебаний кратны отношению целых чисел, говорят, что они находятся в резонансе. При этом если взаимодействие тел поддерживает кратность частот, то резонанс устойчив. Вообще свойства резонанса частот обеспечивают устойчивость вращений и обращений в Солнечной системе. Вращение Луны резонансно ее обращению. В середине XVII в. немецкий математик Д.Тициус для ряда из расстояний планет до Солнца нашел правило: S = 0, 4 + 0, 3 • 2n, n =1, 2, 3,..., где и — номера планет в Солнечной системе. Астроном И.Э.Боде дал разъяснения, и получилось правило расстояний Тициуса—Боде. Отличие от реальности было порядка 2, 4 %. В 1956 г. астроном В. Чистяков нашел другую гармонию: натуральные логарифмы больших полуосей планет ложатся на прямую линию. Есть попытки выразить согласованность через «золотую пропорцию», через числа Фибоначчи. Поиски скрытого смысла закономерностей строения Солнечной системы про- должаются, в этом отражается единство природы и единство науки. Синхронизация вращающихся тел в технике заставляет вращаться с одинаковыми или кратными скоростями несколько роторов, связанных малыми силами. При этом между вращениями устанавливаются определенные фазовые соотношения. Подобное можно ожидать и в Солнечной системе, и в регуляризации излучения звезд. Многие миллионы лет эволюционировало газопылевое облако, вращаясь вокруг Солнца. Ритмы этих вращений сказывались в формировании комочков материи, вокруг которых группировались другие, давшие начало планетам. Вращаются все планеты и их спутники, и угловая скорость их вращения пропорциональна массе. Вероятно, это — следствие образования планет из одной туманности. Столкновения частиц сильнее происходили в центре масс системы, куда собирался почти весь газ первоначальной туманности — образовалось Солнце. Но почти весь момент импульса оказался сосредоточенным в планетах. Когда на Солнце начались термоядерные реакции, оно стало звездой, легкие газы под действием его излучения собрались на периферии вращающейся туманности. Так образовались большие планеты — газовые шары. Планеты же земной группы образованы из более твердого вещества. По закону сохранения момента импульса при сжатии вещества вращающейся туманности в плотные шары скорость вращения должна расти. Поэтому у планет-гигантов скорость вращения оказывается больше. И зависимость угловой скорости вращения от масс планет почти линейна. Отклонения связаны с замедлением, вызванным тормозящим действием спутников планет. В системе Земля—Луна отношение масс составляет всего Плутона и его спутника Харона). Хотя в Солнечной системе есть спутники и более близкие к своим планетам, но солнечные затмения на Земле особенные — угловые диаметры Солнца и Луны почти равны друг другу, и поэтому бывают полные солнечные затмения. Под действием притяжения Луны земная орбита испытывает колебания, амплитуда которых определяется
го уширения фигуры Земли создало пару сил, стремящуюся развернуть Землю так, чтобы ее экватор совпал с плоскостью эклиптики. Если бы Луны не было, земная ось все равно испытывала бы прецессию под действием Солнца и планет, но ее период прецессии был бы около 100 тыс. лет, а Луна меняет его. Еще больше сказывается близость Луны в явлении приливов и отливов. Приливы вызываются Солнцем и Луной не только в водной оболочке Земли. Под их влиянием даже твердая Земля несколько удлиняется — до 30 см. Земля тоже «вытягивает» Луну на 40 см. Взаимное расположение Солнца и Луны меняет величину приливов. Если их приливные действия складываются (во время полнолуния или новолуния), то приливы большие — сизигийные (от греч. syzygia — соединение, пара), если Луна находится в первой или третьей четверти, то приливы существенно меньше и называются квадратурными. Из-за приливных сил Луна обращена к Земле одной стороной, ее период вращения вокруг своей оси сравнялся с ее «годом». Почти в той же ситуации находится Меркурий: его сутки равны 59 земным, и он успевает всего три раза обернуться вокруг своей оси за два оборота вокруг Солнца, т. е. за свои сутки проходит 2/3 своего годового пути. На Венере вращение происходит тоже медленно. Существует гипотеза, что Меркурий и Венера раньше вращались по одной орбите. У Меркурия наибольшая вытянутость орбиты, и Солнце, расположенное в фокусе эллипса, значительно смещено от центра, поэтому скорость у Меркурия в перигелии в 1, 52 раза выше, чем в афелии. Оценим период между двумя восходами Солнца на Меркурии
щен к Солнцу то одним боком, то другим, а в афелии прогреваются его полюсы. У Венеры ось вращения почти перпендикулярна плоскости ее орбиты, поэтому можно приписать знак минус ее периоду вращения: Р = = -243, 16 сут. Она вращается медленнее и в противоположную сторону, в отличие от других планет, кроме Урана. Для них момент орбитального импульса близок к моменту импульса собственного вращения. Периоды вращения Р иобращения Т Венеры связаны с периодом обращения Земли Т 3следующим равенством: сближения на минимальное расстояние Венеры с Землей (соединений планет): систему отсчета неподвижной Земли, и теперь период сближения солнечные сутки Венеры. Поскольку время восход Земли ровно 4 раза. Значит, в моменты соединений Венера повернута к Земле всегда одной стороной (в центре этой «нашей» стороны находится высокая гора — вулкан Максвелл). Кроме того, периоды обращения Венеры и Земли соотносятся как 8: 13, т.е. за 8 лет происходит 13 оборотов Венеры вокруг Солнца и 5 соединений с Землей. Не только Венера, а вся система Солнце—Венера—Земля ориентируется по отношению к звездам одним из пяти способов, а не произвольно. И эта упорядоченная ситуация повторяется (рис. 3.9). Большие планеты при вращении имеют свои особенности, показывающие, что они — газовые шары. Планеты земной группы вращаются как твердые тела, тогда как скорости вращений планет-гигантов зависят от широты и, видимо, от глубины. Все эти кинематические особенности планет сказываются на их внутренней динамике и связаны с эволюцией планеты. Вопросыдля самопроверки и повторения 1. Сформулируйте основные законы и понятия классической механики материальной точки. Как моделируется система, состоящая из двух и более материальных точек? Приведите примеры задач, в которых можно считать Землю материальной точкой, а в каких — нельзя. 2. Сформулируйте законы сохранения импульса и момента импульса в классической механике и свяжите их с законом динамики Ньютона. Приведите примеры использования этих законов. Как они связаны со свойствами симметрии пространства-времени и почему фундаментальны? 3. Дайте представление о модели гармонического осциллятора и использовании этой модели. Что такое «когерентность», «резонанс», «поляризация»? Объясните, почему Луна обращена к Земле одной стороной. 4. В чем суть законов Кеплера? Поясните их связь с законом всемирного тяготения. Насколько применима модель, принятая Ньютоном? И как она была уточнена? 5. Поясните понятия «энергия» и «сила», укажите на связь между ними. Какие виды энергии вы знаете? В каких системах энергия сохраняется, как закон сохранения энергии связан со свойствами симметрии пространства-времени? 6. Приведите доказательства справедливости и применимости закона всемирного тяготения на Земле, в Солнечной системе и за ее пределами. Какие явления, произошедшие в последние годы и подтверждающие этот закон, вы можете привести? 7. Поясните понятия «момент силы» и «момент импульса». Как изменяются кинетическая, полная и потенциальная энергии планеты при ее движении вокруг Солнца? В какое время линейная скорость движения Земли по орбите наибольшая и почему? 8. Опишите, как будет меняться вес тела при движении его от поверхности Земли к Луне. Объясните причины возникновения приливов на Земле и особенности наблюдения за затмениями Луны и Солнца. 9. В чем состоит эффект Доплера и какова его роль в исследовании звезд, Вселенной? 10. Как реализовались в построении науки о движении материи дедук Глава 4 КОНЦЕПЦИИ КЛАССИЧЕСКОЙ ТЕРМОДИНАМИКИ И СТАТИСТИЧЕСКОЙ МЕХАНИКИ Проблема соотношения динамического и статистического подходов в описании природы — одна из актуальных в философии современного естествознания. Отношение к ней изменялось в ходе развития науки. Сначала стремились обосновать молекулярно-кинетическую теорию строения вещества с позиций классической механики. Но после установления атомного строения и понимания большей глубины статистической трактовки основных законов проблема несколько утратила свою остроту. В неклассической трактовке она вновь стала актуальной в связи с необходимостью построения теории элементарных частиц, выходящей за рамки квантовой теории поля. В ней отражено взаимодействие необходимого и случайного, пронизывающего все явления природы. И любые законы, касающиеся сложных форм движения материи, связаны теснейшим образом с фундаментальными проблемами диалектики детерминизма и индетерминизма, случайного и необходимого, динамического и статистического, как и принципа причинности.
|


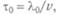 где
где 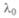 — длина волны, излучаемой покоящимся источником, v — скорость волны в среде. Пусть источник движется со скоростью и в сторону
— длина волны, излучаемой покоящимся источником, v — скорость волны в среде. Пусть источник движется со скоростью и в сторону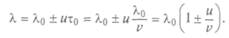
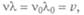 где
где 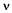 — частота волны в системе отсчета наблюдателя,
— частота волны в системе отсчета наблюдателя, 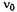 - частота волны в системе отсчета источника. Отсюда
- частота волны в системе отсчета источника. Отсюда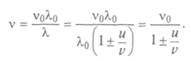
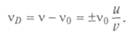
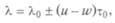

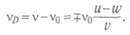

 щению спектральных линий (эффект Доплера—Физо). Он заметил, что в линейчатых спектрах можно измерять смещение. В 1867 г. английский астроном У. Хеггинс измерил доплеровское смещение водородной линии в спектре Сириуса и сравнил его с той же линией в спектре, полученном в лаборатории. Он заключил, что скорость звезды относительно Земли равна 66, 6 км/с, а относительно Солнца — 47, 3 км/с. Но для доказательства применимости эффекта Доплера к свету нужно было найти объект, скорость которого можно было бы измерить и другим способом. В 1871 г. немецкий астроном Г. Фогель измерил доплеровские смещения для двух точек солнечного экватора, находящихся на краях диска, и определил их линейную скорость — 2 км/с, что совпадало с результатом, полученным по движению пятен. Затем определили скорости вращения планет, колец Сатурна, звезд вокруг своей оси, ядер и хвостов комет.
щению спектральных линий (эффект Доплера—Физо). Он заметил, что в линейчатых спектрах можно измерять смещение. В 1867 г. английский астроном У. Хеггинс измерил доплеровское смещение водородной линии в спектре Сириуса и сравнил его с той же линией в спектре, полученном в лаборатории. Он заключил, что скорость звезды относительно Земли равна 66, 6 км/с, а относительно Солнца — 47, 3 км/с. Но для доказательства применимости эффекта Доплера к свету нужно было найти объект, скорость которого можно было бы измерить и другим способом. В 1871 г. немецкий астроном Г. Фогель измерил доплеровские смещения для двух точек солнечного экватора, находящихся на краях диска, и определил их линейную скорость — 2 км/с, что совпадало с результатом, полученным по движению пятен. Затем определили скорости вращения планет, колец Сатурна, звезд вокруг своей оси, ядер и хвостов комет.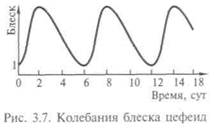




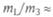 1/81, 3, и они тормозили друг друга. Среднее расстояние до Луны
1/81, 3, и они тормозили друг друга. Среднее расстояние до Луны 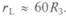 У других планет спутники много легче (кроме
У других планет спутники много легче (кроме = 4700 км. Поэтому орбита Земли несколько «волнообразна», и в каждое полнолуние (Солнце и Луна находятся по разные стороны от Земли) мы ближе к Солнцу на 1, 5 R 3, чем в предыдущее. Это колебание мало по сравнению с вытянутостью орбиты Земли, но меняет движение Луны — совокупность ее орбит за время прецессии Земли (с периодом 26 тыс. лет) представляет некий тор. Его воздействие на Землю равно усредненному за это время действию Луны. Сплюснутость Земли, составляющая всего 1/300, достаточна для того, чтобы притяжение этим «бубликом» экваториально-
= 4700 км. Поэтому орбита Земли несколько «волнообразна», и в каждое полнолуние (Солнце и Луна находятся по разные стороны от Земли) мы ближе к Солнцу на 1, 5 R 3, чем в предыдущее. Это колебание мало по сравнению с вытянутостью орбиты Земли, но меняет движение Луны — совокупность ее орбит за время прецессии Земли (с периодом 26 тыс. лет) представляет некий тор. Его воздействие на Землю равно усредненному за это время действию Луны. Сплюснутость Земли, составляющая всего 1/300, достаточна для того, чтобы притяжение этим «бубликом» экваториально-


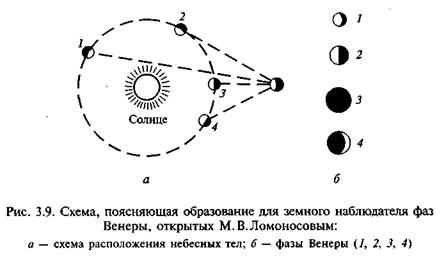
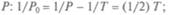
 Получается, что солнечные сутки на Меркурии втрое больше звездных и вдвое больше периода обращения. Если нарисовать «годовой путь» Меркурия, то видно, что в перигелии Меркурий обра-
Получается, что солнечные сутки на Меркурии втрое больше звездных и вдвое больше периода обращения. Если нарисовать «годовой путь» Меркурия, то видно, что в перигелии Меркурий обра-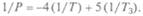 Вычислим период
Вычислим период 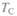
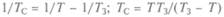 = 583, 92 сут. Перейдем в
= 583, 92 сут. Перейдем в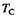 окажется временем возвращения Венеры к Земле после оборота ее вокруг Солнца. Полученное число 583, 92 земных суток соответствует пяти суткам на Венере, т.е. за время между сближениями Венеры с Землей над горизонтом Венеры Солнце взойдет всего пять раз. И
окажется временем возвращения Венеры к Земле после оборота ее вокруг Солнца. Полученное число 583, 92 земных суток соответствует пяти суткам на Венере, т.е. за время между сближениями Венеры с Землей над горизонтом Венеры Солнце взойдет всего пять раз. И  = 116, 8 — это
= 116, 8 — это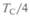 = 146, 0, то наблюдатель на Венере увидел бы за это
= 146, 0, то наблюдатель на Венере увидел бы за это


