Неравенство Чебышева
Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа Неравенство Чебышева справедливо как для дискретных, так и для непрерывных случайных величин. Неравенство Чебышева используют для вывода теоремы Чебышева. Пример 1.22. Используя неравенство Чебышева, оценить вероятность того, что случайная величина Х отклонится от своего математического ожидания не менее чем на 3 средних квадратических отклонения. Решение: По условию задачи
Задания для самостоятельной работы: 1. Используя неравенство Чебышева, оценить вероятность того, что 2. Дискретная случайная величина Х задана законом распределения:
Используя неравенство Чебышева, оценить вероятность того, что 1.2.3. Непрерывная случайная величина
|


 , не меньше, чем
, не меньше, чем  .
.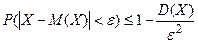
 , тогда
, тогда
 , если D(X)= 0, 004.
, если D(X)= 0, 004. .
.


