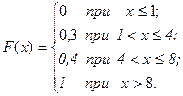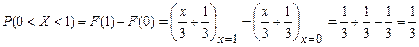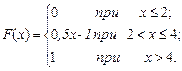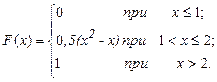Функция распределения вероятностей случайной величиныФункцией распределения называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина X примет значение, меньше х, т.е. F(x) – называют «интегральной функцией распределения». Функция обладает следующими свойствами: 1. 2. Функция распределения есть неубывающая функция своего аргумента: если x2> x1, то F(x2)> F(x1) Следствие 1. Следствие 2. 3. Если все возможные значения случайной величины Х принадлежат интервалу (a, b), то при Пример 1.23. Дискретная случайная величина Х задана законом распределения:
Найти функцию распределения и начертить ее график. Решение: если если если Если x> 8, то F(x)= 1. Итак, функция распределения аналитически может быть записана так:
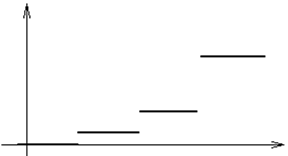
График функции приведен на рис. 3.
Рис. 3. Пример 1.24. Случайная величина Х задана функцией распределения:
Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (0, 1). Решение: Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале Положив a= 0, b= 1, получим:
Задания для самостоятельной работы: 1. Дискретная случайная величина задана законом распределения:
Найти функцию распределения и построить ее график. 2. Случайная величина Х задана функцией распределения:
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (2, 3). 3. Случайная величина Х задана функцией распределения:
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (1; 1, 5).
|

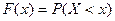 .
. – значение функции распределения принадлежит отрезку [0, 1].
– значение функции распределения принадлежит отрезку [0, 1].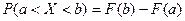
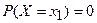 – вероятность того, что непрерывная случайная величина примет одно отдельно взятое значение.
– вероятность того, что непрерывная случайная величина примет одно отдельно взятое значение.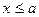 F(x)= 0, при
F(x)= 0, при  F(x)= 1.
F(x)= 1.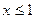 , то F(x)= 0;
, то F(x)= 0; , то F(x)= 0, 3;
, то F(x)= 0, 3;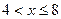 , то F(x)= 0, 4 – на этом интервале х принимает значение 1 с вероятностью 0, 3 и значение 4 с вероятностью 0, 1. Поскольку эти события несовместны, то по теореме сложения вероятностей 0, 3 + 0, 1 = 0, 4
, то F(x)= 0, 4 – на этом интервале х принимает значение 1 с вероятностью 0, 3 и значение 4 с вероятностью 0, 1. Поскольку эти события несовместны, то по теореме сложения вероятностей 0, 3 + 0, 1 = 0, 4