Групповая, внутригрупповая, межгрупповая и общая дисперсияГрупповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней:
где ni – частота значений xi; j – номер группы; Зная дисперсию каждой группы, можно найти их среднюю арифметическую. Внутригрупповой дисперсией называют среднюю арифметическую дисперсию, взвешенную по объемам групп:
где Nj – объем группы j; Зная групповые средние и общую среднюю, можно найти дисперсию групповых относительно общей средней. Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
где Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
где nj – частота значений xi; Пример 2.9. Найти групповые дисперсии, внутригрупповую дисперсию, межгрупповую дисперсию и общую дисперсию совокупности, состоящей из следующих двух групп:
Решение: 1. Найдем групповые средние: а) объем групп б) 2. Найдем групповые дисперсии:
3. Найдем внутригрупповую дисперсию:
4. Определим межгрупповую дисперсию: а) определим общую дисперсию:
б) используя групповые средние
5. Найдем общую дисперсию:
Замечание: найденная общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
Задание для самостоятельной работы: Найти групповые дисперсии, внутригрупповую дисперсию, межгрупповую дисперсию и общую дисперсию совокупности, состоящей из следующих двух групп:
2.3. Интервальные оценки. Доверительная вероятность. Доверительный интервал
Интервальной называют оценку, которая определяется двумя числами-концами интервала. Интервальные оценки позволяют установить точность и надежность оценок. Чем точнее оценка Поскольку статистические методы не позволяют категорически утверждать, что оценка Надежностью (доверительной вероятностью) оценки
Наиболее часто задают надежность, равную 0, 95; 0, 99; 0, 999. Неравенство
Тогда Доверительным называют интервал Пусть количественный признак Х генеральной совокупности распределен нормально, требуется оценить математическое ожидание а по выборочной средней
Для определения оценки используют:
Окончательно рассчитанная формула имеет вид:
Параметр t определяется из равенства Пример 2.10. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением Решение: 1. Из соотношения
2. Определим точность оценки:
3. Доверительный интервал
Таким образом Замечание. Если требуется оценить математическое ожидание с наперед заданной точностью
Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном
Доверительный интервал Пример 2.11. Количественный признак Х генеральной совокупности распределен нормально. По выборке объема n= 16 найдены выборочная средняя Решение: 1. Найдем 2. Найдем доверительные границы:
3. С надежностью 0, 95 неизвестный параметр а заключен в доверительном интервале:
Задания для самостоятельной работы: 1. Найти доверительный интервал для оценки с надежностью 0, 99 неизвестного математического ожидания а нормального распределения признака Х генеральной совокупности, если известны генеральное среднее квадратическое отклонение
б) б) 2. Найти минимальный объём выборки, при котором с надёжностью 0, 925 точность оценки математического ожидания нормально распределённой генеральной совокупности по выборочной средней равна 0, 2, если известно среднее квадратическое отклонение генеральной совокупности
3. По данным 16 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений
2.4. Статистические гипотезы. Проверка гипотез Статической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Нулевой (основной) называют выдвинутую гипотезу Н0. Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит основной. Простой называют гипотезу, содержащую только одно предположение. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. В итоге проверки могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута неправильная гипотеза. Вероятность ошибки первого рода называют уровнем значимости и обозначают через Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность ошибки второго рода обозначают через Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки гипотезы. Наблюдаемым (эмпирическим) значением Кнаб называют то значение критерия, которое вычислено по выборкам. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых нулевую гипотезу принимают. Основной принцип проверки статистических гипотез: · если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; · если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают. Критическими точками (границами) Ккр называют точки, отделяющие критическую область от области принятия гипотезы. Правосторонней называют критическую область, определяемую неравенством
Левосторонней называют критическую область, определяемую неравенством
 
Двусторонней называют критическую область, определяемую неравенством В частности, если критическая область симметрична относительно нуля, то двусторонняя критическая область (в предположении, что
Мощностью критерия называют вероятность показания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Иначе мощность критерия есть вероятность того, что нулевая гипотеза отвергнута, если верна конкурирующая гипотеза. Для определения критической области задаются уровнем значимости а) для правосторонней критической области:
б) для левосторонней области:
в) для двусторонней симметричной области:
2.4.1. Сравнение двух дисперсий нормальных генеральных совокупностей По независимым выборкам, объемы которых n1 и n2, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии Правило 1. Для того чтобы при заданном уровне значимости
И по таблице критических точек распределения Фишера–Снедекора, по заданному уровню значимости Пример 2.12. По двум независимым выборкам, объем которых Решение: 1. Найдем отношение большей исправленной дисперсии к меньшей:
По условию конкурирующая гипотеза имеет вид 2. По таблице критических значений (приложение 7.), по уровню значимости 3. Так как
Задания для самостоятельной работы: 1. По двум независимым выборкам, объемы которых 2. По двум независимым выборкам, объемы которых Указание: 2.4.2. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона Эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот:
Требуется, используя критерий Пирсона, проверить гипотезу о том, что генеральная совокупность Х распределена нормально. Правило. Для того чтобы при заданном уровне значимости 1. Вычислить непосредственно (при малом числе наблюдений), или упрощенным методом (при большом числе наблюдений), например, методом произведений или сумм, выборочную среднюю 2. Вычислить теоретические частоты:
где
3. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого: 1) составляют расчетную таблицу, по которой находят наблюдаемое значение критерия 2) по таблице критических точек распределения Если Если Пример 2.13. Используя критерий Пирсона, при уровне значимости 0, 05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объема
Решение: 1. Используя метод произведений, найдем выборочную среднюю
Проверка:
Расчетные формулы:
2. Вычисляем теоретические частоты, учитывая Составим расчетную таблицу (значения функции
3. Сравним эмпирические и теоретические частоты: а) расчет сведем в таблицу и определим наблюдаемые значения критерия:
Из таблицы наблюдаемое значение критерия б) по таблице критических точек распределение
Получим Задания для самостоятельной работы: 1. Используя критерий Пирсона, при уровне значимости
2. Используя критерий Пирсона, при уровне значимости а)
б)
в)
2.5. Элементы линейной корреляции
|

 ,
, – групповая средняя группы j;
– групповая средняя группы j;  – объем группы j.
– объем группы j. ,
, – объем всей совокупности
– объем всей совокупности
 – общая средняя;
– общая средняя;  – объем всей совокупности.
– объем всей совокупности. ,
, ;
;  .
. ;
; 

 ;
;  ;
; 
 ;
; 
 и
и  , определим искомую межгрупповую дисперсию:
, определим искомую межгрупповую дисперсию:
 ;
;
 ;
; 
 определяет параметр
определяет параметр  , тем меньше будет абсолютная величина разности
, тем меньше будет абсолютная величина разности  ,
,  – оценка отклонения, чем меньше
– оценка отклонения, чем меньше  , тем точнее оценка.
, тем точнее оценка.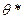 удовлетворяет неравенству
удовлетворяет неравенству  , с которой это неравенство осуществляется.
, с которой это неравенство осуществляется.
 или
или 
 .
. , который покрывает неизвестный параметр с заданной надежностью
, который покрывает неизвестный параметр с заданной надежностью  :
: ;
;  ;
;  - для нормального распределения случайной величины.
- для нормального распределения случайной величины. , где
, где  ;
; 

 , по таблице функции Лапласа (Приложение 2) находят аргумент t.
, по таблице функции Лапласа (Приложение 2) находят аргумент t. . Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним
. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним  ,
, 
 по таблице определим параметр t:
по таблице определим параметр t: , тогда
, тогда 


 :
: 
 .
.

 определяют, пользуясь распределением Стьюдента, покрывающий неизвестный параметр а с надежностью
определяют, пользуясь распределением Стьюдента, покрывающий неизвестный параметр а с надежностью  .
. и исправленное среднее квадратическое отклонение
и исправленное среднее квадратическое отклонение  . Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0.95.
. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0.95. .
.

 .
. , объем выборки n и выборочная средняя
, объем выборки n и выборочная средняя 







 .
.


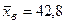 и «исправленное» среднее квадратическое отклонение
и «исправленное» среднее квадратическое отклонение  . Оценить истинное значение измеряемой величины с надёжностью
. Оценить истинное значение измеряемой величины с надёжностью 

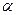 .
. .
. , где
, где  :
: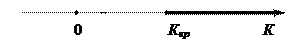

 , где
, где  :
: ,
,  , где
, где  .
. ,
,  =>
=> 




 .
. . Требуется сравнить эти дисперсии.
. Требуется сравнить эти дисперсии. о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе
о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе  , надо вычислить наблюдаемые значения критерия (отклонение большей исправленной дисперсии к меньшей):
, надо вычислить наблюдаемые значения критерия (отклонение большей исправленной дисперсии к меньшей): .
. , найти критическую точку
, найти критическую точку  (критическое значение критерия). Если
(критическое значение критерия). Если  , - нет оснований отвергнуть нулевую гипотезу. Если
, - нет оснований отвергнуть нулевую гипотезу. Если  , - нулевую гипотезу отвергают.
, - нулевую гипотезу отвергают.
 , извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии
, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии  . При уровне значимости
. При уровне значимости  проверить нулевую гипотезу
проверить нулевую гипотезу  о равенстве генеральных дисперсий, при конкурирующей гипотезе
о равенстве генеральных дисперсий, при конкурирующей гипотезе 
 , поэтому выбираем правую критическую область.
, поэтому выбираем правую критическую область. находим
находим  .
. , - нет оснований отвергнуть нулевую гипотезу. Иначе выборочные исправленные дисперсии различаются незначимо.
, - нет оснований отвергнуть нулевую гипотезу. Иначе выборочные исправленные дисперсии различаются незначимо.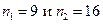 , извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии
, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии  . При уровне значимости
. При уровне значимости  проверить нулевую гипотезу
проверить нулевую гипотезу  о равенстве генеральных дисперсий при конкурирующей гипотезе
о равенстве генеральных дисперсий при конкурирующей гипотезе  .
. , извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные дисперсии
, извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные дисперсии  . При уровне значимости
. При уровне значимости  проверить нулевую гипотезу
проверить нулевую гипотезу  о равенстве генеральных дисперсий при конкурирующей гипотезе
о равенстве генеральных дисперсий при конкурирующей гипотезе  .
. ;
;  .
. и выборочное среднее квадратичное
и выборочное среднее квадратичное  .
. ,
, - объем выборки
- объем выборки  ,
,  - шаг
- шаг 
 ;
; 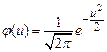 .
. ;
; , по заданному уровню значимости
, по заданному уровню значимости  (
( - число групп выборки) находят критическую точку
- число групп выборки) находят критическую точку  правосторонней критической области.
правосторонней критической области. , - нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо.
, - нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо. , - гипотезу отвергают, следовательно, эмпирические и теоретические частоты различаются значимо.
, - гипотезу отвергают, следовательно, эмпирические и теоретические частоты различаются значимо. :
: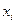






 .
. ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
;  ;
; ;
;  , т.о.
, т.о.  ;
;  .
. , по формуле
, по формуле 
 берем из приложения 1.):
берем из приложения 1.):



 .
.




 ;
; и числу степеней свободы
и числу степеней свободы  находим критическую точку (критическое значение критерия) правосторонней критической области:
находим критическую точку (критическое значение критерия) правосторонней критической области: .
. - гипотезу о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические частоты отличаются значимо.
- гипотезу о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические частоты отличаются значимо. :
:


