Параметрические колебания. Параметрический резонансПараметрические колебания – это колебания, происходящие в системе за счет периодического изменения тех параметров системы, которые определяют величину запасенной колебательной энергии. Так, например, можно возбудить параметрические колебания в колебательном контуре за счет периодического изменения электроемкости конденсатора или индуктивности катушки, параметрические колебания маятника за счет изменения длины его нити или массы груза. Если обозначить через
При таких значениях частоты Поясним это на примере периодического изменения электроемкости конденсатора колебательного контура. Пусть момент времени Таким образом, за один период колебаний в контур два раза подводится энергия. Аналогичные процессы протекают при периодическом изменении индуктивности катушки контура. Возникновение параметрических колебаний возможно и при отсутствии энергии колебаний в системе, это объясняется следующим образом. В любой колебательной системе вследствие воздействия на нее различных случайных факторов всегда существуют малые отклонения различных физических величин от их средних значений (их называют флуктуациями). Спектр частот таких флуктуаций будет непрерывным с малыми амплитудами отдельных гармоник (для напряжения на конденсаторе или индуктивности они составляют значения порядка микровольта). Периодическое изменение параметра системы на частоте, кратной Такое возбуждение колебаний в системе получило название параметрического резонанса. Нарастание амплитуды колебаний при параметрическом резонансе ограничивается при достаточно больших амплитудах нелинейными эффектами. К ним можно отнести, например, возникновение зависимости активного сопротивления R от амплитуды силы тока в контуре (это приводит к увеличению потерь энергии на выделение джоулевой теплоты) или зависимости электроемкости конденсатора от напряжения (это приводит к изменению частоты Явление параметрического резонанса используется при работе малошумящих параметрических усилителей СВЧ-диапазона, в которых применяются параметрические полупроводниковые диоды с управляемой емкостью р-n перехода. Примером параметрического резонанса в механической системе является маятник в виде груза массы m, подвешенного на нити, длину
Раскачка качелей также обусловлена параметричес- ким резонансом, когда эффективная длина маятника (положение центра тяжести) изменяется при приседаниях и вставаниях человека. Рис. 5.26
|

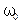 частоту собственных незатухающих колебаний в системе, то параметрическое возбуждение колебаний в системе наступает в тех случаях, когда частота периодического изменения
частоту собственных незатухающих колебаний в системе, то параметрическое возбуждение колебаний в системе наступает в тех случаях, когда частота периодического изменения  параметра системы будет удовлетворять условию
параметра системы будет удовлетворять условию . (5.91)
. (5.91) , так как на этой частоте совершает колебания энергия системы (потенциальная и кинетическая энергии, энергия электрического поля конденсатора и магнитного поля катушки индуктивности). При такой частоте колебания в системе будут наиболее интенсивными.
, так как на этой частоте совершает колебания энергия системы (потенциальная и кинетическая энергии, энергия электрического поля конденсатора и магнитного поля катушки индуктивности). При такой частоте колебания в системе будут наиболее интенсивными. , заряд на обкладках конденсатора будет максимальным и в этот момент времени скачком (за время, малое по сравнению с периодом собственных колебаний) раздвигаются пластины конденсатора. Тогда энергия электрического поля конденсатора будет увеличиваться, в контур поступает энергия:
, заряд на обкладках конденсатора будет максимальным и в этот момент времени скачком (за время, малое по сравнению с периодом собственных колебаний) раздвигаются пластины конденсатора. Тогда энергия электрического поля конденсатора будет увеличиваться, в контур поступает энергия:  . Через четверть периода колебаний (
. Через четверть периода колебаний (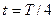 ) конденсатор будет разряжен (
) конденсатор будет разряжен ( ), вся энергия контура будет сосредоточена в катушке в виде энергии магнитного поля. Поэтому сближение обкладок конденсатора в этот момент времени не приводит к отводу энергии колебаний из контура.
), вся энергия контура будет сосредоточена в катушке в виде энергии магнитного поля. Поэтому сближение обкладок конденсатора в этот момент времени не приводит к отводу энергии колебаний из контура.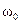 собственных колебаний и в результате к увеличению расстройки (
собственных колебаний и в результате к увеличению расстройки (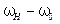 ) между частотами
) между частотами  которой можно изменять (рис. 5.26, а).
которой можно изменять (рис. 5.26, а). Если уменьшать длину в нижнем положении и увеличивать в крайних положениях, то работа внешней силы за один период колебаний будет положительной и амплитуда колебаний будет возрастать. Траектория движения груза при таких колебаниях показана на рис. 5.26, б
Если уменьшать длину в нижнем положении и увеличивать в крайних положениях, то работа внешней силы за один период колебаний будет положительной и амплитуда колебаний будет возрастать. Траектория движения груза при таких колебаниях показана на рис. 5.26, б


