Вектор Умова

Упругая волна, распространяясь в среде, несет с собой энергию от источника колебаний, что приводит к появлению в среде дополнительной энергии, связанной с колебаниями частиц среды – это и есть энергия волны. Запишем для нее формулу. Для этого рассмотрим плоскую продольную гармоническую волну (6.3), распространяющуюся в положительном направлении оси .

Для малого объема среды (он представляет собой цилиндр площади основания и высоты , рис. 6.6, а) скорости всех частиц будут одинаковы

,

и поэтому кинетическая энергия частиц в этом объеме, связанная с их колебаниями около своих положений равновесия, будет равна

, (6.10)

где введена плотность среды, позволяющая выразить массу m всех частиц в объеме V.

Величина деформации этого малого объема будет равна , а относительная деформация в виду малости объема () (см. рис. 6.6, а) будет равна . Потенциальную энергию W_Р такого деформированного объема можно оценить по формуле: , где представляет коэффициент жесткости среды.

Рис. 6.6

 

Обычно упругие свойства твердого тела определяют модулем Е Юнга, который характеризует сопротивляемость материала упругой твердой среды деформациям сжатия или растяжения. Поэтому выразим потенциальную энергию через модуль Е Юнга. Для этого на основе двух выражений закона Гука запишем формулу связи между коэффициентом жесткости и модулем Юнга:

, (6.11)

где величина называется механическим напряжением, а –относительным удлинением.

Тогда для потенциальной энергии W_Р деформированного объема можно записать

. (6.12)

В случае жидких и газообразных сред вместо модуля Е Юнга нужно в формулу (6.12) подставить модуль k объемной упругости газа или жидкости, который характеризует способность газа или жидкости сопротивляться изменению их объема.

Из теории колебаний известно, что максимальные значения кинетической и потенциальной энергий при ГК совпадают: , и поэтому

. (6.13)

Следовательно, полную энергию волны в объеме V можно представить в следующем виде:

. (6.14)

Эта формула позволяет ввести объемную плотность энергии волны

, (6.15)

где учтено, что рассматриваемый объем V является малым.

Из формулы (6.15) следует, что объемная плотность энергии бегущей волны зависит от координат и времени по гармоническому закону, т.е. представляет собой бегущую волну энергии колебаний в среде, следовательно, в среде происходит перенос энергии источника колебаний.

Полученные выражения справедливы и для поперечной волны, которая распространяется только в твердых телах. В этом случае вместо модуля Юнга необходимо записывать в формулах модуль сдвига G.

Введем энергетические характеристики, описывающие перенос энергии волнового процесса в среде.

1. Мощность излучения источника колебаний – это энергия, излучаемая источником колебаний за единицу времени

. (6.16)

2. Поток энергии через какую-либо поверхность – это энергия, переносимая через какую-либо поверхность за единицу времени (рис. 6.6, б)

. (6.17)

Из формулы (6.17) следует, что мощность излучения источника равна потоку энергии через замкнутую поверхность, окружающую источник колебаний: (рис. 6.6, в).

3. Вектор Умова или вектор плотности потока энергии – это вектор, направление которого совпадает с направлением скорости волны, а его модуль равен энергии, переносимой за единицу времени, через единичную площадку , расположенную перпендикулярно направлению переноса энергии (рис.6.6, г):

. (6.18)

Для модуля вектора Умова можно получить следующую формулу

,

где введена объемная плотность энергии волны в среде. Тогда для вектора Умова можно записать

. (6.19)

4. Интенсивность упругой волны I равна усредненному по времени значению модуля вектора Умова

.(6.20)

Введение интенсивности связано с тем, что многие приборы при достаточно высокой циклической частоте 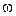волны измеряют не мгновенное, а усредненное по времени значение модуля вектора Умова.