Электр техникалық қондырғылардағы жылу тасымалдағыштың негізгі теориялары
Жылу тасымалдағ ыш – жылу таралу ү рдістерін қ арастыратын ғ ылым. Жылу тасымалдаудың негізгі ү ш тү рі бар: жылу ө ткізгіштік, конвекция жә не сә улелену. Жылу ө ткізгіштік – денелер бір біріне немесе дененің бір бө лігінен басқ асына жылу энергиясының тікелей тасымалдануы. Жылу ө ткізгіштік таза тү рдегі монолитті қ атты денелердің ішіндегі немесе газ, сұ йық қ озғ алмайтын жұ қ а қ абаттарда жылу тасымалы кезінде байқ алады. Конвекция – зат (кө леммен) бө лшектерінің ауысу есебінен пайда болғ ан жылу энергиясының тасымалы. Конвекция тек қ озғ алмалы – сұ йық тық немесе газдық ортада айқ ын орын алады. Конвекция ә рқ ашан да сұ йық тың немесе газдың жің ішке қ абаттарындағ ы жылу тасымалымен жү реді. Сә улелену – жылу энергияларының электр магниттік толқ ын тү ріндегі таралуынан болады. Бұ л ү рдіс жылу сә улелері ү шін мө лдір орталарда жә не жылу алмасуғ а қ атысып жатқ ан денелердің энергиясының ауысуымен жү реді, сә улеленген дененің жылу энергиясының бір бө лігі электр магнитте, ал кері ауысу жұ татын дене бетінде болады. Вакуумдағ ы жылу тасымалы тек сә улеленумен жү реді. Жылу таралу ү рдістерінде бір уақ ытта екі немесе ү ш жылу тасымалдағ ыш тү рі қ атысады. Жылу тасымалдау ү рдісі кең істіктегі температура, уақ ыт ө згерісіне байланысты жү реді. Дә л осы уақ ыттағ ы температураның мағ ынасы температура ө рісі деп аталады. Жалпы жағ дайда температура ө рісі мынадай математикалық ө рнекке ие болады:
Егерде дененің нү ктесіндегі температура уақ ыт бойынша ө згермесе, температура ө рісі стационарлы деп аталады. Жылу тасымалының жылу ө ткізгіштік стационарлы ү рдісі келесі жағ дайғ а ие: мысалы, футерленген – пештің қ абырғ алары ұ зақ ү здіксіз жұ мыс істегенде байқ алады. Стационарлық емес ү рдістер денені қ ыздыру мен суытуғ а тә н. Температуралық ө рістің негізгі сипаттаушысы температура градиенті – вектор, температурадан норма бойынша изотермиялық жазық тық қ а қ атынасына тең шама:
мұ ндағ ы
Жылу ө ткізгіштікпен жылу тасымалдау. Кө птеген материалдар ү шін ө ткізгіштік коэффицентінің температурағ а тә уелділігі келесі тү де кө рсетіледі:
мұ ндағ ы
Таза металлдар ү шін температура артқ анда жылу ө ткізгіштік коэффициент азаяды (дә л меншікті электр ө кізгіштік сияқ ты), ал балқ ымалар мен қ ұ рылыс, ө ртке қ арсы жә не жылу оқ шауланғ ан материалдарында азаяды. Стационарлы режимдегі жылу ө ткізгіштік. Жобаланып жатқ ан пеш қ абырғ алары арқ ылы жоғ алатын жылуды есептеу ү шін қ абырғ а шегі мен сә улелену жылу алмасуы жә не қ абырғ а арқ ылы жылу тасымалдануының жылу ө ткізгіштігін ескеретін формулалар қ олданылады (3.1-сурет).
3.1-сурет. Кө п қ абатты қ абырғ а арқ ылы жылу тасымалдану сұ лбасы
Кө п қ абатты қ абырғ а тегіс қ абырғ а арқ ылы ө тетін жылу ағ ымының ақ ырғ ы ө лшеміне тең:
мұ ндағ ы
Жылу беру коэффициенті қ абырғ а шегінде жылулмасудың сипаттамасы болып табылады:
мұ ндағ ы ак - конвекцияның жылу беруін есептесе, ас - жылудың сә улеленуін ескереді.
Жылу беру коэффициентінің мә ні алдымен жылу алмасуғ а қ атысушы дене мен ортаның физикалық қ асиеті, температурағ а тә уелді. Кірпіш немесе металл қ абырғ ада температурасы 10 немесе 20°С қ алыпты ауа арасында жылу алмасу болса, онда жылу берудің қ осынды коэффициенті қ абырғ а температурасына тә уелді ө згереді (3.1-кесте)
3.1-кесте.
Қ абырғ аның ішкі бетімен і жә не і+1 қ абаттың арасындағ ы температура:
Жұ мысшы температурасы Берілген температуралы орталардағ ы кө п қ абатты цилиндр қ абырғ асы (п қ абат) арқ ылы ө тетін жылу легі қ абырғ аның сыртқ ы жә не ішкі беттерінде (1м ұ зындық ү шін) тең:
мұ ндағ ы
Цилиндр қ абырғ асының ішкі бетімен і жә не (і +1)қ абаттар арасындағ ы температура:
(3.8)
Кө п қ абатты шарлы қ абырғ адан ө тетін жылу шегі:
Шарлы қ абырғ аның ішкі бет шегінде мен і жә не (і+1) қ абаттар арасындағ ы температуралар:
Стационарлы емес режимдегі жылу ө ткізгіштік. Денені қ ыздыру мен суыту. x, y, z координатасына жә не
3.2-сурет. Шектің шарттары бойынша беттің температура ү рдісінің барлық уақ ытының
мұ ндағ ы
Дене қ абатының беттік температура градиенті:
tнав=const бастапқ ы шарты мен t 2 = 0 =t 0, бастапқ ы шарт кезіндегі шексіз цилиндр жә не шектелмеген пластина қ ызуы мен сууы. Бұ л жағ дай сұ йық ортадағ ы сууы мен қ ыздыруды есептеу ү шін, сонымен бірге қ ыздыру мен суыту ү рдісіндегі температура тең есуін есептеу ү шін практикалық мә ні зор. Жылу ө ткізгіштік тең деуінің дифференциалдық шешуі:
tпов=const жә не t 2 = 0 =t 0болғ андағ ы қ алың дығ ы 25 шектелмеген пластина ү шін ү рдістердің физикалық ұ қ састығ ын сипаттайтын шама кешендік тү рде келтіріледі:
мұ ндағ ы
3.3-суретте Ө температура қ атыстының Фурье санына тә уелділігі кө рсетілген.
3.3-сурет. Ө температура қ атыстының Фурье санына тә уелділігі Радиусы R ұ зындық ты шексіз цилиндр жылу ө ткізгіштік тең деуінің дифференциалдық шешуі ұ қ састық тең деуі келесі тү рде кө рсетілген:
мұ ндағ ы
Бастапқ ы шарт ретінде қ иылысу бойынша параболаның таралуы ү лкен орынғ а ие. Пластина ү шін:
цилиндр ү шін:
Пластина беті x=s, пластина центрі x= 0 жә не Ұ қ састық тең деу формасындағ ы шешімі: шектелмеген пластина –
цилиндрдің шексіз ұ зындығ ы ү шін –
Шектік шарты qn=const жә не бастапқ ы шарт t Ұ қ састық саны кезіндегі шектелмеген пластина ү шін жылу ө ткізгіштік тең деуінің дифференциалдық тең деуі:
Бұ л шешіммен берілген меншікті жылу шегін қ абылдайтын пластина бетінің x/s ә ртү рлі мә ндеріндегі пластина қ иылысуының ә р тү рлі нү ктелеріндегі берілген температурағ а дейін қ ызуын (сууын) немесе ү рдіс басталғ аннан кейінгі соң ғ ы Ұ қ састық санындағ ы шексіз ұ зындық ты цилиндр ү шін жылу ө ткізгіштіктің дифференциалдық тең деу шешімі:
Бастапқ ы шарты t 25 мм қ алың дық ты шектелмеген пластина ү шін жылу ө ткізгіштіктің дифференциалдық тең деу шешімі.
3.4-сурет. Беттегі qn жылу шекті тұ рақ ты тығ ыздық кезіндегі қ атыстық радиусы
Қ оршағ ан ортаның (tокр=const) температура тұ рақ тылығ ы ұ қ састық сан тү рінде келесі тү рде кө рсетіледі:
(x/s=l) бетті жә не (x/s - 0) центрлі пластинаның тә уелділігі келтірілген (3.5-сурет). Сол арқ ылы беттің қ ызу (суу) уақ ытын жә не пластина ортасының берілген температурасын, х уақ ыттан кейінгі осы нү ктелердегі температурасын анық тауғ а болады. R радиусты шексіз ұ зындық ты цилиндр ү шін жылу ө ткізгіштік тең деуінің шешімі ұ қ састық саны бойынша:
(r / R-l) бет пен (r / R= 0) осьті цилиндрдің тә уелділігі берілген. x/s= 0, 2; 0, 4; 0, 6 жә не 0, 8 - пластина ү шін. r / R =0, 2; 0, 4; 0, 6; 0, 8 - цилиндр ү шін шешімдер келтірілген.
Конвективті жылу алмасу. Конвективті жылу алмасу Ньютон формуласымен ө рнектеледі:
3.5-сурет. Беттегі
мұ ндағ ы Qк – конвекция мен берілетін жылу шегі; Fк – конвективті жылу алмасу бетінің ауданы; tср – газ немесе сұ йық тың орташа температурасы; tст – қ абырғ аның температурасы; aк - конвекция жылу беру коэффициенті.
Конвекция еркін (табиғ и) жә не еріксіз (жасанды) конвекция болып бө лінеді. Ортаның ось бойынша қ озғ алысы ә р тү рлі тығ ыздық та, яғ ни ортаның біртекті емес температуралық ө рісімен белгіленіп, туындалады; еріксіз қ озғ алысқ а сорғ ы, желдеткіш т.с.с. негізделіп жасалынады. Ортаның қ озғ алысы ә лсіз жылдамдық пен ламинарлы сипатта болады (ө зара араласпайтын параллель ағ ыстар), бұ л жерде ерекше рө лге ортаның жылу ө ткізгіштігі ие. Ү лкен жылдамдық та қ озғ алыс қ ұ йын тү рінде болады да, турбалентті деп аталады, мұ ндай режимде қ абырғ а жанында қ алың дығ ы азайғ ан сайын қ озғ алыс жылдамдығ ы артатын ламинарлы қ абат сақ талады. Конвективті жылу алмасу жылу ө ткізгіштік, қ озғ алыс бір тегістік жә не бір мә нділік шарттар тең деу жү йесімен сипатталады. Мұ ндай тең деулердің аналитикалық шешімі ү лкен қ иындық тар туғ ызады, сондық тан конвективті жылу алмасу тә жірибелік нә тижеге негізделген. Конвективті жылу беру коэффициентінің мә нін анық тайтын ұ қ састық тең деуінің тү рі:
Nu=f (Gr; Pe; Re). (3.25)
Нульссельт Грасгоф санына Пекие санына Pe=wL/aорт кіреді: ортаның қ озғ алыс жылдамдығ ы w, aорт жылу ө ткізгіштік коэффициенті. Пекие саны келесі тү рде келтірілуі мү мкін:
Рейнольдс саны Re=w/jv процесінің гидродинамикасын ө рнектейді. Прандтл саны Pr=V/а ортаның физикалық қ асиетін ө рнектейді. Онда (3.25) формула келесі тү рде болады:
Nu = f(Gr; Pr; Re). (3.27)
Ерікті конвекция кезінде Nu:
Nu = f(Gr; Pr). (3.28)
Pr=idem кезіндегі газдар ү шін бірдей атомдық (ә сіресе ауа ү шін) Nu=f (Gr)тү ріне келеді. Кө птеген газ ү шін Прандтл саны қ ысым мен температура ө згеруімен аз ө згереді. Еріксіз конвекция мен турбалентті режимде Nu келесі тү рде болады:
Nu = f (Re; Pr), (3.29)
Бірдей атом санды газ ү шін Nu келесі тү рде болады:
Nu = f (Re). (3.30)
Қ оршағ ан ортаның температурасы тұ рақ ты болғ анды Фурье мен Био санына шексіз ұ зындық ты цилиндр осінің қ атысты температура тә уелділігі 3.6-суретте келтірілген.
3.6-сурет. Қ оршағ ан ортаның температурасы тұ рақ ты болғ анды Фурье мен Био санына шексіз ұ зындық ты цилиндр осінің қ атысты температура тә уелділігі
Табиғ и конвекция кезіндегі жылу алмасу. Ұ қ састық сандарын ө ң деу кезінде ү лкен сан – тә жірибесі қ атты денеден сұ йық немесе газ тә різді ортада бос ағ ып ө ткендегі жылу беру коэффициентінің орташа мә нін анық тайтын тә уелділіктен алынады. 103 < (Gr Pr) орт < 109 диапазон мә ніндегі ламинарлы режимдегі оның қ озғ алысындағ ы кез келген ағ ысты орта мен беттің, жазық тық немесе вертикальды цилиндрлі дененің жылу алмасуы ү шін:
Nucp =0, 76(GrPr) cр 0.25(Prcp / PrC T)0.25. (3.31)
(GrPr) орт > 109 кезіндегі турбулентті режим қ озғ алысы ү шін:
Nucp = 0, 15(GrPr) cр 0.38 (Prcp / PrCT)0.25. (3.32)
Мұ нда ө лшемін анық таушы ретінде жазық тық тың h биіктігі алынады, орта параметрінің физикалық параметрімен таң далып, анық тауыш температура ретінде Grорт мен Prорт мә ндер есептеліп, tорт қ абырғ адан қ ашық орта температурасы алынады. Формуладағ ы (Prорт / Prқ аб)0, 25 параметрінде жылу беру бағ ыты (қ атты денеден ортағ а немесе кері) жә не орта мен қ абырғ а арасындағ ы температуралық ауысуы (газ ү шін Prорт/ Prорт =1)ескеріледі. Ортаның еркін қ озғ алысы шартындағ ы кө лденең қ ұ быр (стержень, прут, сым) жылу беру кезіндегі тә уелділік тү рі:
Nucp = 0, 5(GrPr)cр0.25 (Prcp/PrCT)0.25. (3.33)
Анық тау ө лшем ретінде мұ нда қ ұ быр диаметрі d алынады. Бекітілген кө лем ішіндегі жылу алмасу қ абаттары сұ йық немесе газбен толтырылғ анда қ абырғ а температурасы ә р тү рлі мә нде ортаның циркуляциясы туындайды. Жылу алмасу қ абаттары ең жақ сы қ ызғ ан қ абырғ адан жылу берілу ортаның қ асиетіне, температурасына, қ абырғ а температурасының айырмашылығ ына, бекітілген кө лемнің формасы мен ө лшеміне, сонымен бірге салқ ын жә не ыстық қ абырғ аның ө зара орналасуына тә уелді. Қ абаттардағ ы конвекция кезіндегі жылу шегін анық таудың тә жірибелік есебінде біртекті тегіс қ абырғ а арқ ылы жылу ө ткізгіштікпен жылу беруді ө рнектейтін формула қ олданылады:
мұ ндағ ы
eK = f (GrPr) cp. (3.35)
Ортаның температурасы:
(GrPr) ср < 103
103< (GrPr)cp< 106 кезінде ЕК = 0, 105 (GrPr)ср0.3. (3.37)
10e< (GrPr)cp< 1010 кезінде eK = 0, 4(GrPr)o.2cp (3.38)
Барлық мә ндер ү шін жуық тау GrPr > 103 деп қ абылдауғ а болады:
Формулалар кез келген тегіс, кө лденең, тік, сақ ина, сфералық жә не т.б. форма тү ріндегі қ абаттар қ олданылады. Грасгоф санын есептеу кезінде анық тауыш ө лшем ретінде қ абат қ алың дығ ы Snp қ абылданады. Ортаның еріксіз қ озғ алысы кезіндегі жылу алмасу. Қ атты дененің конфигурациясы, жылдамдығ ы, қ озғ алыс сипаты мен ортаның физикалық қ асиетіне байланысты ортаның еріксіз қ озғ алысы кезіндегі жылудың ұ қ састық тең деуі де ә р тү рлі. Тө менде кейбір еріксіз конвекция жағ дайлары ү шін есептеу формулалары келтірілген. Ортаның ламинарлы шегі (Reср Пластина:
Prcp> > 0, 5 кезінде Nucp= 0, 67 Prcp //2 Recp //2, (3.39) Drcp< < 1 (сұ йық металл) кезінде
Дө ң гелек тік
PecpD/
Рecpб /1> 70 кезіндегі ұ зындығ ы 1 жә не ені б тегіс саң ылау.
Рecpб /1
кезінде (сұ йық металл) немесе Nucp = 3, 3 + 0, 14Pe0.8.
Nucp = 3, 3 + 0, 14Pe0.8. анық таушы ө лшемі б1= D2 (3.44)
|

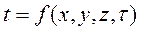 . (3.1)
. (3.1)
 (3.2)
(3.2) – бірлік вектор, нормаль бойынша изотермиялық жазық тық қ а бағ ытталғ ан.
– бірлік вектор, нормаль бойынша изотермиялық жазық тық қ а бағ ытталғ ан. ; (3.3)
; (3.3) -дегі жылу ө ткізгіштік коэффициенті,
-дегі жылу ө ткізгіштік коэффициенті,  – жылу ө ткізгіштік коэффициентінің температуралық коэффициенті.
– жылу ө ткізгіштік коэффициентінің температуралық коэффициенті.
 , (3.4)
, (3.4) мен
мен  – ішкі жә не сыртқ ы бетпен ө тетін температура ортасы;
– ішкі жә не сыртқ ы бетпен ө тетін температура ортасы; 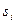 – қ абырғ аның 1–қ абаттың қ алың дығ ы;
– қ абырғ аның 1–қ абаттың қ алың дығ ы; 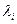 – қ абырғ аның 1–қ абаттың материалының жылу ө кізгіштік коэффициенті;
– қ абырғ аның 1–қ абаттың материалының жылу ө кізгіштік коэффициенті;  – 1–қ абат бетінің есептік ауданы, мысалы і -ші қ абат ү шін
– 1–қ абат бетінің есептік ауданы, мысалы і -ші қ абат ү шін  , егер де
, егер де  жә не
жә не  болғ анда сә йкесінше басқ а қ абат беттерінің есептік ауданы анық талады;
болғ анда сә йкесінше басқ а қ абат беттерінің есептік ауданы анық талады;  жә не
жә не 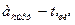 - температуралы ортадан қ абырғ аның ішкі бетіне жә не
- температуралы ортадан қ абырғ аның ішкі бетіне жә не  температуралы ортағ а сыртқ ы қ абырғ адан жылу беру коэффициенті.
температуралы ортағ а сыртқ ы қ абырғ адан жылу беру коэффициенті.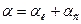 , (3.5)
, (3.5) жылу беруінің қ осынды коэффициенті, Вт/ (м² °С)
жылу беруінің қ осынды коэффициенті, Вт/ (м² °С)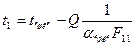
 . (3.6)
. (3.6) °C-ге тең кездегі пеш қ абырғ аларында жоғ алғ ан жылуды есептеу кезінде
°C-ге тең кездегі пеш қ абырғ аларында жоғ алғ ан жылуды есептеу кезінде  мә нін есептемеуге болады, себебі мұ ндағ ы жылу беру коэффициенті тым ү лкен, бұ л жағ дайда
мә нін есептемеуге болады, себебі мұ ндағ ы жылу беру коэффициенті тым ү лкен, бұ л жағ дайда  ауыстыру керек.
ауыстыру керек. , (3.7)
, (3.7) мен
мен  – і -ші қ абатты шектейтін беттер диаметрі.
– і -ші қ абатты шектейтін беттер диаметрі. кезінде тегіс қ абырғ алар ү шін қ абат қ алың дығ ы
кезінде тегіс қ абырғ алар ү шін қ абат қ алың дығ ы  формуланы қ олдануғ а болады, ал беттің есептік аудан мә ндері – қ абат бетінің сыртқ ы жә не ішкі аудандарының арифметикалық ортасы.
формуланы қ олдануғ а болады, ал беттің есептік аудан мә ндері – қ абат бетінің сыртқ ы жә не ішкі аудандарының арифметикалық ортасы. ,
, .
. . (3.9)
. (3.9)
 . (3.10)
. (3.10) уақ ытқ а тә уелді денедегі температураның таралу заң дылығ ын анық таудың шешуі бір мә нділік (қ исық тар шарты) шартымен бірге жылу ө ткізгіштің дифференциалдық тең деуіне сә йкес келеді. Жылу ө ткізгіштің тең деу шешімі қ арапайым бір ө лшемді температура ө рісі бар жағ дайлар шексіз ұ зын цилиндр мен шексіз пластиналар ү шін берілген, берілген тапсырмада дененің белгілі физикалық параметрлері, геометриялық параметрлері (пластина қ алың дығ ы 25), шектік шарт пен
уақ ытқ а тә уелді денедегі температураның таралу заң дылығ ын анық таудың шешуі бір мә нділік (қ исық тар шарты) шартымен бірге жылу ө ткізгіштің дифференциалдық тең деуіне сә йкес келеді. Жылу ө ткізгіштің тең деу шешімі қ арапайым бір ө лшемді температура ө рісі бар жағ дайлар шексіз ұ зын цилиндр мен шексіз пластиналар ү шін берілген, берілген тапсырмада дененің белгілі физикалық параметрлері, геометриялық параметрлері (пластина қ алың дығ ы 25), шектік шарт пен  бастапқ ы шарты, дененің қ оршағ ан ортамен жылу алмасуы сипатталатын бір мә нді шарттар тү рі келтірілген. 3.2-суретте шектің шарттары бойынша беттің температура ү рдісінің барлық уақ ытының
бастапқ ы шарты, дененің қ оршағ ан ортамен жылу алмасуы сипатталатын бір мә нді шарттар тү рі келтірілген. 3.2-суретте шектің шарттары бойынша беттің температура ү рдісінің барлық уақ ытының  жылу ағ ымы немесе орта мен беттің арасындағ ы жылу алмасу заң ы мен қ оршағ ан температурасы
жылу ағ ымы немесе орта мен беттің арасындағ ы жылу алмасу заң ы мен қ оршағ ан температурасы  кө рсетілген.
кө рсетілген.
 жылу ағ ымы немесе орта мен беттің арасындағ ы жылу алмасу заң ы мен қ оршағ ан температурасы
жылу ағ ымы немесе орта мен беттің арасындағ ы жылу алмасу заң ы мен қ оршағ ан температурасы 
 , (3.11)
, (3.11) - қ оршағ ан температурасы,
- қ оршағ ан температурасы,  - жылу ағ ымы немесе орта мен беттің арасындағ ы жылу температурасы.
- жылу ағ ымы немесе орта мен беттің арасындағ ы жылу температурасы. . (3.12)
. (3.12) , (3.13)
, (3.13) , (3.14)
, (3.14) 2=P0 – Фурье саны (пластиналар ү шін); x/s - қ атысты координатасы, a-
2=P0 – Фурье саны (пластиналар ү шін); x/s - қ атысты координатасы, a-  - температура ө ткізгіштіктік коэффициенті; s – меншікті жылу сыйымдылық; y – тығ ыздық.
- температура ө ткізгіштіктік коэффициенті; s – меншікті жылу сыйымдылық; y – тығ ыздық.
 , (3.15)
, (3.15) /R2= P0 – Фурье саны (цилиндр ү шін)
/R2= P0 – Фурье саны (цилиндр ү шін) 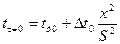 , (3.16)
, (3.16) . (3.17)
. (3.17) t0=tпов – tцо ү шін -
t0=tпов – tцо ү шін -  бастапқ ы сә ттегі пластинаның центрі мен беті арасындағ ы температура берілуі.
бастапқ ы сә ттегі пластинаның центрі мен беті арасындағ ы температура берілуі. , (3.18)
, (3.18) . (3.19)
. (3.19) . (3.20)
. (3.20) . (3.21)
. (3.21) 0 жә не tокр=const шектік шартты шексіз ұ зын цилиндр мен шектелмеген пластина қ ызуы мен сууы.
0 жә не tокр=const шектік шартты шексіз ұ зын цилиндр мен шектелмеген пластина қ ызуы мен сууы.
 мен Фурье санына qx/R2 шексіз ұ зындық ты цилиндр қ атыстық температурасының тә уелділігі
мен Фурье санына qx/R2 шексіз ұ зындық ты цилиндр қ атыстық температурасының тә уелділігі . (3.22)
. (3.22) - Био саны (жылу техникалық -массивінің критерийі).
- Био саны (жылу техникалық -массивінің критерийі). Fk, (3.24)
Fk, (3.24)
 жылу шекті тұ рақ ты тығ ыздығ ындағ ы
жылу шекті тұ рақ ты тығ ыздығ ындағ ы 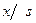 қ атыстық координатасы мен
қ атыстық координатасы мен  2 Фурье санына пластинаның қ атыстық температурадағ ы тә уелділігі
2 Фурье санына пластинаның қ атыстық температурадағ ы тә уелділігі санына кіреді: анық таулы ө лшемі l - тор ұ зындығ ы, қ ұ быр диаметрі жә не т.с.с.,
санына кіреді: анық таулы ө лшемі l - тор ұ зындығ ы, қ ұ быр диаметрі жә не т.с.с., 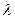 орт -ортаның жылу ө ткізгіштігі.
орт -ортаның жылу ө ткізгіштігі. 3/g
3/g  2 кіреді: ортаның кө лемдік ұ лғ аю коэффициенті
2 кіреді: ортаның кө лемдік ұ лғ аю коэффициенті  ортаның кинетикалық тұ тқ ырлығ ы
ортаның кинетикалық тұ тқ ырлығ ы  , g еркін тү су ү деуі жә не температуралық ауысу
, g еркін тү су ү деуі жә не температуралық ауысу 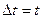 орт – tcm.
орт – tcm. . (3.26)
. (3.26)
 , (3.34)
, (3.34) – салқ ын жә не ыстық қ абырғ аның температурасы, Snp – қ абат қ алың дығ ы,
– салқ ын жә не ыстық қ абырғ аның температурасы, Snp – қ абат қ алың дығ ы,  к
к 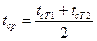 (3.36)
(3.36) )
)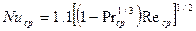
 ұ зындық ты қ ұ бырдың D диаметрі PecpD/
ұ зындық ты қ ұ бырдың D диаметрі PecpD/  (3.40)
(3.40) 12кезінде Nu= 3, 66.
12кезінде Nu= 3, 66. (3.41)
(3.41) 50, 0, 6 < Pr< 100 кезіндегі диаметрі D жә не ұ зындығ ы
50, 0, 6 < Pr< 100 кезіндегі диаметрі D жә не ұ зындығ ы  (3.42)
(3.42) (3.43)
(3.43) (3.45)
(3.45)


