I. Свойство линейности.
Если имеется некоторая совокупность сигналов  причём
причём 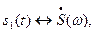
 , …, то взвешенная сумма сигналов преобразуется по Фурье следующим образом:
, …, то взвешенная сумма сигналов преобразуется по Фурье следующим образом:
 (2.11)
(2.11)
Здесь  - произвольные числовые коэффициенты.
- произвольные числовые коэффициенты.
II. Теорема о сдвигах.
Предположим, что для сигнала  известно соответствие
известно соответствие 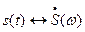 . Рассмотрим такой же сигнал, но возникающий на
. Рассмотрим такой же сигнал, но возникающий на  секунд позднее. Принимая точку
секунд позднее. Принимая точку  за новое начало отсчёта времени, обозначим этот смещённый сигнал как
за новое начало отсчёта времени, обозначим этот смещённый сигнал как  . Введём замену переменной:
. Введём замену переменной:  . Тогда
. Тогда  ,
, 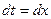
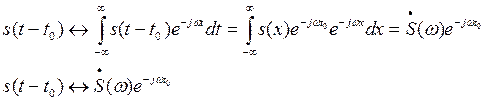
Модуль комплексного числа  при любых
при любых  равен 1, поэтому амплитуды элементарных гармонических составляющих, из которых складывается сигнал, не зависят от его положения на оси времени. Информация об этой характеристике сигнала заключена в частотой зависимости аргумента от его спектральной плотности (фазовом спектре).
равен 1, поэтому амплитуды элементарных гармонических составляющих, из которых складывается сигнал, не зависят от его положения на оси времени. Информация об этой характеристике сигнала заключена в частотой зависимости аргумента от его спектральной плотности (фазовом спектре).
III. Теорема масштабов.
Предположим, что исходный сигнал  подвергнут изменению масштаба времени. Это означает, что роль времени
подвергнут изменению масштаба времени. Это означает, что роль времени  играет новая независимая переменная
играет новая независимая переменная 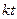 (
( - некоторое вещественное число.) Если
- некоторое вещественное число.) Если  > 1, то происходит “ сжатие” исходного сигнала; если же 0<
> 1, то происходит “ сжатие” исходного сигнала; если же 0<  < 1, то сигнал “растягивается” во времени. Если
< 1, то сигнал “растягивается” во времени. Если  , то:
, то:
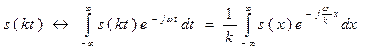
Произведём замену переменной  , тогда
, тогда  , откуда следует:
, откуда следует:
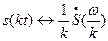 (2.13)
(2.13)
При сжатии сигнала в  раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в
раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в  раз.
раз.
Очевидно, что при растягивании сигнала во времени (т.е. при  < 1) имеет место сужение спектра и увеличение модуля спектральной плотности.
< 1) имеет место сужение спектра и увеличение модуля спектральной плотности.
IV. Теорема о спектре производной и неопределённого интеграла.
Пусть сигнал  и его спектральная плоскость
и его спектральная плоскость  заданы. Будем изучать новый сигнал
заданы. Будем изучать новый сигнал  и поставим цель найти его спектральную плотность
и поставим цель найти его спектральную плотность  .
.
По определению:
 (2.14)
(2.14)
Преобразование Фурье – линейная операция, значит, равенство (2.14) справедливо и по отношению к спектральным плотностям. Получаем по теореме о сдвигах:
 (2.15)
(2.15)
Представляя экспоненциальную функцию рядом Тейлора:  подставляя этот ряд в (2.15) и ограничиваясь первыми двумя числами, находим
подставляя этот ряд в (2.15) и ограничиваясь первыми двумя числами, находим
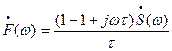
 (2.16)
(2.16)
Итак, дифференцирование сигнала по времени эквивалентно простой алгебраической операции умножения спектральной плотности на множитель  . Поэтому говорят, что мнимое число
. Поэтому говорят, что мнимое число  является оператором дифференцирования, действующим в частотной области.
является оператором дифференцирования, действующим в частотной области.
Вторая часть теоремы. Рассмотренная функция  является неопределённым интегралом по отношению к функции
является неопределённым интегралом по отношению к функции  . Интеграл это есть
. Интеграл это есть  , значит
, значит  - его спектральная плотность, а
- его спектральная плотность, а  из формулы (2.16) равна:
из формулы (2.16) равна:
 (2.17)
(2.17)
Таким образом, множитель  служит оператором интегрирования в частотной области.
служит оператором интегрирования в частотной области.
V. Теорема о свёртке.
Как известно, при суммировании сигналов их спектры складываются. Однако спектр произведения сигналов не равен произведению спектров, а выражается некоторым специальным интегральным соотношением между спектрами сомножителей.
Пусть  и
и  - два сигнала, для которых известны соответствия
- два сигнала, для которых известны соответствия  ,
,  .Образуем произведение этих сигналов:
.Образуем произведение этих сигналов:  и вычислим его спектральную плотность. По общему правилу:
и вычислим его спектральную плотность. По общему правилу:
 (2.18)
(2.18)
Применив обратное преобразование Фурье, выразим сигнал  через его спектральную плотность и подставим результат в (2.18):
через его спектральную плотность и подставим результат в (2.18):
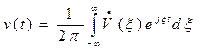

Изменив порядок интегрирования, будем иметь:

откуда:
 (2.19)
(2.19)
Интеграл, стоящий в правой части называют свёрткой функций V и U. Символически операция свёртки обозначается как *
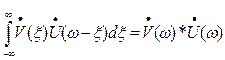
Таким образом, спектральная плотность произведения двух сигналов с точностью до постоянного числового множителя равна свёртке спектральных плотностей сомножителей:
 (2.20)
(2.20)
Операция свёртки коммутативна, т.е. допускает изменения порядка следования преобразуемых функций:
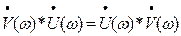
Теорема о свёртке может быть обращена: если спектральная плотность некоторого сигнала представляется в виде произведения  , причём
, причём 
 и
и  , то сигнал
, то сигнал  является свёрткой сигналов
является свёрткой сигналов  и
и 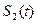 , но уже не в частной, а во временной области:
, но уже не в частной, а во временной области:
 (2.21)
(2.21)
VI. Теорема Планшереля
Пусть два сигнала  и
и 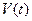 , в общем случае комплексные, определены своими обратными преобразованиями Фурье:
, в общем случае комплексные, определены своими обратными преобразованиями Фурье:
 ;
;
 .
.
Найдём скалярное произведение этих сигналов, выразив один из них, например  , через его спектральную плотность:
, через его спектральную плотность:
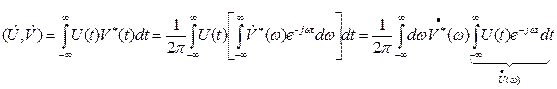
Здесь внутренний интеграл представляет собой спектральную плотность  сигнала
сигнала  поэтому:
поэтому:
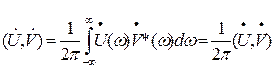 (2.22)
(2.22)
Скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей.

 причём
причём 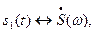
 , …, то взвешенная сумма сигналов преобразуется по Фурье следующим образом:
, …, то взвешенная сумма сигналов преобразуется по Фурье следующим образом: (2.11)
(2.11) - произвольные числовые коэффициенты.
- произвольные числовые коэффициенты. известно соответствие
известно соответствие 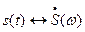 . Рассмотрим такой же сигнал, но возникающий на
. Рассмотрим такой же сигнал, но возникающий на  секунд позднее. Принимая точку
секунд позднее. Принимая точку  . Введём замену переменной:
. Введём замену переменной:  . Тогда
. Тогда  ,
, 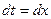
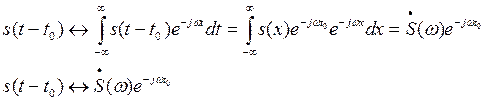
 при любых
при любых  играет новая независимая переменная
играет новая независимая переменная 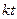 (
( - некоторое вещественное число.) Если
- некоторое вещественное число.) Если  > 1, то происходит “ сжатие” исходного сигнала; если же 0<
> 1, то происходит “ сжатие” исходного сигнала; если же 0<  , то:
, то: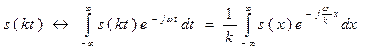
 , тогда
, тогда  , откуда следует:
, откуда следует: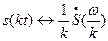 (2.13)
(2.13) заданы. Будем изучать новый сигнал
заданы. Будем изучать новый сигнал  и поставим цель найти его спектральную плотность
и поставим цель найти его спектральную плотность  .
. (2.14)
(2.14) (2.15)
(2.15) подставляя этот ряд в (2.15) и ограничиваясь первыми двумя числами, находим
подставляя этот ряд в (2.15) и ограничиваясь первыми двумя числами, находим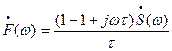
 (2.16)
(2.16) . Поэтому говорят, что мнимое число
. Поэтому говорят, что мнимое число  является неопределённым интегралом по отношению к функции
является неопределённым интегралом по отношению к функции  . Интеграл это есть
. Интеграл это есть  - его спектральная плотность, а
- его спектральная плотность, а  (2.17)
(2.17) служит оператором интегрирования в частотной области.
служит оператором интегрирования в частотной области. и
и  - два сигнала, для которых известны соответствия
- два сигнала, для которых известны соответствия  ,
,  .Образуем произведение этих сигналов:
.Образуем произведение этих сигналов:  и вычислим его спектральную плотность. По общему правилу:
и вычислим его спектральную плотность. По общему правилу: (2.18)
(2.18)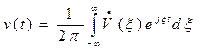


 (2.19)
(2.19)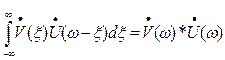
 (2.20)
(2.20)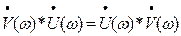
 , причём
, причём 
 и
и  , то сигнал
, то сигнал  является свёрткой сигналов
является свёрткой сигналов  и
и 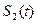 , но уже не в частной, а во временной области:
, но уже не в частной, а во временной области: (2.21)
(2.21) и
и 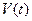 , в общем случае комплексные, определены своими обратными преобразованиями Фурье:
, в общем случае комплексные, определены своими обратными преобразованиями Фурье: ;
; .
.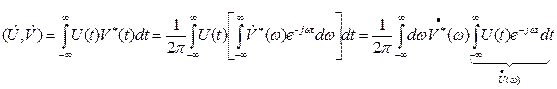
 сигнала
сигнала 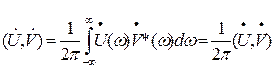 (2.22)
(2.22)


