Приближение локальной плотностиЕсли функция распределения Пусть требуется вычислить (интегральную) плотность состояний D (λ) для неупорядоченной цепочки, в которой среднее межатомное расстояние равно
Не следует думать, что такая оценка бесполезна. Например, в случае жидкости Кронига - Пенни это приближение подскажет нам, где искать главные «разрешенные» зоны и где могут быть запрещенные области энергии. Выберем теперь случайным образом конечный отрезок рассматриваемой цепочки, состоящий из L ячеек. Если среднее межатомное расстояние в нем равно
Эта аппроксимация дает гораздо более точные результаты, чем простая формула (37). Если функция
где s2 есть средний квадрат флуктуации межатомного расстояния при переходе от отрезка к отрезку. Точная форма функции Рассмотрим простую задачу для плотности числа колебаний в регулярной решетке с периодом a. Пусть
Тогда
Но т.к.
т.е. мы находим якобиан перехода от интегрирования по пространству K к интегрированию по w:
Рис. 6.6 Графики плотности числа состояний и интегральная плотность состояний в одномерных системах Особенность Ван-Хова:
(корневой характер плотности числа состояний в одномерных системах, в двухмерных системах - логарифмическая особенность). Итак, в одномерной регулярной решетке интегральная плотность состояний вблизи потолка первой зоны приближается к единице по закону
Однако при изменении межатомного расстояния
здесь Подставляя соотношения (6.32 – 34) в формулу (6.31), мы получаем выражение для интегральной плотности состояний в неупорядоченной цепочке. Итак,
где Под интегралом в (6.35) стоит произведение двух функций: плавной и с острым пиком. Для интегрирования используем метод перевала - в точке максимума плавная функция Например, достаточно далеко в запрещенной области энергии (выше
Рис. 6.7. Сравнение интегральной плотности состояний в модели «жидкости» Кронига - Пенни, вычисленной в приближении локальной плотности и путем расчета по методу Монте-Карло.
В действительности модель «одномерной жидкости» вряд ли заслуживает столь утонченного расчета, хотя следует отметить, что результаты таких вычислений совпадают с численными расчетами по методу Монте-Карло (рис. 6.7) в пределах ошибки. Таким образом, метод приближения локальной плотности очень полезен как эвристический, полуколичественный подход к расчету спектра неупорядоченной системы. Вместе с тем данный подход по-видимому не может служить исходной точкой для строго определенного ряда последовательных приближений, сходящихся к истинной плотности состояний. Далее, это приближение совершенно не годится для исследования «патологических» характеристик спектра вроде особых запрещенных областей энергии в модели бинарного сплава.
|

 непрерывно зависит от параметра беспорядка x, то спектр возбуждений можно найти приближенно. Если степень беспорядка не слишком велика, то спектр бесконечной цепочки, по-видимому, можно рассматривать как сумму независимых вкладов от различных коротких отрезков цепочки, концентрации компонентов сплава в которых различны. Таким образом, концепция «островков», уже позволившая дать качественную трактовку происхождения особых частот и запрещенных областей энергии в бинарном сплаве, обобщается на предмет полуколичественного описания полного спектра.
непрерывно зависит от параметра беспорядка x, то спектр возбуждений можно найти приближенно. Если степень беспорядка не слишком велика, то спектр бесконечной цепочки, по-видимому, можно рассматривать как сумму независимых вкладов от различных коротких отрезков цепочки, концентрации компонентов сплава в которых различны. Таким образом, концепция «островков», уже позволившая дать качественную трактовку происхождения особых частот и запрещенных областей энергии в бинарном сплаве, обобщается на предмет полуколичественного описания полного спектра. . В самом грубом приближении можно взять плотность состояний для регулярной цепочки с таким же межатомным расстоянием, т. е. принять:
. В самом грубом приближении можно взять плотность состояний для регулярной цепочки с таким же межатомным расстоянием, т. е. принять: . (6.30)
. (6.30) , то функция
, то функция  дает нам плотность состояний в идеальной цепочке с таким межатомным расстоянием. Будем далее рассматривать цепочку как последовательность отрезков идеальной цепочки. Пусть длины этих отрезков одинаковы и равны L, но средние межатомные расстояния в них
дает нам плотность состояний в идеальной цепочке с таким межатомным расстоянием. Будем далее рассматривать цепочку как последовательность отрезков идеальной цепочки. Пусть длины этих отрезков одинаковы и равны L, но средние межатомные расстояния в них  . Полученная таким путем плотность состояний для всей совокупности отрезков называется приближением локальной плотности:
. Полученная таким путем плотность состояний для всей совокупности отрезков называется приближением локальной плотности: . (6.31)
. (6.31) , (6.32)
, (6.32) , фигурирующей в формуле (6.38), зависит от конкретных свойств данной физической системы. Особенно интересны, однако, те области спектра, которые лежат вблизи точек, соответствующих краям зон в идеальной цепочке. Согласно теории функций, эти края зон должны совпадать с особенностями Ван Хова.
, фигурирующей в формуле (6.38), зависит от конкретных свойств данной физической системы. Особенно интересны, однако, те области спектра, которые лежат вблизи точек, соответствующих краям зон в идеальной цепочке. Согласно теории функций, эти края зон должны совпадать с особенностями Ван Хова. - жесткость связей атомов, имеющих массу M. Спектр колебаний определяется выражением:
- жесткость связей атомов, имеющих массу M. Спектр колебаний определяется выражением: или
или  .
. .
. , то можно сказать, что
, то можно сказать, что ,
, .
.
 (6.33)
(6.33) , соответствующая потолку указанной зоны, должна сдвигаться по какому-нибудь закону типа
, соответствующая потолку указанной зоны, должна сдвигаться по какому-нибудь закону типа , (6.34)
, (6.34) – потолок данной зоны для среднего (по всей цепочке) межатомного расстояния
– потолок данной зоны для среднего (по всей цепочке) межатомного расстояния  , а коэффициент
, а коэффициент  определяется конкретными параметрами модели. Предположим, что отклонения будут малы, поэтому оставим только линейный член.
определяется конкретными параметрами модели. Предположим, что отклонения будут малы, поэтому оставим только линейный член. ,
,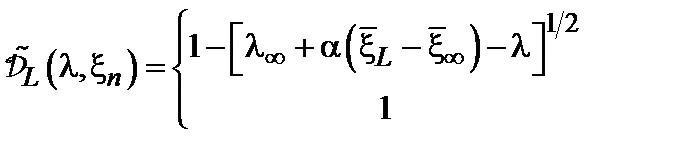 ,
, ,
, ,
,  ,
,  . (6.35)
. (6.35) заменяется на
заменяется на  и выносится за интеграл, а резкая функция интегрируется.
и выносится за интеграл, а резкая функция интегрируется. ) мы обнаруживаем экспоненциально затухающий хвост плотности состояний, описываемый выражением вида
) мы обнаруживаем экспоненциально затухающий хвост плотности состояний, описываемый выражением вида . (6.36)
. (6.36)



