Электропроводность вблизи порога протекания

 

Рассмотрим двумерные или трехмерные сетки с блокированными узлами. Как говорилось в начале главы, электропроводность таких сеток отлична от нуля при x > x_c и обращается в нуль на пороге протекания x_c. Экспериментальные данные, а также данные, полученные с помощью расчета на ЭВМ, показывают, что удельная электропроводность сеток обращается в нуль по закону

, (7.10)

где множитель по порядку величины равен удельной электропроводности сетки без блокированных узлов. Величина t называется критическим индексом электропроводности и является предметом очень тщательного изучения, преимущественно с помощью расчетов на ЭВМ. (В одном из последних расчетов, например, использовалась квадратная сетка, имеющая 800 × 800 узлов.) Установлено, что для двумерных сеток = 1.3, а для трехмерных = 1.6 ÷ 1.7.

Сеточная модель бесконечного кластера позволяет вывести формулу (7.10) и связать индекс t с индексом радиуса корреляции. Электрический ток течет только по бесконечному кластеру, причем именно по его скелету. В мертвых концах, прикрепленных к скелету лишь с одной стороны, тока нет. Если сделать электрический ток достаточно сильным, так чтобы проволока, по которой он течет, светилась, то в темноте скелет бесконечного кластера можно наблюдать визуально освещенные каналы на темном фоне. Вдали от порога вся сетка светится более или менее равномерно, вблизи порога расстояние между освещенными каналами увеличивается и, наконец, на самом пороге свечение совсем прекращается – ток через систему прервался.

Вычислим удельную электропроводность скелета бесконечного кластера. Следует иметь в виду, что это вычисление не может претендовать на правильный учет численных множителей. Оно позволяет лишь получить зависимость от x – x_c. Эта зависимость не изменится, если мысленно заменить неправильную и нерегулярную сеть идеальной сеткой с периодом, равным R.

Рис. 7.22. К оценке проводимости скелета бесконечного кластера

 

Рассмотрим сначала плоский случай (рис.7.22). Удельное сопротивление равно сопротивлению квадрата с единичной длиной. Число проволочек, пересекающих этот квадрат, равно 1/ R, где R – расстояние между проволочками, которое выражается формулой (7.7). Обозначим сопротивление одной проволочки, имеющей единичную длину, через . Все проволочки включены параллельно. Следовательно, удельное сопротивление

,

а удельная электропроводность

. (7.11)

Подставляя (7.7), получим

, (7.12)

где .

В трехмерном случае нужно вычислить удельное сопротивление проволочного каркаса, изображающего, например, простую кубическую решетку с периодом R (от типа решетки зависит лишь численный коэффициент). Удельное сопротивление равно сопротивлению кубика с единичной длиной ребра. Число параллельно соединенных проволочек, проходящих через грань такого кубика, равно 1/ R ². Поэтому удельное сопротивление

(7.13)

и удельная электропроводность равна:

, (7.14)

где .

Во избежание недоразумений следует обратить внимание на то, что удельная электропроводность в двумерном и трехмерном случаях имеет разную размерность. В двумерном случае она измеряется в Ом^–1, а в трехмерном – в Ом^–1·см^–1.

Множители и по порядку величины представляют собой удельные электропроводности двумерной и трехмерной сеток без блокированных узлов. Действительно, как видно из формул (7.11) и (7.13), удельная электропроводность превращается в или в при R = l, т.е. когда сетка бесконечного кластера совпадает с исходной сеткой, на которой ставится задача. Таким образом, величина в формуле (7.10) в двумерном случае равна , а в трехмерном – .

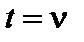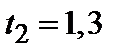Сравнивая формулы (7.11) и (7.12) с формулой (7.10), получаем, что в двумерном случае , а в трехмерном . Используя и , получим , , что очень близко к приведенным выше данным. Это совпадение свидетельствует в пользу модели Шкловского – де Жена.