Черт. 1координаты точки М через х и у (ОН = х, НМ = у) и выразим стороны треугольника ЕО и ОМ через х и у. Очевидно, что
и ЕО = ЕН — ОН. Обозначим
(так как ЕМ касательная к кривой в точке М и, следовательно,
Так как треугольник MEO равнобедренный, то
Равенство (6) представляет собой дифференциальное уравнение первого порядка, из которого надо найти ординату «у» кривой AВ, как функцию абсциссы, что и определит форму кривой сечения рефлектора. Уравнение (6) более сложное, чем в предыдущей задаче, поэтому решение этого уравнения будет проведено в §5 главы I, где будет указан прием решения уравнений такого типа. Задача 3. Имеется замкнутая электрическая цепь с сопротивлением R и силой тока I 0. В некоторый момент времени, которые мы примем за начальный (t = 0), постоянный ток I 0 размыкается. Требуется выяснить, прекратится ли сразу ток в цепи, а если нет то как он будет убывать. Выключение постоянной электродвижущей силы, поддерживавшей силу тока I 0 в цепи, вызывает, вследствие изменения магнитного поля тока I 0, возникновение электродвижущей силы индукции (явление самоиндукции). Таким образом, в цепи индуцируется ток под действием одной лишь электродвижущей силы самоиндукции; он называется «экстратоком размыкания». Экстраток размыкания направлен в ту же сторону, что и основной ток. Известно, что эта электродвижущая сила самоиндукции пропорциональна скорости изменения силы тока (коэффициент пропорциональности называется коэффициентом самоиндукции), т. е. имеет вид:
где I — переменная сила экстратока размыкания и L — коэффициент самоиндукции. По закону Ома имеем:
это равенство представляет собой дифференциальное уравнение первого порядка, из которого надо определить силу экстратока размыкания как функцию времени. Собираем в уравнении (7) члены, содержащие переменную I, в левую часть и члены, содержащие переменную t, в правую часть:
Как и в задаче 1, переписываем последнее равенство в виде:
откуда получаем:
(постоянную прибавляем в виде логарифма постоянной, так как это удобнее для дальнейших преобразований). Потенцируя, получаем:
что и дает искомое выражение силы экстратока размыкания через t. Опять-таки в условиях данной задачи можно выяснить, что постоянная С может иметь только одно вполне определенное значение. Для этого положим t = 0 в формуле (8), причем I обратится в I 0:
Подставляя полученное значение С в формулу (8), имеем:
Эта формула дает определенный ответ на вопрос, поставленный в задаче: при размыкании тока сила тока в цепи не сразу падает до нуля, а постепенно спадает по показательному закону (это уменьшение происходит быстро: например, если L= 0, 1 гн и R= 0, 7 ом, то за 0, 1 секунды сила тока при размыкании спадет до ½ I 0). Аналогичное исследование с помощью дифференциального уравнения можно провести и для изучения экстратока замыкания. Задача 4. Пусть два вещества A и В, находящиеся в растворе, вступают в необратимую химическую реакцию. Требуется найти формулу, по которой можно было бы подсчитать в любой момент времени количество вещества, уже вступившего в реакцию. Обозначим через а и b количества этих веществ (в грамм-молекулах на единицу объема) в начале реакции, т. е. при t = 0 (пусть, например, а< b), и через x — одинаковое количество того и другого вещества, уже вступившего в реакцию к моменту времени t. В этот момент времени в единице объема находится а—х грамм-молекул вещества А и b—х грамм-молекул вещества В. Известно, что по закону химического взаимодействия масс скорость химической реакции для некоторых типов реакций пропорциональна произведению (а—х)·(b—х). Так как скорость химической реакции есть скорость увеличения х, то она является производной от х по времени, и поэтому закон химического взаимодействия масс может быть записан следующим образом:
где к — коэффициент пропорциональности. Уравнение (10) есть дифференциальное уравнение первого порядка, где неизвестной является функция х (t). Для того чтобы найти эту функцию, поступим так же, как в задачах 1 и 3, а именно, отделим переменные t и х друг от друга, уединив члены с х в левой части уравнения и члены с t в правой:
Последнее равенство можно переписать в виде:
откуда:
Умножаем на (а—b):
и, потенцируя, получаем:
Обозначим для простоты второй постоянный множитель одной буквой
и найдем из (11) выражение искомой функции х (t) через время:
Конкретное числовое значение постоянной С1 для данной задачи можно найти опять-таки с помощью начальных условий: при t = 0, х = 0. Подставляем начальные условия в (12):
откуда
упрощая, получаем:
Эта формула и дает окончательное выражение для количества вещества, вступившего в реакцию к моменту времени t. Легко видеть, что при возрастании t величина х приближается к а. Задача 5. Гибкая однородная нерастяжимая нить подвешена за два конца и провисает под действием силы тяжести. Найти уравнение кривой, по которой происходит провисание. Выберем наиболее удобное расположение нити в координатной системе, указанное на чертеже 2, а именно: направим силу тяжести по отрицательному направлению оси ОY и расположим нить симметрично относительно оси ОY (числовое значение длины отрезка ОD = а будет указано ниже). Возьмем бесконечно малый участок нити от А до В длиной (в наших рассуждениях вместо бесконечно малых приращений переменных величин мы будем брать дифференциалы этих величин, так как бесконечно малые приращение и дифференциал функции разнятся друг от друга только бесконечно малыми высших порядков малости). Рассмотрим силы, действующие на этом участке: в точке А действует натяжение S влево от A; в точке В действует натяжение S+dS вправо от В; также на участке АВ действует сила тяжести, направленная вертикально вниз и по величине равная
где q —линейная плотность нити (по условию задачи q=const). Когда нить находится в состоянии равновесия, сумма всех сил, действующих на участке АВ, равна нулю. Разложим все силы на
|

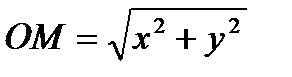
 и из прямоугольного треугольника МЕН получим:
и из прямоугольного треугольника МЕН получим: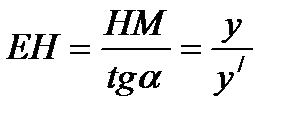 .
. ). Используя это равенство, получаем:
). Используя это равенство, получаем: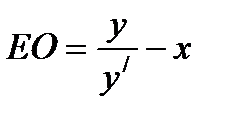 .
. . (6)
. (6) ,
, ; (7)
; (7) .
. ,
, .
.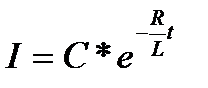 , (8)
, (8) , т. е.
, т. е.  .
. . (9)
. (9)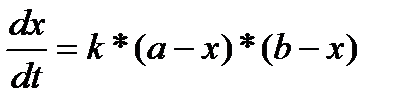 , (10)
, (10)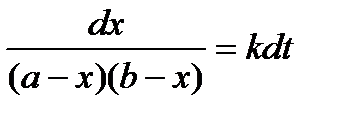 .
. ,
, .
.
 . (11)
. (11)
 ,
,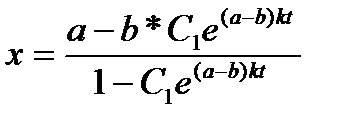 . (12)
. (12) ,
, .Подставляем найденное значение С1 в (12):
.Подставляем найденное значение С1 в (12):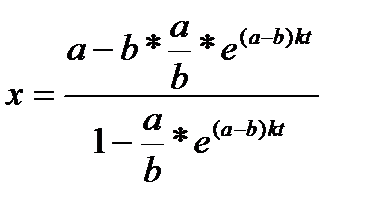 ,
, . (13)
. (13)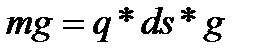 ,
,


