Основные определения. Напомним, что осевыми моментами инерции плоской фигуры относительно произвольных осей и называются величиныНапомним, что осевыми моментами инерции плоской фигуры относительно произвольных осей
Центробежным моментом инерции является величина
Оси называются центральными, если они проходят через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю. Главными осями инерции фигуры называются оси, относительно которых центробежный момент инерции равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью. Для вычисления моментов инерции относительно главных центральных осей надо уметь находить положение центра тяжести фигуры и знать, как изменяются моменты инерции при параллельном переносе и повороте осей. Напомним уже известные студенту формулы и приведем новые. Определение центра тяжести фигуры производится по формулам
где вспомогательные оси При параллельном переносе осей моменты инерции изменяются по следующим законам:
В формулах (5.16)–(5.18) При повороте осей (рис. 5.14) координаты точки меняются по известному закону
Подставляя эти формулы в (5.13)–(5.14), получим, что моменты инерции изменяются следующим образом:
Угол Чтобы найти, на какой угол
Подставляя найденный угол
Моменты инерции относительно главных осей имеют экстремальные значения среди бесконечного множества центральных осей: относительно одной оси момент инерции максимален, относительно другой имеет минимальное значение. Чтобы выяснить, какой момент инерции: максимальный или минимальный – имеет место для главной оси
Если при После определения моментов инерции относительно главных осей можно построить эллипс инерции – эллипс, полуоси которого равны радиусам инерции относительно главных осей. Радиус инерции В заключение приведем некоторые формулы для определения моментов простых фигур относительно центральных осей. Для прямоугольника (рис. 5.16, а) оси
Для круга (рис. 5.16, б) любая ось, проходящая через центр тяжести, является главной и
У прямоугольного треугольника (рис. 5.16, в) оси
На рис. 5.16, г показана фигура, представляющая собой четверть круга (квадрант круга). Для этой фигуры относительно центральных осей
Чтобы определить знак центробежного момента инерции треугольника или квадранта круга, надо использовать следующее правило знаков: если гипотенуза треугольника (дуги квадранта) в системе координат При определении моментов инерции фигуры, состоящей из прокатных профилей: двутавров, швеллеров, уголков (как в задаче № 31), осевые моменты инерции относительно собственных центральных осей двутавров, швеллеров, уголков берутся из таблиц прокатных профилей. Центробежные моменты инерции двутавров и швеллеров относительно собственных осей равны нулю. Центробежный момент инерции равнобоких уголков относительно осей
где
|

 и
и  называются величины
называются величины ;
;  . (5.13)
. (5.13)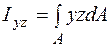 . (5.14)
. (5.14) ;
;  , (5.15)
, (5.15)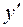 ,
,  , относительно которых вычисляются статические моменты, выбираются произвольно.
, относительно которых вычисляются статические моменты, выбираются произвольно.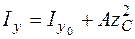 ; (5.16)
; (5.16) ; (5.17)
; (5.17) Рис. 5.13. Параллельный перенос осей
Рис. 5.13. Параллельный перенос осей
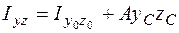 . (5.18)
. (5.18) ,
,  ,
, 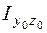 – моменты инерции относительно центральных осей;
– моменты инерции относительно центральных осей;  ,
,  – координаты центра тяжести (точки
– координаты центра тяжести (точки 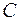 на рис. 5.13) в системе осей
на рис. 5.13) в системе осей  ,
, 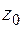 (см. рис. 5.13). Заметим, что если при вычислении осевых моментов инерции знаки координат не имеют значения, то при определении центробежного момента инерции знаки координат
(см. рис. 5.13). Заметим, что если при вычислении осевых моментов инерции знаки координат не имеют значения, то при определении центробежного момента инерции знаки координат  (5.19)
(5.19) ; (5.20)
; (5.20) ; (5.21)
; (5.21)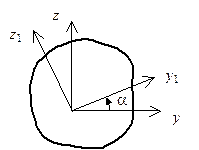 Рис. 5.14. Поворот осей
Рис. 5.14. Поворот осей
 . (5.22)
. (5.22) в формулах (5.20)–(5.22), на который поворачиваются оси, считается положительным, если он отсчитывается от положительного направления оси
в формулах (5.20)–(5.22), на который поворачиваются оси, считается положительным, если он отсчитывается от положительного направления оси  .
. надо повернуть оси, чтобы они стали главными осями инерции, положим согласно определению главных осей центробежный момент инерции по (5.22) равным нулю. Тогда
надо повернуть оси, чтобы они стали главными осями инерции, положим согласно определению главных осей центробежный момент инерции по (5.22) равным нулю. Тогда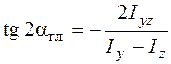 . (5.23)
. (5.23) . (5.24)
. (5.24)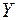 , повернутой на угол
, повернутой на угол  , определяемой формулой (5.20). Вычислим эту производную:
, определяемой формулой (5.20). Вычислим эту производную: . (5.25)
. (5.25) Рис. 5.15. Эллипс
инерции
Рис. 5.15. Эллипс
инерции
 вторая производная
вторая производная  , то относительно оси
, то относительно оси  ), если
), если  , то
, то  .
. откладывается вдоль главной оси
откладывается вдоль главной оси  , а
, а  – вдоль оси
– вдоль оси  ;
; 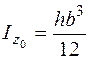 ;
;  . (5.26)
. (5.26)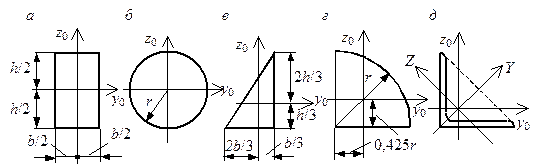 Рис. 5.16. К определению моментов инерций простых фигур
Рис. 5.16. К определению моментов инерций простых фигур
 ;
;  ;
;  ;
;  . (5.28)
. (5.28)
 ;
; 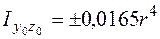 . (5.29)
. (5.29) , квадрант круга, изображенный на рис. 5.16, г, имеет отрицательный центробежный момент инерции.
, квадрант круга, изображенный на рис. 5.16, г, имеет отрицательный центробежный момент инерции. , параллельных полкам, определяется по формуле
, параллельных полкам, определяется по формуле , (5.29а)
, (5.29а) ,
,  – моменты инерции относительно главных центральных осей
– моменты инерции относительно главных центральных осей  уголка (рис. 5.16, д) – находятся по таблице прокатных профилей. Выбор знака в формуле (5.29а) производится по той же схеме, что и для треугольника или квадранта круга: если линия, соединяющая крайние точки уголка (пунктир на рис. 5.16, д), описывается возрастающей функцией в системе координат
уголка (рис. 5.16, д) – находятся по таблице прокатных профилей. Выбор знака в формуле (5.29а) производится по той же схеме, что и для треугольника или квадранта круга: если линия, соединяющая крайние точки уголка (пунктир на рис. 5.16, д), описывается возрастающей функцией в системе координат 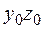 , то
, то 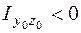 .
.


