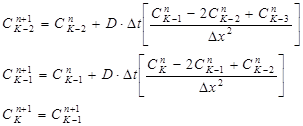Явная разностная схемаРассмотрим исходное уравнение (165) в n -й момент времени в k -ой точке пространства. Тогда правая часть уравнения (165) – первая частная производная по времени будет представлена так:
Поскольку производная по времени, поэтому изменяется индекс n. Вторая частная производная в сеточной области определяется как отношение разности 1-х производных по длине шага сетки.
С помощью этих равенств производная Производим замену в уравнении (165).
Из (174) видно, что по значению функции c(x, t) в точках n -го временного слоя можно вычислить значение функции c(x, t) в точках n+ 1 временного слоя, т. е. мы имеем явную схему (рис. 104).
Рис. 104. Явная схема Значение c(x, t) при t=0 определяется из начальных условий: Значение функции с(x, t) в крайних узлах при х =0 и х = L определяется из краевых условий: 1. 2. Для расчета концентраций в сеточной области также необходимо знать CKn – концентрацию на границе (L) (концентрацию на парвом конце сетки), которая вычисляется из граничного условия:
откуда следует, что
Последовательно вычисляя С (xк, t 1) для Таким образом, уравнение (174) представляет собой систему уравнений, которая рассчитывается
|

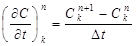 . (171)
. (171) . (172)
. (172) с 1-м порядком точности относительно шага Dt и частная производная
с 1-м порядком точности относительно шага Dt и частная производная 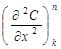 со 2-м порядком точности относительно шага Dx аппроксимируется в конечно-разностные отношения.
со 2-м порядком точности относительно шага Dx аппроксимируется в конечно-разностные отношения. . (173)
. (173) . (174)
. (174)
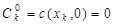 для
для  (нижняя граница сетки).
(нижняя граница сетки). для
для  (левая граница сетки).
(левая граница сетки). ,
,
 .
.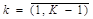 , затем C (xк, t 2) для
, затем C (xк, t 2) для  раз:
раз: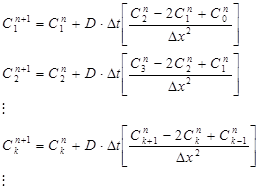 (175)
(175)