Ядерные реакции
Ядерной реакцией называется процесс сильного взаимодействия атомного ядра с элементарной частицей или с другим ядром, приводящий к преобразованию ядра (или ядер). Взаимодействие реагирующих частиц возникает при их сближении до расстояний порядка 10-15м благодаря действию ядерных сил. Наиболее распространенным видом ядерной реакции является взаимодействие легкой частицы а с ядром X, в результате которого образуется легкая частица b и ядро Y: Х + а ® Y + b. Уравнение таких реакций принято записывать сокращенно в виде Х(а, b)Y. (44) В качестве легких частиц а и b могут фигурировать нейтрон (n), протон (р), дейтрон (d), a-частица (a) и g-фотон (g). Ядерные реакции могут сопровождаться как выделением, так и поглощением энергии. Количество выделяющейся энергии Q называется энергией реакции. Она определяется разностью масс исходных и конечных ядер (частиц):
где å m1 – сумма масс ядер, вступающих в реакцию, å m2 – сумма масс ядер, получившихся в результате реакции. Если сумма масс образующихся ядер превосходит сумму масс исходных ядер, реакция идет с поглощением энергии и энергия реакции будет отрицательной (Q< 0).
Примеры решения задач
а) По закону Стефана – Больцмана определим энергетическую светимость Солнца:
где б) Поток энергии, излучаемый Солнцем, найдем, умножив энергетическую светимость на площадь поверхности Солнца: Фэ = Rэ× S = Rэ× 4p× Rc2, где Rc = 6, 95× 108 м – радиус Солнца. Фэ = 3, 9× 1026 Вт. в) Длину волны, на которую приходится максимум спектральной плотности энергетической светимости, найдем из закона смещения Вина: lmax = b/T, где b =, 3× 10-3 м× К, lmax = 5× 10-7 м = 500 нм. г) Энергия, излучаемая Солнцем за время t, будет равна W = Фэ× t. Для t = 1 мин, W» 2, 34× 1028 Дж.
Для определения светового давления на зеркальце используем следующую формулу:
где с=3× 108 м/с – скорость света в вакууме, r – коэффициент отражения света (для зеркальных поверхностей, если нет специальных указаний, считать r = 1). Силу светового давления определим, умножив давление света на площадь поверхности зеркальца (pd2/4):
Решение
Для установления связи между энергиями фотона до и после рассеяния воспользуемся формулой Комптона
Энергия фотона e = hn = hc/l. Отсюда l1 = hc/e1 и l2 = hc/e2. После подстановки в формулу Комптона получим
Разделим последнее равенство на hc и обозначим энергию покоя электрона mc2 = E0.
1/e2 – 1/e1 = 2/E0.
Часть первоначальной энергии фотона e1 приходится на электрон отдачи eе, а другая – на рассеянный фотон e2: e1 = eе + e2. С учетом последнего равенства получим:
Умножим на e1:
Решая последнее уравнение, получаем
Решение
1/l = R(1/m2 – 1/n2).
Таким образом, при обратном переходе с 5-го уровня электроны могут переходить на 1, 2, 3, 4-й уровни. Этим переходам будут соответствовать определенные спектральные линии: Всего будет наблюдаться 10 линий: 4 линии в серии Лаймана; 3 – в серии Бальмера; 2 – в серии Пашена; 1 – в серии Брэккета.
5. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 0, 5 кВ. Принимая, что неопределенность импульса равна 0, 1 % от его численного значения, найти неопределенность координаты электрона. Являются ли в данных условиях электроны квантовыми или классическими частицами?
Решение Согласно соотношению неопределенностей, DxDpx ³ где Dx – неопределенность координаты электрона; Dpx – неопределенность проекции его импульса; T = |e|U = 0, 5 кэВ, то есть электрон при данных условиях не является релятивистской частицей и импульс электрона:
Согласно условию задачи, неопределенность импульса Dpx = 0, 001px = 1, 24× 10-26 кг× м/с, то есть Dpx< < px, и электрон при данных условиях является классической частицей. Искомая неопределенность координаты из выражения (1):
.
Решение Собственное значение энергии электрона, находящегося на n-м энергетическом уровне в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»:
где m=9, 11× 10-31 кг – масса электрона; Минимальную энергию электрон имеет при минимальном n, то есть при n = 1:
Вероятность обнаружить частицу в интервале x1< x< x2:
где Возбужденному состоянию n = 4 отвечает собственная функция:
Тогда по условию задачи:
Заменив sin2(4px/ l) = 1/2× (1 – cos(8px/ l)), запишем
График зависимости
7. Первоначальная масса радиоактивного изотопа радона
Решение Начальная активность изотопа A0 = lN0, где
где M – молярная масса радона (M=222× 10-3 кг/моль); NA – число Авогадро, равное 6, 02× 1023 моль-1. Учитывая это выражение, найдем искомую начальную активность изотопа:
Активность изотопа A = lN, где, согласно закону радиоактивного распада, N = N0e-lt – число нераспавшихся ядер в момент времени t. Учитывая lN0 = A0, найдем, что активность нуклида уменьшается со временем по закону: A = A0e-lt =
8. В результате соударения дейтрона с ядром бериллия
Решение Из законов сохранения электрического заряда и массовых чисел следует, что Z = 5, A = 10, то есть образовавшееся в результате ядерной реакции ядро – изотоп бора реакцию можно записать в виде
Энергетический эффект реакции:
где в первых круглых скобках указаны массы исходных ядер, во вторых – массы ядер продуктов реакции.
с=3× 108 м/с. Вычисляя, получим Q = 4, 84 МэВ, энергетический эффект положительный; реакция экзотермическая.
Задачи для самостоятельного решения 1. Определить энергию, излучаемую за одну минуту из смотрового окошка площадью 8 см2 плавильной печи, если ее температура 1200К. Ответ: W = 5, 65 кДж. 2. Определить красную границу lкр фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом с длиной волны l = 400нм максимальная скорость фотоэлектронов umax = 0, 65 Мм/с Ответ: lкр = 651 нм. 3. Определить минимальную длину волны в сплошном спектре рентгеновских лучей, если рентгеновская трубка работает под напряжением U = 30 кВ. Ответ: lmin= 41 пм. 4. Определить энергию фотона, соответствующего второй линии в первой инфракрасной серии (серии Пашена) атома водорода. Ответ: e = 0, 97 эВ. 5. Определить длину волны де Бройля lБ электрона, прошедшего ускоряющую разность потенциалов U = 700 кВ является ли электрон при этих условиях релятивистской частицей (энергия покоя электрона E0 = m0c2 = 0, 512 МэВ, m0 = 9, 11× 10-31 кг, с = 3× 108 м/с, е = 1, 6× 10‑ 19 Кл)? Ответ: lБ = 1, 13пм. Это релятивистский случай.
6. Две частицы, электрон и протон, обе с энергией Е = 5эВ, движутся в положительном направлении оси x, встречая на своем пути потенциальный барьер высотой U = 10эВ и ширины l = 1пм. Определить отношение вероятностей прохождения частицами этого барьера.
где me = 9, 11× 10-31 кг; mp = 1, 672× 10-27 кг;
7. Какой изотоп образуется из радиоактивного изотопа 3Li8 после одного b-распада и одного a-распада? Ответ: 2He4.
8. Написать недостающие обозначения в следующих ядерных реакциях:
Ответ:
Контрольные задания
601. Определить температуру, при которой энергетическая светимость черного тела равна 10 кВт/м2. 602. Определить относительное увеличение DRэ /Rэ энергетической светимости черного тела при увеличении его температуры на 1 %. 603. Во сколько раз надо увеличить абсолютную температуру черного тела, чтобы его энергетическая светимость возросла в два раза? 604. Найти величину солнечной постоянной, т.е. количество лучистой энергии, посылаемой Солнцем ежеминутно через площадку в 1 см2, находящуюся перпендикулярно к солнечным лучам на таком же расстоянии от него, что и Земля. 605. Мощность излучения абсолютно черного тела равна 10 кВт. Найти площадь излучающей поверхности тела, если известно, что длина волны, на которую приходится максимум спектральной плотности его энергетической светимости, равна 7× 10-7 м. 606. На какую длину волны приходится максимум спектральной плотности энергетической светимости черного тела при температуре t = 0 °C? 607. Определить температуру черного тела, при которой максимум спектральной плотности энергетической светимости приходится на красную границу видимого спектра l = 750 нм. 608 При увеличении абсолютной температуры черного тела в два раза (T2 = 2T1) длина волны, на которую приходится максимум спектральной плотности энергетической светимости, уменьшилась на 400 нм. Определить начальную и конечную температуры T1 и T2. 609. Длина волны, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, равна 0, 85 мкм. Определить энергетическую светимость тела. 610. Температура абсолютно черного тела изменилась от 727 до 1727 °С. Во сколько раз при этом изменилась мощность излучения? 611. Определить работу выхода для натрия в электрон-вольтах, если красная граница фотоэффекта для него lкр = 500 нм. 612. Будет ли наблюдаться фотоэффект, если на поверхность серебра направить ультрафиолетовое излучение с длиной волны 300 нм? 613. На поверхность лития падает монохроматический свет с длиной волны 310 нм. Чтобы прекратить эмиссию электронов, нужно приложить между катодом и анодом задерживающую разность потенциалов 1, 7 В. Определить работу выхода для лития. 614. Кванты света с энергией 4, 9 эВ вырывают электроны из металла с работой выхода 4, 5 эВ. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона. 615. При фотоэффекте с платиновой поверхности величина задерживающего потенциала оказалась равной 0, 8 В. Найти длину волны применяемого излучения и максимальную длину волны, при которой еще возможен фотоэффект. 616. Определить поверхностную плотность потока энергии излучения, падающего на зачерненную поверхность, если световое давление на эту поверхность при перпендикулярном падении лучей равно 10 мкПа. 617. Давление монохроматического света с длиной волны 600 нм на черную поверхность, расположенную перпендикулярно падающим лучам, равно 0, 1 мкПа. Определить число фотонов, падающих за 1 с на поверхность площадью 1 см? 618. На поверхность площадью 100 см2 ежеминутно падает световая энергия 63 Дж. Найти величину светового давления когда поверхность 1) полностью отражает все лучи; 2) полностью поглощает все лучи. 619. Колба электрической лампы представляет собой сферу радиусом 3 см. Часть стенки колбы изнутри посеребрена. Лампа потребляет мощность 60 Вт, 80 % которой затрачивается на излучение. Определить световое давление на посеребренную часть стенки колбы с коэффициентом отражения, равным 0, 8. 620. Световой поток мощностью 9 Вт нормально падает на поверхность площадью 10 см2, коэффициент отражения которой равен 0, 8. Какое давление испытывает при этом данная поверхность? 621. Фотон с энергией 0, 15 МэВ испытал рассеяние на покоившемся свободном электроне, в результате чего его длина волны увеличилась на 1, 5 пм. Найти угол j, под которым вылетел комптоновский электрон отдачи. 622. Рентгеновское излучение с длиной волны 55, 8 пм рассеивается плиткой графита (комптон-эффект). Определить длину волны излучения, рассеянного под углом J=60О к направлению падающего пучка. 623. Фотон с энергией 0, 4 МэВ рассеялся под углом J=30о на свободном электроне. Определить энергию рассеянного фотона и кинетическую энергию электрона отдачи. 624. Определить импульс электрона отдачи при эффекте Комптона, если фотон с энергией, равной энергии покоя электрона, был рассеян на угол J=180о.
625. Определить энергию, массу и импульс фотона с длиной волны 1, 6 пм. 626. С какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны 520 нм? 627. Найти массу фoтона, импульс которого равен импульс равен импульсу молекулы водорода при температуре 20 °С. Скорость молекулы считать равной средней квадратичной скорости. 628. К электродам рентгеновской трубки приложена разность потенциалов 60 кВ. Наименьшая длина волны рентгеновских лучей, получаемых от этой трубки, равна 19, 4 пм. Найти из этих данных постоянную Планка. 629. Найти коротковолновую границу непрерывного рентгеновского спектра, если известно, что уменьшение приложенного к рентгеновской трубке напряжения на 23 кВ увеличивает искомую длину волны в два раза. 630. Какую разность потенциалов надо приложить к рентгеновской трубке, чтобы получить рентгеновские лучи с длиной волны 1, 6 пм? 631. Определить частоту обращения электрона на второй орбите атома водорода. 632. Определить потенциал ионизации атома водорода. 633. Определить первый потенциал возбуждения атома водорода. 634. Определить длину волны, соответствующую третьей спектральной линии в серии Бальмера. 635. Вычислить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый. 636. Найти период обращения электрона на третьей орбите в атоме водорода. 637. Сколько спектральных линий и в каких сериях будет испускать атом водорода, который возбуждают до 6-го энергетического состояния? 638. Найти радиус первой боровской орбиты электрона для однократно ионизированного гелия и скорость электрона на ней. 639. Найти первый потенциал возбуждения однократно ионизированного гелия. 640. Определить наибольшую и наименьшую длины волн в первой инфракрасной серии спектра водорода (серии Пашена). 641. Определить длину волны де Бройля lБ для электрона, находящегося в атоме водорода на третьей боровской орбите. 642. Определить длину волны де Бройля lБ для нейтрона, движущегося со средней квадратичной скоростью при Т = 290 К. 643. Протон движется в однородном магнитном поле с индукцией В = 15 мТл по окружности радиусом R = 1, 4 м. Определить длину волны де Бройля lБ для протона. 644. Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля lБ для него была равна 1 нм. 645. Кинетическая энергия электрона равна 1 кэВ. Определить длину волны де Бройля. 646. Электронный пучок выходит из электронной пушки пoд воздействием разности потенциалов U = 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 пм и его скорость с точностью до 10 %.
647. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10 % от его числового значения, определить неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории? 648. Воспользовавшись соотношением неопределенности, оценить размытость энергетического уровня DЕ в атоме водорода в электрон-вольтах: 1) для основного состояния; 2) для возбужденного состояния (время его жизни Dt = 10-8 с.); 649. Длина волны l излучаемого атомом фотона составляет 0, 6 мкм. Принимая время жизни возбужденного состояния Dt = 10-8 с, определить отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом DЕ/Е. 650. Принимая, что электрон находится внутри атома диаметром 0, 3 нм, определить (в электрон-вольтах) неопределенность энергии этого электрона. 651. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n=2). Определить вероятность обнаружения частицы в области 3/8 l £ C£ 5/8 l. 652. Электрон находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «cтенками». Определить вероятность нахождения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 3). 653. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «cтенками» находится в основном состоянии. Определить вероятность обнаружения частицы в левой трети «ямы». 654. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «cтенками» находится в возбужденном состоянии (n=3). Определить, в каких точках «ямы» (0 £ C£ l) плотность вероятности обнаружения частицы максимальна. Пояснить полученный результат графически. 655. Для условия задачи 654 определить, в каких точках «ямы» (0 £ C£ l) плотность вероятности обнаружения частицы минимальна. Пояснить полученный результат графиком. 656. Электрон с энергией E = 4 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высоты U = 10 эВ и шириной l = 0, 1 нм. Определить коэффициент D прозрачности потенциального барьера. 657. Прямоугольный потенциальный барьер имеет ширину l = 0, 1 нм. Определить в электрон-вольтах разность энергии U – E, при которой вероятность прохождения электрона сквозь барьер составит 0, 5. 658. Протон с энергией E = 5 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0, 1 нм. Определить вероятность прохождения протоном этого барьера. 659. Во сколько раз надо сузить ширину барьера в условии задачи 658, чтобы вероятность прохождения барьера протоном стала равна 0, 5? 660. Прямоугольный потенциальный барьер имеет ширину l = 0, 1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси x электрона U – E = 5 эВ. Определить, во сколько раз изменится коэффициент прозрачности барьера D для электрона, если разность U – E возрастет в 4 раза. 661. Первоначальная масса радиоактивного изотопа йода 662. Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определить его активность по истечении промежутка времени, равного половине периода полураспада. 663. Начальная активность 1 г изотопа радия 664. Определить период полураспада Т1/2 некоторого радиоактивного изотопа, если его активность за 5 сут уменьшилась в 2, 2 раза. 665. Определить удельную активность p (число распадов в 1 с на 1 кг вещества) изотопа 666. Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается 667. Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается 668. Определить, сколько a- и b-частиц выбрасывается при превращении ядра таллия 669. Радиоактивный изотоп радия 670. Какой изотоп образуется из 671. Определить энергетический эффект реакции 672. Определить энергетический эффект реакции 673. Определить зарядовое число Z и массовое число А частицы, обозначенной буквой C, в символической записи ядерной реакции:
674. Записать недостающие обозначения C в следующих реакциях:
675. Дополнить недостающие обозначения C в следующих ядерных реакциях:
676. Определить число нейтронов, возникающих за 1 с в ядерном реакторе тепловой мощностью Р = 200 МВт, если известно, что при одном акте деления выделяется энергия Е = 200 МэВ, а среднее число нейтронов на один акт деления составляет 2, 5. 677. Какое количество воды можно нагреть от 0 °C до кипения, если использовать все тепло, выделяющееся при реакции 678. Какое количество энергии в киловатт-часах можно получить от деления 1 г урана 679. Какое количество урана 680. При взрыве водородной бомбы протекает термоядерная реакция образования гелия из дейтерия и трития. Написать эту реакцию, найти ее энергетический эффект. Какое количество энергии можно получить при образовании 1 г гелия?
Варианты контрольных заданий
|

 (45)
(45) 1. Считая излучение Солнца близким к излучению абсолютно черного тела, определить энергетическую светимость Солнца, поток энергии, излучаемый Солнцем, длину волны, на которую приходится максимум спектральной плотности энергетической светимости и энергию, излучаемую Солнцем за 1 минуту. Температура поверхности Солнца принять равной 5800К.
1. Считая излучение Солнца близким к излучению абсолютно черного тела, определить энергетическую светимость Солнца, поток энергии, излучаемый Солнцем, длину волны, на которую приходится максимум спектральной плотности энергетической светимости и энергию, излучаемую Солнцем за 1 минуту. Температура поверхности Солнца принять равной 5800К. Решение
Решение Rэ = sT4,
Rэ = sT4, , Rэ = 6, 42× 107 Вт/м2.
, Rэ = 6, 42× 107 Вт/м2. 2. Поток энергии, излучаемый электрической лампой, N = 600 Вт. На расстоянии r = 1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d = 2 см. Принимая лампу за точечный источник, определить силу F светового давления на зеркальце.
2. Поток энергии, излучаемый электрической лампой, N = 600 Вт. На расстоянии r = 1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d = 2 см. Принимая лампу за точечный источник, определить силу F светового давления на зеркальце. Решение
Решение Если принять лампу за точечный источник, то следует считать, что излучение лампы одинаково во всех направлениях. То есть энергия, излучаемая лампой за одну секунду, на расстоянии r от нее равномерно распределится по поверхности сферы радиусом r. Тогда плотность потока энергии излучения равна:
Если принять лампу за точечный источник, то следует считать, что излучение лампы одинаково во всех направлениях. То есть энергия, излучаемая лампой за одну секунду, на расстоянии r от нее равномерно распределится по поверхности сферы радиусом r. Тогда плотность потока энергии излучения равна: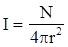 .
.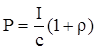 ,
, .
.
 3. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол J=180о? Энергия фотона до рассеяния равна 0, 255 МэВ.
3. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол J=180о? Энергия фотона до рассеяния равна 0, 255 МэВ. Обозначим e1 и e2 энергии фотона до и после рассеяния соответственно; l1 и l2 – длина волн соответствующих фотонов.
Обозначим e1 и e2 энергии фотона до и после рассеяния соответственно; l1 и l2 – длина волн соответствующих фотонов. , так как cos180о = – 1.
, так как cos180о = – 1. ×
× .
.

 4. Атом водорода освещается излучением с длиной волны 94 нм. Определить, какие спектральные линии появятся в спектре атома водорода.
4. Атом водорода освещается излучением с длиной волны 94 нм. Определить, какие спектральные линии появятся в спектре атома водорода.
 При возбуждении атома электрон в атоме переходит из основного состояния (m = 1) в состояние с главным квантовым числом n, которое можно определить по формуле:
При возбуждении атома электрон в атоме переходит из основного состояния (m = 1) в состояние с главным квантовым числом n, которое можно определить по формуле: (округляем до меньшего целого).
(округляем до меньшего целого).
 /2, (1)
/2, (1) =1, 054× 10-34 Дж× с – постоянная Планка. Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U:
=1, 054× 10-34 Дж× с – постоянная Планка. Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U: .
. .
.
 6. Электрон в одномерной прямоугольной «потенциальной яме» шириной l = 200 пм с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 4). Определить: 1) минимальную энергию электрона; 2) вероятность W обнаружения электрона в первой четверти «ямы».
6. Электрон в одномерной прямоугольной «потенциальной яме» шириной l = 200 пм с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 4). Определить: 1) минимальную энергию электрона; 2) вероятность W обнаружения электрона в первой четверти «ямы». ,
, – постоянная Планка.
– постоянная Планка. .
.
 – нормированная собственная волновая функция, соответствующая данному состоянию.
– нормированная собственная волновая функция, соответствующая данному состоянию. .
.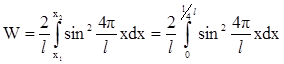 .
.
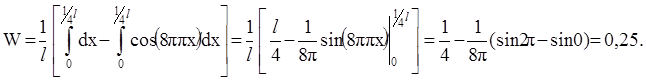


 (период полураспада T1/2 = 3, 82 сут.) равна 1, 5 г. Определить: 1) начальную активность изотопа; 2) его активность через 5 суток.
(период полураспада T1/2 = 3, 82 сут.) равна 1, 5 г. Определить: 1) начальную активность изотопа; 2) его активность через 5 суток.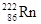 m0 = 1, 5 г
T1/2 = 3, 82 сут
t = 5 сут
m0 = 1, 5 г
T1/2 = 3, 82 сут
t = 5 сут
 – постоянная радиоактивного распада; N0 –число ядер изотопа в начальный момент времени.
– постоянная радиоактивного распада; N0 –число ядер изотопа в начальный момент времени. ,
, .
. .
. образовались новое ядро и нейтрон. Определить порядковый номер и массовое число образовавшегося ядра, записать ядерную реакцию и определить ее энергетический эффект.
образовались новое ядро и нейтрон. Определить порядковый номер и массовое число образовавшегося ядра, записать ядерную реакцию и определить ее энергетический эффект.
 . Поэтому ядерную
. Поэтому ядерную .
. , (1)
, (1)
 .
.
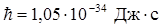 .
.

 (период полураспада Т1/2 = 8сут) равна 1 г. Определить: 1) начальную активность изотопа; 2) его активность через 3 сут.
(период полураспада Т1/2 = 8сут) равна 1 г. Определить: 1) начальную активность изотопа; 2) его активность через 3 сут. равна 1 Ки. Определить период полураспада Т1/2 этого изотопа.
равна 1 Ки. Определить период полураспада Т1/2 этого изотопа. , если период его полураспада Т1/2 = 4, 5× 109 лет.
, если период его полураспада Т1/2 = 4, 5× 109 лет. после трех a- и двух b--распадов.
после трех a- и двух b--распадов. после шести a- и трех b--распадов.
после шести a- и трех b--распадов. в ядро свинца
в ядро свинца  .
. претерпевает четыре a-распада и два b--распада. Определить для конечного ядра: 1) зарядовое число Z; 2) массовое число А.
претерпевает четыре a-распада и два b--распада. Определить для конечного ядра: 1) зарядовое число Z; 2) массовое число А. после четырех a-распадов и двух b-распадов?
после четырех a-распадов и двух b-распадов? .
. .
.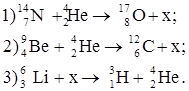


 , при полном разложении 1 г лития? Св=4, 19× 10 3 Дж/(кг× К).
, при полном разложении 1 г лития? Св=4, 19× 10 3 Дж/(кг× К). , если при каждом делении выделяется энергия, приблизительно равная 200 МэВ?
, если при каждом делении выделяется энергия, приблизительно равная 200 МэВ? расходуется в сутки на атомной электростанции мощностью 5× 103 кВт? КПД принять равным 17 %. Считать, что при каждом акте распада выделяется энергия 200 МэВ.
расходуется в сутки на атомной электростанции мощностью 5× 103 кВт? КПД принять равным 17 %. Считать, что при каждом акте распада выделяется энергия 200 МэВ.


