Точность в типовых режимахДля оценки точности системы регулирования используется величина ошибки в различных типовых режимах. Рассмотрим четыре наиболее распространенных режима. 1. Неподвижное состояние. В качестве типового режима рассматривается установившееся состояние при постоянных значениях управляющего и возмущающего воздействий. Ошибка системы в этом случае называется статической. Величина ошибки может быть найдена из общего выражения (4.15). Для этого необходимо, чтобы
Первое слагаемое представляет собой составляющую статической ошибки, определяемую управляющим воздействием. Эта составляющая может быть отличной от нуля только при статическом регулировании. При астатическом регулировании она обращается в нуль. Однако в подавляющем большинстве случаев первое слагаемое (7.2) может быть обращено в нуль и в статических системах посредством соответствующего масштабирования или использования неединичных обратных связей. Поэтому практически первая составляющая статической ошибки всегда может быть принята равной нулю. Второе слагаемое (7.2) никогда не обращается в нуль, так как даже использование регулирования с астатизмом высокого порядка может обратить в нуль лишь часть слагаемых, находящихся под знаком суммы. При выводе выражения (7.2) было оставлено без внимания следующее обстоятельство. Предполагалось, что чувствительный элемент, определяющий разность между требуемым и действительным значениями регулируемой величины, является идеальным и определяет имеющуюся ошибку в соответствии с выражением (7.1). В действительности чувствительному элементу как измерительному органу присущи свои ошибки. Принципиально ошибку чувствительного элемента можно рассматривать так же, как некоторое возмущающее воздействие и считать, что она входит во второе слагаемое (7.2). Однако на практике удобнее эту ошибку рассматривать отдельно и считать, что статическая ошибка
где 2. Движение с постоянной скоростью. В качестве второго типового режима используется движение системы с постоянной скоростью V = const, которое будет наблюдаться в установившемся состоянии при управляющем воздействии, изменяющемся по закону
Второе слагаемое этого выражения дает статическую ошибку (при условии, что возмущающие воздействия такие же, как в неподвижном положении системы), в которой может быть также учтена ошибка чувствительного элемента (7.3) Первое слагаемое (7.4) имеет смысл только при астатизме первого порядка, то есть в том случае, когда передаточная функция разомкнутой системы может быть представлена в виде
Тогда выражение (7.4) приводится к виду
Таким образом, в этом типовом режиме установившаяся ошибка будет слагаться из статической ошибки и добавочной скоростной ошибки, равной отношению скорости к добротности системы по скорости
Так как система может двигаться с различными скоростями, то качество ее удобнее характеризовать не самой скоростной ошибкой, которая является переменной величиной, а значением добротности по скорости
В статических системах первое слагаемое (7.6) стремится к бесконечности, а при астатизме выше первого порядка – к нулю. Поэтому режим движения с постоянной скоростью используется для оценки точности только систем регулирования с астатизмом первого порядка, главным образом, следящих систем, для которых такой режим является характерным. 3. Движение с постоянным ускорением. В качестве третьего типового режима используется установившееся движение системы регулирования с постоянным ускорением а = const. В этом случае управляющее воздействие меняется по закону Аналогично изложенному ранее, установившееся значение ошибки в этом режиме может быть найдено из выражения
Второе слагаемое (7.9), как и ранее, дает статическую ошибку. Первое слагаемое (7.9) имеет смысл только при астатизме второго порядка, когда передаточная функция разомкнутой системы может быть представлена в виде
Тогда выражение (7.9) приводится к виду
Первое слагаемое (7.11) представляет собой добавочную ошибку от постоянного ускорения. Как и в предыдущем случае, качество системы может быть оценено по величине добротности по ускорению
Этот типовой режим используется только для систем регулирования с астатизмом второго порядка, главным образом, следящих систем. 4. Движение по гармоническому (синусоидальному) режиму. Такой режим используется весьма часто, так как он позволяет наиболее полно оценить динамические свойства системы регулирования. Управляющее воздействие принимается изменяющимся по закону
В зависимости от конкретного вида системы регулирования, возмущающие воздействия в рассматриваемом режиме могут оставаться постоянными или меняться. Случай постоянства возмущающих воздействий приводит, как и в рассмотренных ранее втором и третьем типовых режимах, к появлению некоторой постоянной ошибки хcm. Более вероятным является случай, когда возмущающие воздействия при движении системы в этом режиме меняются во времени. Это объясняется тем, что при движении по гармоническому закону непрерывно будет меняться направление движения системы, и, следовательно, одновременно будет меняться направление действующих в системе сил. Этот случай является довольно сложным, и он может рассматриваться только в приложении к конкретным системам регулирования. Поэтому рассмотрим ошибку, определяемую только первым слагаемым выражения (4.15)
В линеаризованной системе при гармоническом управляющем воздействии (7.13) ошибка в установившемся режиме будет также меняться по гармоническому закону с частотой
Точность системы в синусном режиме может быть оценена по амплитуде ошибки, которая может быть найдена из (7.14) на основании подстановки p = jwK
Так как предполагается, что амплитуда ошибки значительно меньше амплитуды входного воздействия
где А(wK) – модуль частотной передаточной функции разомкнутой системы при w = wK. Последняя формула позволяет легко вычислять амплитуду ошибки в установившемся синусном режиме. Для этого необходимо располагать либо аналитическим выражением для передаточной функции разомкнутой системы, либо иметь экспериментально снятую амплитудную или амплитудно-фазовую частотную характеристику разомкнутой системы. Формула (7.17) широко используется также при расчете системы методом логарифмических амплитудных частотных характеристик (ЛАХ) В этом случае модуль А(wK) в децибелах, то есть
Рис. 7.1. ЛАХ разомкнутой САР Простота выражения (7.17) позволяет легко решить обратную задачу, то есть сформулировать требования к ЛАХ, которые необходимо выполнить, чтобы амплитуда ошибки в синусном режиме была не больше заданной. Для этого необходимо по заданному значению амплитуды управляющего воздействия Ymax и допустимой амплитуде ошибки хmax вычислить требуемое значение модуля частотной передаточной функции разомкнутой системы в децибелах
Это значение модуля необходимо отложить на логарифмической сетке при частоте управляющего воздействия wK. Полученная точка АK (рис. 7.1, б) обычно называется контрольной точкой для ЛАХ. Для того чтобы амплитуда ошибки в системе не превосходила допустимого значения хmax, ЛАХ должна проходить не ниже контрольной точки АK. Если ЛАХ пройдет через эту точку, то амплитуда ошибки будет равна допустимому значению. Если ЛАХ пройдет ниже точки АK, то ошибка будет больше допустимого значения.
|


 и т. д. Затем можно использовать изображения функции по Лапласу или Хевисайду – Карсону. В данном случае более просто применить изображения Хевисайда – Карсона, так как изображение постоянной величины равно ей самой, то есть
и т. д. Затем можно использовать изображения функции по Лапласу или Хевисайду – Карсону. В данном случае более просто применить изображения Хевисайда – Карсона, так как изображение постоянной величины равно ей самой, то есть  и т. д. Потом необходимо воспользоваться теоремой о предельном переходе и получить установившееся значение ошибки (статическую ошибку)
и т. д. Потом необходимо воспользоваться теоремой о предельном переходе и получить установившееся значение ошибки (статическую ошибку) . (7.2)
. (7.2) , (7.3)
, (7.3) – представляет собой второе слагаемое в выражении (7.2);
– представляет собой второе слагаемое в выражении (7.2);  – ошибка чувствительного элемента.
– ошибка чувствительного элемента. и при постоянных значениях возмущающих воздействий
и при постоянных значениях возмущающих воздействий 
 и т. д. Используя изображения Хевисайда – Карсона, имеем
и т. д. Используя изображения Хевисайда – Карсона, имеем  и т. д. Из общего выражения для ошибки (4.15) посредством теоремы о предельном переходе может быть найдена установившаяся ошибка в этом режиме
и т. д. Из общего выражения для ошибки (4.15) посредством теоремы о предельном переходе может быть найдена установившаяся ошибка в этом режиме . (7.4)
. (7.4) . (7.5)
. (7.5) . (7.6)
. (7.6) . (7.7)
. (7.7) . (7.8)
. (7.8) . Возмущающие воздействия принимаются постоянными, как и во втором типовом режиме.
. Возмущающие воздействия принимаются постоянными, как и во втором типовом режиме. . (7.9)
. (7.9) . (7.10)
. (7.10) . (7.11)
. (7.11)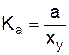 . (7.12)
. (7.12) . (7.13)
. (7.13) . (7.14)
. (7.14) . (7.15)
. (7.15) . (7.16)
. (7.16) , то, следовательно, модуль знаменателя (7.16) значительно больше единицы. Это позволяет с большой точностью выражение (7.16) заменить приближенным
, то, следовательно, модуль знаменателя (7.16) значительно больше единицы. Это позволяет с большой точностью выражение (7.16) заменить приближенным , (7.17)
, (7.17) , равен ординате ЛАХ при частоте wK (рис. 7.1, а).
, равен ординате ЛАХ при частоте wK (рис. 7.1, а).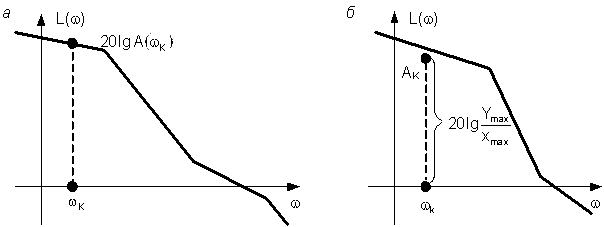
 . (7.18)
. (7.18)


