Дипольное, квадрупольное, мультипольное приближения.
Рассмотрим систему точечных зарядов
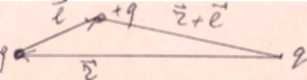
Рис. 19. Система зарядов Запишем потенциал поля в вакууме для системы точечных зарядов:
Где Если
Перед нами стоят две задачи: 1) доказать, что такое разложение возможно, 2) выяснить физический смысл членов разложения. Сначала займемся первой задачей. В курсе высшей математики изучалось разложение в ряд Тейлора:
Введем новые обозначения: вместо
Обобщим это разложение на функцию трех переменных
В этом разложении первый член называется нулевым приближением, так как добавки в нулевой степени, следующие три члена - линейное приближение с добавками в первой степени, затем девять членов - квадратичное приближение с добавками во второй степени. Теперь понятно, что следующие приближения содержат катастрофически нарастающее число членов /<3. Мы пока ограничимся квадратичным приближением. Применим написанное разложение (2.21) к (2.19). Введем обозначения: 9 так как Q зависит от ct у, -£ 9 J, добавки tty^-y*? так как в формуле ^ и v^, входит со знаком "минус". Р2~1£J Тогда получаем: Л Л ^ ^. \, Подставим это разложение в (2.19), сразу учитывая и разбивая на соответствующие члены приближения: „ Выражение (2.22) означает, что мы доказали возможность разложения уу.Й Теперь переходим ко второй задаче - выяснению физического смысла членов разложения (2.22). Найдем нулевое приближение: Итак, ' ^*23 ^ (2.23) формально совпадает с потенциалом точечного заряда. Поэтому ^0 называют приближением точечного заряда. В нулевом приближении произвольная система зарядов ведет себя как точечный заряд, если i*Oj т.е. система зарядов неэлектронейтральна. При этом суммарный заряд системы как будто находится в точке О, выбранной произвольно. Рассмотрим линейное приближение: В этом приближении система зарядов характеризуется вектором р=.Щ9еЪе, Производные ^ з /</л. D С учетом сделанных обозначений и введенных понятий получаем; где использован известный из векторного анализа результат Итак, Формально (2.24) совпадает с потенциалом поля диполя и называется поэтому дипольным приближением. В дипольном приближении система зарядов ведет себя как диполь с дипольным моментом j5*_z. 5 ^"zS 1, при этом Рассмотрим квадратичное приближение: ^4. / /;х В этом приближении система зарядов характеризуется более сложной величиной - моментом второго порядка, причем этот момент имеет 9 компонент. Квадрупольный момент можно записать в виде: Где (2.26) Из (2.26) видно, что … Поэтому тензор jfe.^ имеет 6 разных компонент. В конце темы мы покажем, Поскольку ^1ЛЫ(^Щ) — g$ Подставим в производную / Оставим временно член с — и запишем Аналогично получайся остальные производные. Обобщим эту формулу: ^,± \ ^ где - единичные тензор, равный с f / ± о о «-(^ X о Тогда окончательно: * 0 о ^ Счетом (2.25 и £2.27^ >j можно компактно записать: Г£_ называется квадрупольным приближением. Проведем тождественное преобразование, которое уменьшает число компонент тензора СЙ^уб до пяти независимых. Для этого сначала раскроем (2.28^), удваивая компоненты согласно свойству тензора: - Из выраяенриг в квадратных скобках вычтем выражение, тождественно равное lit*- з (£Г &) -u (2.30) В саном деле (й.ЗО^ можно преобразовать: v2ib2,?2- \ -%г~"7 /ез - (^ V С друге/ стороны можно ^й.ЗСЛболее понятно записать: + и сгруппируем ^Ч^/^ПГГ^сА тле? < В результате этого преобразования диагональные компоненты тензора мы простым соотношением, а именно: ^ Сто означает, что одна из диагональные компонент выражается через сую двух других, взятуЛсо знаком "минус", нацригер,: Поэтому остается вычислять только п..ть независимых компонент тензора. Примеры решения задач на квадрупольное приближение (см. Приложение Определен^ компонент кьадрупольноро момента играет большую роль в ядерной физике, так как по их значению мо::НО определить фор*гу лдра. Если ядро имеет сферически-симметричную форму, то все компонентыф^д Если есть отклонения от с^ергческо' 'тугетрпг, то некоторые компонент. ?оменты ' олее высокого порядка называется мультипольныыи. Соответс! но все ра^ло: ение -ля потенциала называется разложением по мультипол! моментам. Отметим, что уже начиная с квадрупольного приолигения разлс женив в.гекартовых координатах является неэффективным. Б самом деле i сначала пришлось записывать девять членов в, но оказалось, что только пять из них независгмы. ели проводить такое разложение в куб: ческом приближении - окту> ольном, то в декартовых координатах сначала пришлось бы записать <7 членов, тогда как анализ показывает, что то. ко 7 из них независимы. Имеется (олее рациональное выра ение jyiaf- в сидерических координ см^Согласно^. —запишем разло: ение для в форме: где)ft - Угол MeW £ и ^ ' -полином Ле.андра. Если ввести независимые сферические координаты - углы В и, Sf? и (индекс iC относится к заряду то п^теореме слдаенил полиномов Лежандра^ 3 запишем: (\f $ где Sm=jb приЛ1=.0, %h\ =-1 при fa>0. При этом полином Лежавд- ра определяется: ^ а присоединенные полином Лежандра: С учетом ^2.T'3j и (2*-%) потенциал^можно записать: Это и есть наиболее рациональное выражение доя разложения потенциала по мультипольным моментам. 3 самом деле, формула (2.35)сразу показывает лв явную зависимость потенциала от расстояния £. до точки наблюдения, мо- мент соответствующего порядка и число независимых членов в соответствую- щем приближении. ЦанримСр» см. Таблицу: Из приведенных примеров членов разложения видно, что на больших расстояниях основной вклад в потенциал дает *f0 - приближение точечного заряда, сто и есть оообнование возможности применения в электродинамике понятия точечного заряда к описанию произвольной системы зарядов, если, крнечно, ^ ^t^t'D > т.е. система зарядов неэлектронейтраиьнф.! § 12. Проводник в электростатическом поле Проводники имеют свободные, не связанные электрические заряды, т.е. свободные заряженные частицы. Под действием электростатического поля г исходит перемещение зарядов на поверхность проводника. Макроскопичеси описание дает следующие свойства проводника; i/ Так как в электростатике } -з-о, Х$ по закону Ома дл проводника при ^внутри проводника — 0 ♦ Вспомните клети Фарадея! 2/ Соответственно так же Ф а 0 и из 4-го уравнения Максвелла f~Tfrcttt$^, т.е. J»- °. ^ 3/ Поскольку 6" s ^^гл^^» но внутри ^"—^ t то^-А^Ус-О иУ=£о Весь проводник характеризуется одим значением потенциала ^. Поверхно проводника является первой эквипотенциальной поверхностью. 4/ Заряды располагаются на поверхности проводника, т.е. (Г^ t>. 5/ Из граничного условия СЗ^-^*и -Verff^t где 10<и^О внутри провод получаемк пУч^и &xn^*ftr£» т.е. внешняя напряженность вблизи поверхности тооводика направлен^ по нормали к поверхности проводика £jl =. ^£ fr. • При этом учтено, что касательная составляющая внешней напряженности б5т-=фогласно граничному условию Gxf— £ft~— о** Достаточно полное описание свойств проводника Q^cm. Тамм И.Е. * £J Для уединенного проводника заряд на его поверхности мокев быть запи рде - емкостный коэффициент или просто емкость. Если имеется несколько проводников, то заряд на одном из них, например где С*;* при <£^И - емкостныГ: коэффициент, ^ Ск-п при fc^fc - коэффициенты индукции /влияния /. Например, для двух проводников согласно CS.37) можно запивать: Если, f^^-p f например, для конденсатора, можно записат Пусть Yic-O. Складыяая an уравнения при Г,»0, получаем: 0=^ ^{С,г+Ся1_)ГКУА& при следует: Зьг--<?*4. Пусть теперь %.-0, складывая уравнения, получаем: 0— % •fiCju пщФ4фО следует, что = CjLf.Но следовател Cfitz&XL S С ^ где О - емкость конденсатора. С- мозг не найти из первого уравнения, например: Cf^t—^^J Тогда получае Емкость конденсатора, как известно из курса общей физики, зависит толь от свойств самого конденсатора. § 13. Диэлектрики в электростатическом поле План i. Диполь. Потенциал поля диполя. II. Поляризация диэлектрика. Вектор поляризации. III. Связь вектора поляризации с плотности) связанных зарядов. 1. Диэлектрики в отличие от проводников имеют связанные заряды. Форма но диэлектрик можно представить как совокупность^иполей - уже "готовы т.е. существующих и в отсутствии внешнего поля £"г09 или наведенных - ду:тированных внешним полем. В макгоскопическоГ электродинамике отвлека ся от этих деталей. Просто полагают, как мы уже ^ачале отметили, что диэлектрик состоит из диполей. Поэтому сначала вычислим потенциал поля диполя. Как известно, диполем называется система из двух разноименных, одинаковых по величине зарядов. Причем эти заряды расположен компакта т.е. достаточно близко друг к другу, на расстоянии £. При стом вектор £. направлен от — f к ftf.(см.Рис. 20.) Рис, 20 Диполь. К расчету Рис. 21. Диполь. К расчету дипольного момента р • потенциала ^. Согласно общему определению дипольный момент для диполя получаем: /так, для диполя дипольныР момент равен: ^ =zy<-. От выбора начала отсчета т. 0 %Р^>не зависит, так как т.О выбрана произвольно. Вычислим потениЗяал поля диполя в точке наблюдения Си при Согласно рис. 2i имеем для диполя: Сделаем приближения: так как Лег ц,, то предположим, что tZ.tfGr'i 9 в знаменателе Ъ-рТ*, ^ ^5. 9 в ^f^tj. - tcMJ- (• исJ| Тогда ^ j£c*£ Р^±,^ ^ Итак, потенциал поля диполя равен: ''огмула (^.39)в самом деле совпадает с формуле: (?.24^длл ^ из разд. жения для потенциала системы зарядов £см. §11)• ^ 11. Рассмотри!*поведение диолектрика во внешнем поле. При £Г* Я диэлект! полгризуется. ото значит, что объем Av диэлектрика приобретает дипол! ныР t/омент dj?» которы? можно записать: где г - вектор, характеризующий поляризацию диэлектрика и называем! вектором поляризации. Вектор поляризации- определяется как дипольный * мент единицы объема и равен: ^ *К;Х % - 6.4. Для дискретного распределения дипольных моментов ^ вектор поляризации определяется: ^ Щ; Я= v ксперименты показывают, что г* г-* _ где ^/ - коэффициент поляризации данного диэлектрика. 111. }'ы ввели два разных подхода к описанию диэлектрика: Ц с помогц»: связанных зарядов, которые можно охарактеризовать e-fTCVe объемной плотностью связанных зарядов^иу и поверхностной плотностью связан заргдов<^^/ с помощью вектора поляризации Р. Необходимо связать между собой эти введенные величины. Сначала предположим, что потенциал поля при наличии диэлектрика ново представить в виде: где Td - потенциал внешнего поля в вакууме, - потеншал поля за счет поляризации диэлектрика. При гтом (f6. ^ и аналогично согласно С другоР стороны выразим Yf<& через полгризациго Р. Для этого снача запишем потенциал от элемента объема dV как потенциал поли диполя с д польным гоменто?.' ctf ta затем введем вместо otf вектор поляризации С 2.40): Тогда для всего объема диэлектрика получаем: Преобразуем подинтегтальное выра^енре в у: ? *. ^ т > причем градиент берете1 по точке источника, лалее используем то: дество векторного анализа: J*foa)*№£+&-f"*'P.полагал 0.=Pj • Тогда тождество получим для /5 и ^: откуда; подинтегральное выра ение: Подставим в (^2.45) t сразу разбивая на два интеграла: Займемся вторым интегралом в (£.46J. lifc 1-й теореме Остроградского-Га- усса преобразуем: ^ /Г Л Но?то преобразование возможно, если внутри осъема у нет поверхносте разрыва. Рассмотрим разные случаи, I. Во всем пространстве, занятом полем, нет поверхносте'/ разрыва [Рц Тогда мо но применить ^2.47 \. Устремим поверхность ^ к ^ф, ох- ватывающее полное поле, • то ьгачг.т, что па S ВфлО,\ соответственно ~РzzO • ^то возможно, если заряды расположеня в конечное обласии п{ странства. В самом деле, разложение потенг нала системы зарядов показы- вает, что самое меменное убвание с расстоянием дает приближение точе* ного заряда ^ — • Соответственно, напряженность полк £*с*-91а*(\ Твевб^Л"^* ПрИ t~a?'t/> &о~>0 9 коне;шо учесть, что i леменз поверхности dSP&S>m Ц^5~ i^>^ "»о при • при : том учтено, ЧТО P^~V Eo"^*~l • Для других приближений будет солее быстрое убывание с увеличением рассто- яния. Поэтому можно положить: V Сравнивая И#4б^ с первым интегралом в Qj.46 J получаем: 2. Пусть внутри och>eua*V~ есть хотя бы одна поверхность разрыва $ на которой Рлу\- РчиФ 0 • На внешнее поверхности 5, окружающей гвйЬра ны# объем -у, разрыва нет, как и во всем остальном пространстве, заня- том полем. Зсе "неприятности" сосредоточены внутри данного осъема. Применим метод, которые успешно используется в электростатике и магнито- статике. Окру аем поверхность разрыва S/»yf* замкнутоГ поверхностью 3 \ на котогоС f>i непрерывна. При.-том поверхность S'.додходит достаточно слизко к £^ф>.(см. Рис 2с). Нормаль "Й к Sf*& направлена от 1-: ко 2-9. среде. Нормали Л1 и ~У{Ь направлены перпендикулярно элементам oi$<t г cfS^ 9 При этом Si и -С части поверхности ^/, кото- рые находятся в 1-й и 2-Р среде соответственно как указано на^Еис.^. РисД?ПЬвер; ности S; f^U, Тогда по 1-й теореме истроградского-Гаусса мояно записать: Первы* интеграл ty^S ^ Ф<*^°?$ "> ° / ушж в случае 1.,"Ак как все "неприятности") повторимся, содержатся во ром интеграле. < ян>чпии. 1»и»и^ип ъ*?]^—.нтутралг, Запишем отдельно второй интеграл: мы вря Iтом пренебрегли потоком через соковую поверхность, которая мала, так как £f достаточно 'лизко подходит к jy^. Их РиСлУвидно, что нор- маль параллельна нормали JJ, следовательно Рп* = п • Нормаль f)x аитипараллельна и» следовательно Ро^-Рд^* Устремляя Тогда десь мы опустили слово "разрыв", считая, что Л это и есть поверх- ность, на которой р1Иф Pxvy. Подставим этот результат в^2.4б): ° V v 5 ^ Сравнивая с VW~, получаем: Итак, мы нашли связь вектора поляризации с объемно^ре4^) и поверхност- но" (бс/л) плотностью связанных заргдов. Ос судим полученные результаты, i/ Согласно (j^.bO) pcti^^Oi если o/u)p^0 i т.е. елли поляризации неод- нородна, ото возмог.-но, если внешнеее поле неоднородно, если диэлектрик неоднороден, ^ если неоднородны? диэлектрик находится в неоднородном поле X/ Евли etu) ]$я-0 " однородный ди:лектрик в однородном поле, T0Jk(*£r о I Согласно ^•Sl^^ftntoHa поверхности 3 при p<Y% ^ рлИ 4/: ели нет скачка ри }, т.е. рщ-аЦ^ то Celtic о •то Феноменологическое описание, конечно, не раскрывает все многообразие диэлектриков и их поведение во внешнем поле, /"ля етого необходим более строги? подход - микроскопическое описание. § 14. Энергия в: лектростатике План I. энергия глектростатического поля. II. энергия зарядов, распределенных с объемной и поверхностно!1 плотностью ill. "нергия системы точечных зарядов в поле, 1У. энергия диполя в поле. #1* - нергия системы точечных зарядов: собственная энергия и энергия взаим действия. У*. Энергия диполь-дипольного взаимодействия. УII. Классический радиус электрона. I. По теореме Умова-Пойнтинга • нергия электромагнитного поля равна: Г /. Г£^$i Т§р})Л*' Я^Д*1 энергия лектростатического поля: Формула ^<!.5<!) означает, что энергия поля "размазана" по объему V" с объемной плотностью YVt-jl}rE£iJ?rO. Вея энергия поля согласно fe*b'd) всегда положительна. I тот вопрос обсу-дался в § 6. II. Получим энергию зарядов в поле. Для этого вводим ^иы^^ • Тог- да, подставив эту формулу в, полним: J -г* Qbtyuuflf преСразуем согласно то-.деству ^bjP^HJU? &Н4&*ЦА- согласно 4-му Уравнению: аксвелла, получим: %fl^^-с/^)-У^. одставив • то выражение в формулу для энергии и сразу разбивая ВДГдм интеграла, получаем: На ртом этапе 1нергия имеет вид:. Второй интеграл в ^«53)яВКМ| преобразовать по 1*1 теореме Остроградского Гаусса: р р Но так '".е, как И в 9 13, отметим, что применение; той теоремы возмож- но только в случае, если нет поверхностей разрыва подинтегральых функций* '-~-----• Т. v *^ *1 Рассмотрим два возможных случал. 1. Во всем пространстве, занятом полем, нет поверхностей разрываЯ)ли *f Тогда Ф Цф„ ~> /<<*Х„^ -*0, г'Де So -Поверхность, охватывающая полное поле, "ри этом WJbrrofS'** О при *£.-л^о. Сто возможно, если заряды находятся в конечной области пространства. Подробны?1 анализ аналогичных выражений мы уже проводили в § 13. Учтем этот результат и получим вместо выражение для энергии: 2 £»» одна поверхность взрыва нормальной составляющей вектора элект- рической индукции, на которой выполняете,- граничное условие Q.G7_p: 'АУЛ П — wi — ■ - Скалярный потенциал терпит разрыв при переходе через двойной электричес- кий слой (см, нарример, Й.Е. Таил \. Но двойные электричес- кие слои встречаются крайне редко, поэтому в дальнейшем всегда судем считать }f всюду непрерывным. Снова, как и в § 13, применим тот же рисунок 22. Тогда запишем: При этом с интегралом по внешней поверхности S можно поступить, как в 1-м случае, а именно: Поэтому остается интеграл по "внутренней" поверхности / t который приближенно можно записать на в виде суммы двух интегралов - по Sf и S%: Поскольку (0x4 = —$)fH» так как нормалв /?^и И параллельны, a — fdjfit так как нормали /?ь и (Г антипараллельны, то после устремления St ~>$/*лур ■ £t ^^^"bf» получаем: \У Spay,. Используем граничное условие (1.67 J и записываем: 1^ 4 ^ ', где снова опущено ■"слово" разрыв" для поверхности, на которой 0* и=МЭд> Подставим этот результат в (kJ.oS*) и получим: v-ijjw * (?.«) Фордгула /£.55^описываецшнергию зарядов, распределенных с объемно!':^ ^ и поверхностной (плотностью, в электростатическом поле, сто потенциаль- ная энергия заряженного вещества в поле. Вещество в ^.5^ представлен^ плотностями: арядов у к 0*» а поле - потенциалом V • Формула ласно ^2»661 энергией обладают только области пространства, в которых ill* ПереГдем теперь к нахождению энергии системы точечных зарядов в поле Объемная плотность заряда в самом простом случае / равномерное {ко- I V ' Дм точечного заряда f ведет себя "своеооразно", а именно: р ^ J о°; в точке, где находится заряд, так какТ=^^.5б) ) / О во всех остальных точках, так как в них^- о, Дирак преду* о ил использовать для описания $ дельта-функцш. Г/ 1 f °° > Х = ° Нормировка дельта-пункции - на единицу, т.е.. Ксли под знаком интеграла кроме или J^r-rf) находится непрерывная ХУД'™ /Л / 1 т0 ''нтбгр^лы вычисляются очень просто: лсть функции, которые ведут себя дельта-образно - если они иг/еот острый С учетом свойств дельта-функции Дурака можно ввести понятие объемной плот' где ^ характеризует положение заряда ty*, Проверим правильно ли мы ввели / согласно (2.60) Вычислим: Как и следовало ожидать, получился заряд все£сгстемы зарядов. При втои Итак, можно формально описывать систему точечных зарядов с помощью ОиЬеМНиУ! UAS/rnVVlB, n\j и —-------------- б/ Найдем энергию системы точечных зарядов в поле. Для этого использу- где использовано свойство С2.59) для трехмерного случая: Интегрирование ведется по всему пространству (2.61) Это потенпиальная энергия системы точечных зарядов в поле. При этом по- 1У. Найдем "полезную" формулу для энергии диполя во внешнем ncjiemif.l^?
Рис. 23. Диполь во внешнем поле Б точке ^ находится!. сточиик поля. 11а заряде -"-^ потенциал Разложим yfttfi) в ряд, считая: и подставим в энергию: ^ ~* ч Р!так, энергия диполя во внешнем поле: гта формула используется г- гиэике для описания поведения диэлектриков У. Найдем энергию диполь-дипольного взаимодействия, т.е. энергию двух При этом мы использовали тождество векторного анализа полагая tf=& и <f=(jg* t) Я (\>> * ^1 й^векторвог» анализа. Отдельно найдем: ^ХАМ(fi-Zj - -1* j £ * Ф- так как ft^Xfifo$i>fel я f не зависит от координат fXr^-l) точки наблюдения. Тогда напряженность поля диполя равна: Подставим ('г.бз) в формулу Г2.62 % получимrJ ^ 2. у= г* \г ' (а, Это и есть энергия диполь-дипольного взаимодействия. Тогда ■ В -нергия всех зарядов получится в виде: тих суммах можно выделить отдельно суммы при ^ и /*^f- if: rgjfW$&£*g ^Г^ц Ft*"?4 - собственная энергия системы точечных Второй член в /2.65) гавен конечному значению; iro энергия взаимодействия. Причем, МП W&»>0, то заряда от- В обгсем согласно энергия системы точечных зарядов бесконечна, но в ней есть конечное значение - энергия взаимодействия. УЛ. Классический радиус электрона. В современной теоретической физике существует проблема, связанная кая энергия шара, равномерно заряженного по объему.равна: С • J Если электрон - точечная частица, то его собственная энергия бесконечна, Если электрон - протяженная частица радиуса Q,, то его собственая Чтобы "примирить" электродинамику с СТО, в настоящее время предпола- 'де ^ - классический радиус электрона, равный Qt~*i ' СЛ4- § 15. Механические силы в электростатике. ~* Из определения вектора рлектркпеско? напрлтенкостк t слезет, что (J2.69) #Если заряд распределен по объему с плотностью Ф, то можно, вищоляя при- где j^pB - объемная плотность силы. В итоге, сила, действующая В случае поверхностного распределения зарядов с плотностью о дело Дл^ одного уединенного проводника возникает эффект растяжения его Для проводика, помещенного во внешнее поле, возникает аналогичный эф- Рис.25. Провод^во нешнем поле. £Г = С-Р^ б? внутри проводника Отсюда Тогда сила, действующая на фпеыент cl£: где "btut^ixi*1* tr5* при этом -$п*(= «мг * " ST0 поверхностнал^плот1 гость механическ* Наедем силу, де^ств^^уп на диполь в поле^. Согласно Рис.<;6 в точке, дите заряд т*-£ шрлмнрост c/^j, Находим результирутптую силу: Рис.^б. Диполь во внешнем поле. Подставим это разло- енне в силу г и получаем: где оператор fr-Pj = f*Vc ' Согласно сила действует на диполь в неоднородно?/; поле в стогону увелгченда (:. В од1:ородиом поле сила F равна нулю, но действует стороны. В ежим этот момент.1, р? 7 т-Zp У\л£7 - Момент N стремится повернуть диполь так, что(Лг/? совпадало с &.. Совместным действием момента N и силы объясняется притяжение лег-
|

 см. (рис. 19):
см. (рис. 19):

 - радиус-вектор заряда
- радиус-вектор заряда  ,
,  - радиус-вектор точки наблюдения, отсчитываемые от точки 0, выбранной произвольно внутри системы зарядов.
- радиус-вектор точки наблюдения, отсчитываемые от точки 0, выбранной произвольно внутри системы зарядов. , то
, то  можно разложить в ряд:
можно разложить в ряд:

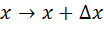 , где
, где  ; вместо
; вместо  . Тогда
. Тогда  и получим разложение по степеням малой добавки
и получим разложение по степеням малой добавки  :
:
 с малыми добавками
с малыми добавками  :
: