I. Метод обратной матрицы.В матричной форме система уравнений (4) имеет вид (3). Пусть матрица системы А (5) является невырожденной, т.е. существует обратная матрица А-1 (1). Умножив обе части этого уравнения слева на А-1, получаем решение системы (4) в матричной форме: Х= А-1В (6). Пример: Решить методом обратной матрицы систему уравнений:
Решение: 1) Обозначим А= 2) В матричной форме данная система имеет вид: АХ=В. Найдем определитель
= (-1)·(-1)1+2 Матрица не вырожденная и существует обратная матрица А-1. 3) Матрицу А-1 находим по формуле (1). Получим: А-1= 4) По формуле (6): Х= А-1В= 5) При подстановке полученных значений, получено верное тождество.
Контрольные вопросы по теме: 1. Что такое определитель системы линейных уравнений? ( ОК-1, ОК-2, ОК-11) 2. Какие системы называются совместными, несовместными, определёнными, неопределёнными, однородными, неоднородными? ( ОК-1, ОК-2, ОК-11) 3. Что такое решение системы? ( ОК-1, ОК-2, ОК-11) 4. Что такое матрица системы линейных уравнений? ( ОК-1, ОК-2, ОК-11) 5. Как записать систему линейных уравнений в матричной форме? ( ОК-1, ОК-2, ОК-11) 6. Как найти решение системы линейных уравнений в матричной форме ( ОК-1, ОК-2, ОК-11) Теоретические задания в тестовой форме ( ОК-1, ОК-2, ОК-11, ПК-1): 1. Если AY = C – матричное уравнение, в котором A, C, Y – матрицы, первые две из которых являются квадратными матрицами порядка n > 1, то укажите размер матрицы Y: n ×1; 1× n; m × n, m ≠ n; n × n; 2×2. 2. Решить матричное уравнение AY = C, где A и C – известные квадратные матрицы порядка n, означает найти матрицу AC; найти матрицу CA; найти такую матрицу B порядка n (если она существует), для которой AВ = C; найти матрицу А –1 или убедиться в том, что такой матрицы не существует; найти произведение матриц А –1· С, если матрица А –1 существует. 3. Пусть A, C, Y – квадратные матрицы порядка n; Yi, Ci – i -е столбцы матриц Y и C соответственно, i = 1, 2, …, n. Тогда уравнение AY = C и матрицу D= (A|C) называют соответствующими; задает n систем линейных уравнений A Yi = Ci, i = 1, 2, …, n, с единой матрицей коэффициентов А; задает (n + 1) матричных уравнений A Yi = Ci, i = 1, 2, …, n +1; имеет расширенную матрицу (A|C) размера n ×2 n; имеет расширенную матрицу (С|А) размера n ×2 n. 4. Строку расширенной матрицы (A|C), составленной для матричного уравнения AY = C, где A, Y, C – квадратные матрицы порядка n, будем называть противоречивой, если она состоит из одних нулей; первые ее n элементов – нули, а остальные отличны от нуля; первые ее n элементов отличны от нуля, а остальные – нули; первые ее n элементов – нули, а среди остальных элементов найдется хотя бы один ненулевой; в ней нет нулевых элементов. 5. Если расширенная матрица уравнения AY = C, где A, Y, C – квадратные матрицы порядка n, содержит противоречивую строку, то можно утверждать, что матричное уравнение имеет хотя бы одно решение; имеет, по крайней мере, одно решение; не имеет решений; имеет единственное решение; имеет бесконечно много решений. 6. Дано матричное уравнение AY = C с квадратными матрицами A, Y, C порядка n. Отметьте верные высказывания: если матрица А невырожденная, то уравнение AY = C можно решить методом Гаусса; если А – невырожденная матрица, то уравнение не имеет решений; если А – вырожденная, а С – невырожденная матрица, то уравнение не имеет решений; если А – невырожденная, а С – вырожденная матрица, то уравнение имеет бесконечно много решений; уравнение имеет единственное решение, если и только если матрица А – невырожденная. 7. Для матричного уравнения AY = C с квадратными матрицами A, Y, C одного и того же порядка укажите верные утверждения, описывающие взаимосвязь количества решений уравнения и свойств матриц А и С: уравнение имеет единственное решение, если матрицы А и С невырожденные; уравнение не имеет решений, если матрица А – вырожденная, а матрица С – невырожденная; уравнение не имеет решений, если матрица А – невырожденная, а матрица С – вырожденная; если решение уравнения единственно, то матрица А – вырожденная; если обе матрицы А и С – вырожденные, то уравнение может либо не иметь решений, либо иметь решение в зависимости от вида этих матриц. 8. Пусть A – квадратная матрица порядка n, Е – единичная матрица того же порядка. Матрицей, обратной для матрицы А, называется решение Y матричного уравнения: А+Y = E; А∙Y = E; Y·A = E; А+E = Y; А–Y = E. 9. Укажите матрицы, для которых обратные матрицы либо не существуют, либо вообще не определяются: вырожденные матрицы; невырожденные матрицы; квадратные матрицы, все элементы которых нулевые; прямоугольные матрицы размера m × n, где m ≠ n; матрицы, содержащие строку (столбец), состоящую из одних нулей. 10. Укажите верные высказывания: если матрица невырождена, то она имеет обратную; если матрица вырождена, то, в зависимости от ее вида, она может либо иметь, либо не иметь обратную матрицу; любая вырожденная матрица имеет обратную матрицу; матрица, имеющая обратную, невырожденная; матрица, имеющая обратную, является вырожденной. 11. Если А –1 – матрица, обратная для матрицы А, то справедливы следующие высказывания: обратной для матрицы А –1 является матрица А; матрицы А и А –1 являются взаимно обратными; А · А –1 = Е; А –1· А = Е; (А –1)–1 = А. 12. Среди следующих квадратных матриц укажите такую, которая обратна самой себе:
13. Среди следующих матриц укажите обратную матрицу для матрицы
14. Среди следующих матриц укажите обратную (если она существует) для матрицы
такой матрицы не существует;
15. Если A, В, Е – квадратные матрицы, для которых выполняется равенство A · В = Е, то отсюда следует, что А – невырожденная матрица; В – невырожденная матрица; А – обратная для В матрица; В – обратная для А матрица; выполняется равенство В · А = A · В.
16. Пусть A, Y, C – квадратные матрицы порядка n, причем А – невырожденная матрица. Тогда относительного матричного уравнения AY = C можно утверждать, что оно не имеет решения; оно имеет единственное решение; решением уравнения является матрица А –1 С; для решения уравнения можно использовать метод Гаусса; уравнение имеет более одного решения.
17. Если А – произвольная невырожденная матрица, то можно утверждать, что для нее существует обратная матрица А –1; для матрицы АТ существует обратная матрица (А – Т )–1; А –1 = (АТ)–1; (А –1) Т = А; (А –1) Т = (АТ)–1.
18. Пусть А, В – произвольные невырожденные матрицы одинакового порядка. Укажите верные утверждения: в зависимости от вида матриц А и В их произведение А·В может быть как вырожденной матрицей, так и невырожденной; для матрицы В·А существует обратная; для матрицы А·В существует обратная матрица; (А·В)–1 = А –1· В –1; (А·В)–1 = В –1· А –1. 19. Если А – произвольная невырожденная матрица, то справедливы следующие высказывания: АТ – невырожденная матрица; АТ может быть как вырожденной, так и невырожденной в зависимости от вида матрицы А; для матрицы А АТ существует обратная матрица; матрицы А и АТ имеют одну и ту же обратную матрицу; (А АТ)–1 = А –1 (А –1) Т. 20. Пусть A, Y, C – квадратные матрицы одного и того же порядка. В каком из следующих случаев матричное уравнение AY = C может иметь бесконечно много решений: А – невырожденная матрица; А и С – невырожденные матрицы; А – вырожденная, а С – невырожденная матрица; А и С – вырожденные матрицы; С – вырожденная, А – невырожденная матрица. Практические задания общие (ОК-1,ОК-2,ОК-11): Пример 1. Найти для матрицы
Решение. 1. Вычислим определитель матрицы:
2. Составим присоединенную матрицу, с этой целью вычислим алгебраические дополнения
3. Определим обратную матрицу, используя формулу (16):
4. Выполним проверку. Согласно определению произведение матриц А и А-1 должно дать единичную матрицу. Действительно,
2. Решить методом обратной матрицы систему:
Решение. A = Найдем A -1 № 3. Решить матричное уравнение: а) б)
A -1= Проверка: Подставим найденные значения переменных в систему:
Ответ: (2; 5; 0). № 4. Решите системы линейных уравнений матричным способом: а) г)
Индивидуальные задания (ОК-1,ОК-2,ОК-11) 1. Найти обратную матрицу для следующих матриц. 1. А = 4. А = 7. А =
2. Данную систему уравнений записать в матричной форме и затем решить с помощью обратной матрицы (матричным методом) 1.
4.
7. 10) 12)
14)
Рекомендуемое содержание отчета (для студента). 1. Название лабораторной работы 2. Цель и задачи исследований 3. Электронно-вычислительные средства для расчетов 4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию) 5. Выводы 6. Анализ и защита лабораторной работы производится по результатам представленного студенческой группой отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы) Преподаватель оценивает знание каждого студента. Литература
|

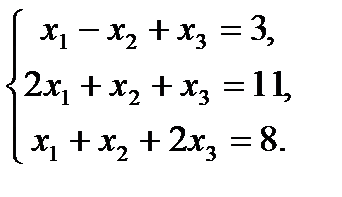
 ; Х=
; Х=  ; В=
; В= 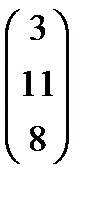 .
. :
: =
=  =
=  =
=  =
=  =
= =9-4=5
=9-4=5  0.
0.
 .
. =
=  =
=  , т.е. решение системы (4;2;1)
, т.е. решение системы (4;2;1) ;
; ;
; ;
; ;
; .
.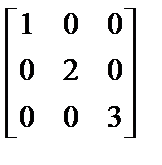 :
: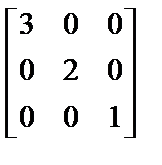 ;
; ;
; ;
; ;
; .
. :
: ;
; ;
; ;
; .
. обратную ей матрицу А-1.
обратную ей матрицу А-1.

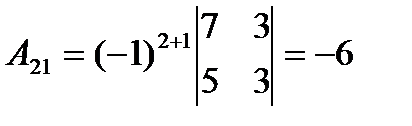

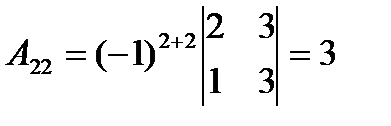






 или
или 


 , B =
, B =  , X =
, X =  .
.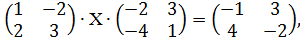
 ,
, . Теперь найдем X: X =
. Теперь найдем X: X =  . Итак,
. Итак, 


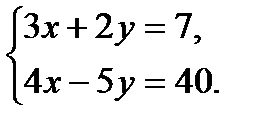 б)
б)  в)
в) 
 д)
д) 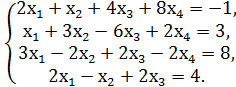
 2. А =
2. А =  3. А =
3. А = 
 5. А =
5. А =  6. А =
6. А = 
 8. А =
8. А =  9. А =
9. А = 
 2.
2.  3.
3. 
 5.
5.  6.
6. 
 8.
8. 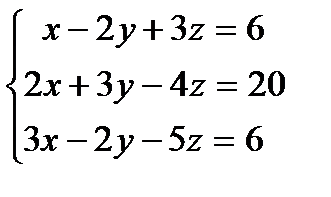 9.
9. 
 11)
11) 



