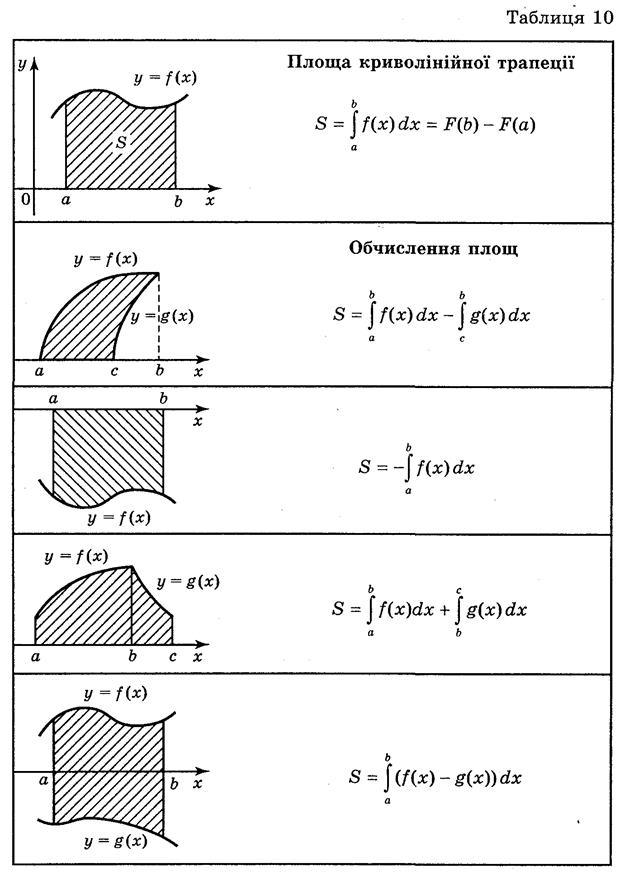
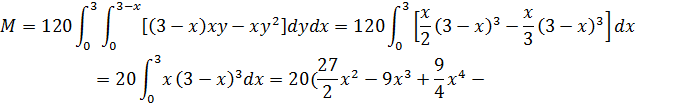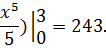З доведених теорем випливає, що 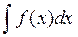 = F{x) + С, де F(x) — яка-небудь первісна для функції f(x) на даному проміжку, С — довільна стала (її називають сталою інтегрування).
= F{x) + С, де F(x) — яка-небудь первісна для функції f(x) на даному проміжку, С — довільна стала (її називають сталою інтегрування).
Таблиця первісних (невизначених інтегралів)

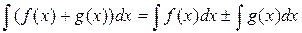
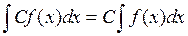
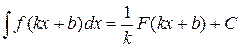
формула Ньютона-Лейбніца набирає вигляду:
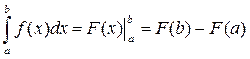
Із властивостей первісної і формули Ньютона-Лейбніца випливають основні властивості інтеграла.
1) Інтеграл суми (різниці) функцій дорівнює сумі (різниці) інтегралів:
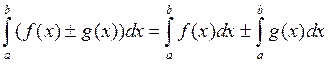 .
.
2) Постійний множник можна виносити за знак інтеграла:
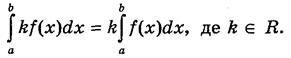
3) Якщо с є [а; b ], то 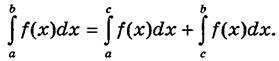

Поверхностный интеграл 1-го рода
Пусть  – кусочно-гладкая поверхность (то есть поверхность
– кусочно-гладкая поверхность (то есть поверхность  можно разбить на конечное число частей, на каждой из которых вектор нормали меняется непрерывно), расположенная в трехмерном пространстве. Рассмотрим произвольное разбиение поверхности
можно разбить на конечное число частей, на каждой из которых вектор нормали меняется непрерывно), расположенная в трехмерном пространстве. Рассмотрим произвольное разбиение поверхности  на частичные поверхности
на частичные поверхности  , площади которых равны
, площади которых равны  и пусть
и пусть 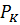 (
( – произвольные точки на поверхностях
– произвольные точки на поверхностях  . Тогда для скалярного поля
. Тогда для скалярного поля 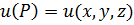 , определенного на
, определенного на  , можно составить интегральную сумму
, можно составить интегральную сумму 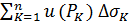 . Предел интегральных сумм при
. Предел интегральных сумм при  , если этот предел существует и не зависит от выбора разбиения поверхности
, если этот предел существует и не зависит от выбора разбиения поверхности  и выбора точек
и выбора точек 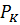 , называется поверхностным интегралом 1-го рода. Иными словами, поверхностный интеграл I-го рода определяется соотношением
, называется поверхностным интегралом 1-го рода. Иными словами, поверхностный интеграл I-го рода определяется соотношением
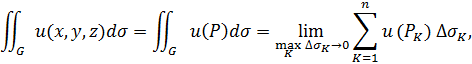
где  – дифференциал площади поверхности.
– дифференциал площади поверхности.
Если скалярное поле  непрерывно на поверхности
непрерывно на поверхности  , то поверхностный интеграл I-го рода существует.
, то поверхностный интеграл I-го рода существует.
Физический смысл этого интеграла зависит от характера данного скалярного поля: он может определять массу, распределенную по поверхности, электрический заряд, статический момент, момент инерции и т.д.
Приведем правило вычисления поверхностного интеграла 1-го рода.
Допустим сначала, что прямая, параллельная оси 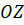 , пересекает поверхность
, пересекает поверхность  лишь в одной точке. Тогда эту поверхность можно задать уравнением
лишь в одной точке. Тогда эту поверхность можно задать уравнением  . Так как каждой точке из области
. Так как каждой точке из области  (проекция поверхности
(проекция поверхности  на
на  ) соответствует только одна точка на поверхности
) соответствует только одна точка на поверхности  , то вычисление поверхностного интеграла 1-го рода по поверхности
, то вычисление поверхностного интеграла 1-го рода по поверхности  сводится к вычислению двойного интеграла по области
сводится к вычислению двойного интеграла по области  . В самом деле, элемент
. В самом деле, элемент 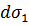 площади
площади  выражается в виде
выражается в виде
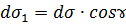 , где ɤ - острый угол, который нормаль к поверхности
, где ɤ - острый угол, который нормаль к поверхности  составляет с осью
составляет с осью 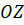 . Так как
. Так как 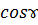 вычисляется по формуле
вычисляется по формуле
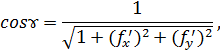
то для вычисления поверхностного интеграла 1-го рода в этом случае используется формула

Аналогично, если поверхность  однозначно проектируется на плоскость
однозначно проектируется на плоскость 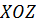 или
или  , то ее можно задать уравнением
, то ее можно задать уравнением  или уравнением
или уравнением  , и поэтому для вычисления интеграла I-го рода используются соответственно формулы:
, и поэтому для вычисления интеграла I-го рода используются соответственно формулы:
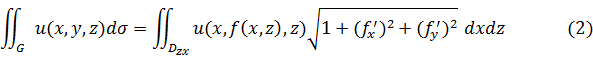
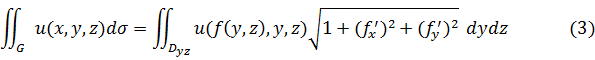
Наконец, если поверхность  нельзя однозначно спроектировать на координатные плоскости, то для вычисления поверхностного интеграла I-го рода, необходимо развить поверхность
нельзя однозначно спроектировать на координатные плоскости, то для вычисления поверхностного интеграла I-го рода, необходимо развить поверхность  на несколько частей, каждая из которых может быть однозначно спроектирована на одну из координатных плоскостей, а затем использовать одну из формул (1)-(3).
на несколько частей, каждая из которых может быть однозначно спроектирована на одну из координатных плоскостей, а затем использовать одну из формул (1)-(3).
 Пример 1. Найти момент инерции поверхности сегмента сферы с уравнением
Пример 1. Найти момент инерции поверхности сегмента сферы с уравнением 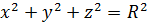 , отсекаемого плоскостью
, отсекаемого плоскостью  , относительно оси
, относительно оси  .
.
Решение.
Так как момент инерции элементарной площадки есть произведение квадрата расстояния от
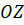
до этой площадки на площадь, то момент инерции всего сегмента

равен
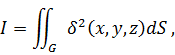
где 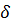 - расстояние от точки
- расстояние от точки  на поверхности сегмента до оси
на поверхности сегмента до оси  Ясно, что
Ясно, что 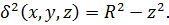
Кроме того, поверхность сферы задается уравнением 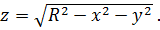 Поэтому
Поэтому
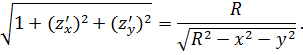
Отсюда, применяя формулу (1), находим
 где
где  – проекция поверхности интегрирования на плоскость
– проекция поверхности интегрирования на плоскость  (см. Рис.1). Переходя в последнем интеграле к полярным координатам, получим
(см. Рис.1). Переходя в последнем интеграле к полярным координатам, получим

где  .
.
Сделаем в последнем интеграле замену 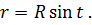
Тогда  , где
, где  . Поэтому
. Поэтому
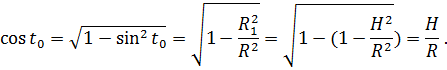
Следовательно,
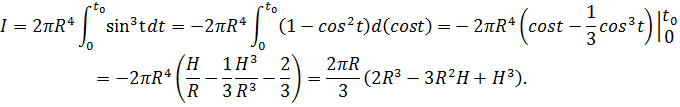
 Пример 2. Найти массу поверхности
Пример 2. Найти массу поверхности  , если известно, что плотность материала, из которого она состоит, равна
, если известно, что плотность материала, из которого она состоит, равна 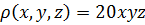 , а сама поверхность
, а сама поверхность  задана соотношениями:
задана соотношениями:
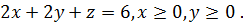
Решение. Масса определяется поверхностным интегралом I-го рода:

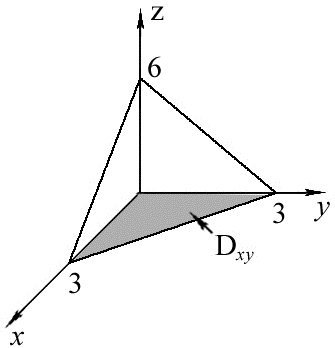
Так как поверхность  однозначно проектируется на плоскость
однозначно проектируется на плоскость  (см. Рис.2), то поверхностный интеграл
(см. Рис.2), то поверхностный интеграл 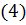 можно вычислить, используя формулу
можно вычислить, используя формулу  :
:
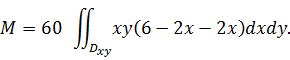
Здесь мы использовали соотношение  , в силу которого
, в силу которого 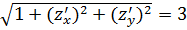 . Через
. Через  обозначена область
обозначена область 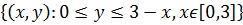 , лежащая в плоскости
, лежащая в плоскости  . Переходя в предыдущем равенстве к повторному интегралу, получаем
. Переходя в предыдущем равенстве к повторному интегралу, получаем
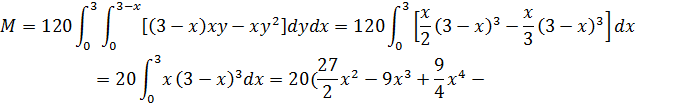
 до этой площадки на площадь, то момент инерции всего сегмента
до этой площадки на площадь, то момент инерции всего сегмента  равен
равен


 = F{x) + С, де F(x) — яка-небудь первісна для функції f(x) на даному проміжку, С — довільна стала (її називають сталою інтегрування).
= F{x) + С, де F(x) — яка-небудь первісна для функції f(x) на даному проміжку, С — довільна стала (її називають сталою інтегрування).
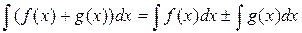
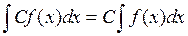
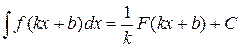
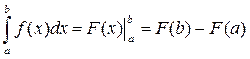
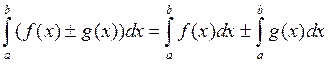 .
.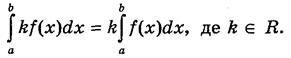
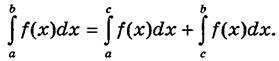


 , площади которых равны
, площади которых равны  и пусть
и пусть 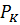 (
( – произвольные точки на поверхностях
– произвольные точки на поверхностях  . Тогда для скалярного поля
. Тогда для скалярного поля 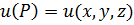 , определенного на
, определенного на 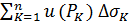 . Предел интегральных сумм при
. Предел интегральных сумм при  , если этот предел существует и не зависит от выбора разбиения поверхности
, если этот предел существует и не зависит от выбора разбиения поверхности 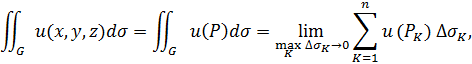
 – дифференциал площади поверхности.
– дифференциал площади поверхности. непрерывно на поверхности
непрерывно на поверхности  . Так как каждой точке из области
. Так как каждой точке из области  (проекция поверхности
(проекция поверхности  ) соответствует только одна точка на поверхности
) соответствует только одна точка на поверхности 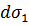 площади
площади 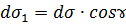 , где ɤ - острый угол, который нормаль к поверхности
, где ɤ - острый угол, который нормаль к поверхности 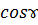 вычисляется по формуле
вычисляется по формуле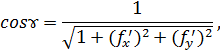

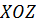 или
или  , то ее можно задать уравнением
, то ее можно задать уравнением  или уравнением
или уравнением  , и поэтому для вычисления интеграла I-го рода используются соответственно формулы:
, и поэтому для вычисления интеграла I-го рода используются соответственно формулы: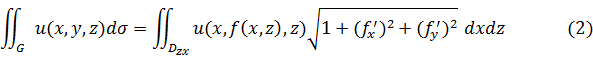
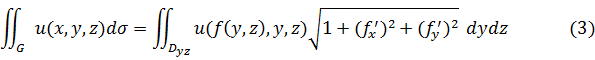
 Пример 1. Найти момент инерции поверхности сегмента сферы с уравнением
Пример 1. Найти момент инерции поверхности сегмента сферы с уравнением 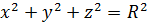 , отсекаемого плоскостью
, отсекаемого плоскостью  , относительно оси
, относительно оси 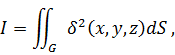
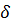 - расстояние от точки
- расстояние от точки  на поверхности сегмента до оси
на поверхности сегмента до оси  Ясно, что
Ясно, что 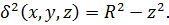
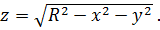 Поэтому
Поэтому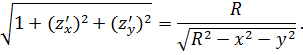
 где
где  – проекция поверхности интегрирования на плоскость
– проекция поверхности интегрирования на плоскость 
 .
.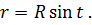
 , где
, где  . Поэтому
. Поэтому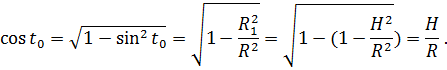
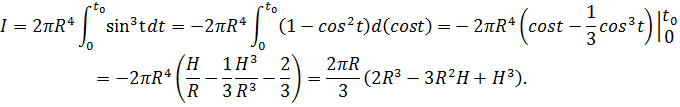
 Пример 2. Найти массу поверхности
Пример 2. Найти массу поверхности 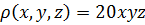 , а сама поверхность
, а сама поверхность 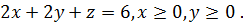
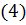 можно вычислить, используя формулу
можно вычислить, используя формулу  :
: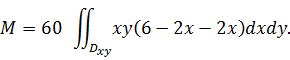
 , в силу которого
, в силу которого 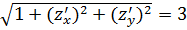 . Через
. Через 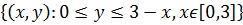 , лежащая в плоскости
, лежащая в плоскости