Анализ и обработка экспертных оценокПри проведении анализа собранных экспертных данных в соответствии с целями исследования и принятыми моделями необходимо представить информацию, полученную от экспертов в виде удобном для принятии решений (упорядочить объекты - варианты, показатели, факторы и т.п.), а также определить согласованность действий экспертов и достоверность экспертных оценок. Так, например, выявленные в процессе качественного анализа риски необходимо представить в порядке их важности (степени возможного их влияния на уровень потерь), или варианты снижения риска - в порядке их предпочтительности и т.п. Существует ряд методов упорядочения, каждый из которых имеет свои достоинства и недостатки, а также область эффективного применения. Наиболее распространенными из них являются: ранжирование, непосредственная оценка, последовательное сравнение, парное сравнение. Важным моментом экспертных процедур является оценка согласованности действий экспертов и достоверности экспертных оценок. Как отмечалось, существующие способы определения достоверности экспертных оценок основаны на предположении, что в случае согласованности действий экспертов достоверность оценок гарантируется. Наиболее часто для этих целей используют коэффициент конкордации (согласия), величина которого позволяет судить о степени согласованности мнений экспертов и, как следствие, достоверности их оценок. Коэффициент конкордации определяется из выражения: s2ф
s2max
где: s2ф - фактическая дисперсия суммарных (упорядоченных) оценок, данных экспертами; s2 max - дисперсия суммарных (упорядоченных) оценок, в случае, когда мнения экспертов полностью совпадают. Величина коэффициента конкордации может изменяться в пределах от 0 до 1. При W = 0 согласованности нет, т.е. связь между оценками различных экспертов отсутствует. При W = 1 - согласованность мнений экспертов полная. Для принятия решения об использовании полученных от экспертов оценок необходимо, чтобы коэффициент конкордации был больше заданного (нормативного) значения W н (W >W н). Можно принять W н = 0,5. Считается, что при W > 0,5 действия экспертов в большей степени согласованы, чем не согласованы. Определение коэффициента конкордации рассмотрим на следующем упрощенном примере. Пусть в процессе качественного анализа выявлены пять видов риска, которым может подвергаться проект в процессе его реализации. Перед экспертами стоит задача проранжировать эти риски (представить в порядке их важности) по степени возможного их влияния на уровень потерь. Результаты оценок этих рисков четырьмя экспертами представлены в табл. 5.1. Таблица 5.1 Определение рангов важности рисков
При полностью согласованном мнении экспертов каждый из них первому виду риска дал два балла, второму - один, третьему - четыре, четвертому - три, пятому - пять. В этом случае суммарный ранг важности рисков составил бы соответственно 8, 4, 16, 12 и 20 баллов. Известно, что среднее значение суммарной оценки для m объектов, назначаемых n экспертами, составляет ½ n (m +1) и в рассматриваемом примере среднее значение составляет - 12. Тогда: s2ф = (8-12)2 + (6-12)2 + (16-12)2 + (11-12)2 + (19-12)2 = 118 s2 max = (8-12)2 = (4-12)2 + (16-12)2 + (12-12)2 + (20-12)2 = 160
Таким образом, мнения экспертов можно считать в достаточной степени согласованными. В общем случае коэффициент конкордации определяется из выражения: m n 2 m 2 S { Sa ij - s2ô i=1 j=1 i=1
s2max
где: a ij - оценка, присваиваемая i -му объекту j- м экспертом; a i - суммарная оценка, полученная i - м объектом; m - количество оцениваемых объектов; n - количество экспертов. Используются также критерии, которые позволяют оценить вероятность того, что согласованность экспертов не явилась результатом случайных вариаций их мнений. Сущность методов упорядочения, а также оценки согласованности мнений экспертов и степени их достоверности достаточно полно изложены в [ 7; 14]. Если в соответствии с принятыми критериями мнения экспертов можно считать согласованными, то данные ими оценки принимаются и используются в процессе подготовки и реализации управленческих решений. Если полученные оценки нельзя считать достоверными, следует повторить опрос заново. Если и это не дает желаемых результатов, следует уточнить исходные данные и (или) изменить состав группы экспертов. Здесь следует отметить важную роль организаторов экспертизы, в задачи которых входят: - постановка проблемы; - определение целей и задач экспертизы, ее границ и основных этапов; - разработка процедур экспертизы, в наибольшей степени соответствующей характеру решаемой проблемы; - отбор экспертов, проверка их компетентности и формирование групп экспертов; - проведение опроса и согласование оценок; - формализация полученной информации, ее обработка, анализ и интерпретация. От правильной организации экспертизы в значительной степени зависит эффективность результатов, полученных посредством экспертных оценок, в т.ч. и достоверность этих оценок.
|

 W =,
W =, Риски
Эксперты
Риски
Эксперты
 W = = 0,7375
W = = 0,7375 n(m+1)} S{a i -
n(m+1)} S{a i - 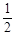 n (m+1)}
n (m+1)}

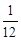 n2 m (m2-1)
n2 m (m2-1)  n2 m (m2-1)
n2 m (m2-1)



