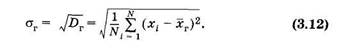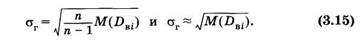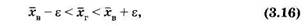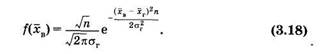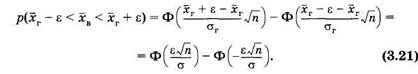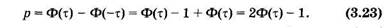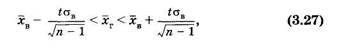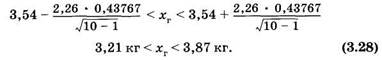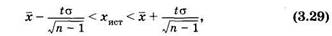Оценка параметров генеральной совокупности по ее выборкеПредположим, что генеральная совокупность является нормальным распределением (здесь вместо вероятности следует использовать относительную частоту). Нормальное распределение полностью определено математическим ожиданием (средним значением) и средним квадратическим отклонением. Поэтому если по выборке можно оценить, т. е. приближенно найти, эти параметры, то будет решена одна из задач математической статистики — определение параметров большого массива по исследованию его части. Как и для выборки, для генеральной совокупности можно определить генеральную среднюю хr — среднее арифметическое значение всех величин, составляющих эту совокупность. Учитывая большой объем этой совокупности, можно полагать, что генеральная средняя равна математическому ожиданию:
где X — общая запись случайной величины (значения изучаемого признака) генеральной совокупности. Рассеяние значений изучаемого признака генеральной совокупности от их генеральной средней оценивают генеральной дисперсией
(N — объем генеральной совокупности) или генеральным средним квадратическим отклонением
Точечная оценка. Предположим, что из генеральной совокупности производятся разные выборки; делают это так, чтобы вся генеральная совокупность сохранялась неизменной. Для определенности будем считать объемы этих выборок одинаковыми и равными п. Их выборочные средние х1, х2,..., xi.,... являются случайными величинами, которые распределены по нормальному закону (см. конец § 2.3), а их математическое ожидание равно математическому ожиданию генеральной совокупности, т. е.генеральной средней:
На практике иногда при достаточно большой выборке за генеральную среднюю приближенно принимают выборочную среднюю. Для дисперсий положение получается несколько иным. Математическое ожидание дисперсий различных выборок [M(Dвi)], составленных из генеральной совокупности, отличается от генеральной дисперсии:
При большом п получаем
Для генерального среднего квадратического отклонения соответственно из (3.14) и (3.14а) получаем:
На практике иногда при достаточно большой выборке выборочное среднее квадратическое отклонение приближенно принимают за генеральное среднее квадратическое отклонение. Так, если считать, что статистическое распределение (см. табл. 5) является выборкой из некоторой генеральной совокупности, то на основании (3.6) и (3.9) можно заключить, что для этой генеральной совокупности xr ≈ 3,468 кг и σг ≈ 0,3896 кг. Такого рода оценка параметров генеральной совокупности или каких-либо измерений определенными числами называется точечной оценкой. Интервальная оценка генеральной средней. Точечная оценка, особенно при малой выборке, может значительно отличаться от истинных параметров генеральной совокупности. Поэтому при небольшом объеме выборки пользуются интервальными оценками. В этом случае указывается интервал (доверительный интервал, или доверительные границы), в котором с определенной (доверительной) вероятностью р находится генеральная средняя.
Иначе говоря, р определяет вероятность, с которой осуществляются следующие неравенства: зуя функцию (3.18). Пределы интегрирования необходимо взять из выражения (3.19): где положительное число е характеризует точность оценки. Кроме доверительной вероятности используют «противоположное» понятие — уровень значимости
который выражает вероятность непопадания генеральной средней в доверительный интервал. Доверительную вероятность не следует выбирать слишком маленькой (не следует ее обесценивать). Наиболее часто р принимают равной 0,95; 0,99; 0,999. Чем больше р, тем шире интервал, т. е. тем больше е. Чтобы установить количественную связь между этими величинами, необходимо найти выражение для доверительной вероятности. Это можно сделать, используя (2.17), однако нужно понять, что при этом следует взять за функцию распределения вероятностей и какие принять пределы интегрирования. Рассмотрим этот вопрос. Итак, генеральная совокупность распределена по нормальному закону с математическим ожиданием (средним значением) хГ и дисперсией DT. Если из этой генеральной совокупности брать разные выборки с одинаковым объемом п, то можно для каждой выборки получить среднее значение хв. Эти средние значения сами являются случайными величинами. Их распределение, т. е. распределение средних значений разных выборок, полученных из одной генеральной совокупности, будет нормальным со средним значением, равным среднему значению генеральной совокупности хт, дисперсией — и средним квадратическим отклонением (см. конец § 2.2). Таким образом, хв уже выступает как случайная величина, для нее можно записать следующую функцию распределения вероятностей [см. (2.22)]:
Из (3.16) можно записать для хв следующие неравенства:
Вероятность того, что хв попадает в этот интервал (доверительную вероятность), можно найти по общей формуле нахождения р по х или т по р можно воспользоваться таол. ( или таблицей функции Ф (см. [2]).
Результаты интегрирования (3.20) найдем, используя функцию Ф (см. § 2.3). По формуле (2.25) получим
Обозначая
и учитывая (см. § 2.3), что Ф(-τ) = 1 - Ф(τ), получим из (3.21):
Таблица 7
Хотя неравенства (3.16) и (3.19) по существу идентичны, но для практических целей важнее запись (3.16), так как она позволяет решить главную задачу — при заданной доверительной вероятности и найденной выборочной средней найти доверительный интервал, в который попадает генеральная средняя. Запишем неравенство (3.16), подставив в него выражение εиз формулы (3.22):
Практически при нахождении доверительного интервала по формуле (3.24) берут выборочную среднюю некоторой конкретной выборки (объем п > 30), а вместо генеральной средней квадратичной используют выборочную среднюю квадратичную этой же выборки. Поясним это некоторым примером. Вновь обратимся к данным таблиц, считая их выборкой. Найдем доверительный интервал для генеральной средней, из которой эта выборка получена, считая доверительную вероятность равной р = 0,95. Из (3.23) для такой доверительной вероятности получаем: Ф(τ) = 0,975. В табл. 7 левый вертикальный столбец содержит значения с точностью до десятых долей, а верхняя горизонтальная строчка дает сотые доли т, поэтому для Ф(х) = 0,975 имеем х = 1,9 + 0,06 = = 1,96. Подставляя это значение τ, выборочную среднюю (3.6), выборочное среднее квадратическое отклонение (3.9) и объем выборки (п = 100) в выражение (3.24), или
Интервальная оценка генеральной средней при малой выборке. При достаточно большом объеме выборки можно сделать вполне надежные заключения о генеральной средней. Однако на практике часто имеют дело с выборками небольшого объема (п < 30). В этом случае в выражении доверительного интервала (3.16) точность оценки определяется по следующей формуле:
где t — параметр, называемый коэффициентом Стьюдента (его находят из распределения Стьюдента; оно здесь не рассматривается), который зависит не только от доверительной вероятности р, но и от объема выборки п. Коэффициент Стьюдента. Запишем неравенство (3.16), подставив в него выражение из формулы (3.26): 4п - 1
Поясним использование формулы (3.26) следующим примером. Предположим, что из генеральной совокупности, которую использовали при составлении выборки (см. табл. 5), взяли 10 случайных данных и получили следующее распределение (табл. 9): Таблица 9
Отсюда можно вычислить хв = 3,54 кг, DB = 0,19156 кг2 и св = 0,43767 кг. Задав доверительную вероятностью = 0,95, находим для объема выборки п — 10 параметр t = 2,26. Подставляя эти данные в (3.26), получаем для доверительного интервала [см. (3.27)]:
Полезно сопоставить соотношения, полученные для большой (3.25) и малой (3.28) выборок. Интервальная оценка истинного значения измеряемой величины. Интервальная оценка генеральной средней может быть использована для оценки истинного значения измеряемой величины. Пусть несколько раз измеряют одну и ту же физическую величину. При этом по разным случайным причинам, вообще говоря, получают разные значения: x1 x2, х3,.... Будем считать, что нет преобладающего влияния какого-либо фактора на эти измерения. Истинное значение измеряемой величины (xист) совершенно точно измерить невозможно хотя бы по причине несовершенства измерительных приборов. Однако можно дать интервальную оценку для этого значения. Если значения x1 x2, х3,... рассматривать как варианты выборки, а истинное значение измеряемой величины хист как аналог генеральной средней, то можно по описанным выше правилам найти доверительный интервал, в который с доверительной вероятностью р попадает истинное значение измеряемой величины. Применительно к малому числу измерений (п < 30) из (3.27) получим:
где х — среднее арифметическое значение из полученных измерений, а σ — соответствующее им среднее квадратическое отклонение, t — коэффициент Стьюдента. Более подробно и разносторонне оценка результатов измерений рассматривается в практикуме (см. [1]).
|