Построение сечения призмы плоскостью (приложение 1,2)Для построения сечения многогранника плоскостью необходимо либо найти точки встречи ребер многогранника с секущей плоскостью, либо построить линии пересечения его граней с этой плоскостью. В вариантах заданий ребра и грани многогранников занимают общее положение относительно плоскостей проекций π1 и π2 Секущая плоскость α, заданная различными способами, также занимает общее положение. Для решения задачи преобразуем чертеж таким образом, чтобы плоскость α заняла проецирующее положение. Используем для этого способ замены плоскостей проекций. x12 где π4┴ π1; π4┴α Находим точки встречи секущей плоскости α с ребрами призмы.
[AA'] ∩ α = 1; [A4 A'4] ∩ απ4 = 14; [BB'] ∩ α = 2; [B4 B'4] ∩ απ4 = 24; [CC'] ∩ α = 3; [C4 C'4] ∩ απ4 = 34;
По принадлежности определяем проекции этих точек на плоскости проекций π1 и π2. Треугольники 112131 и 122232 являются искомыми проекциями сечения призмы плоскостью.
|
x14 
,
x14┴h1, либо x14┴ απ1. На плоскости проекций π4 секущая плоскость α вырождается в прямую – след απ4 =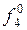 
.
