Построение сечения и развертки конуса вращения (приложение 5)В зависимости от положения секущей плоскости на поверхности конуса вращения может образовываться одна из кривых второго порядка – окружность, эллипс, парабола, гипербола. На примере, рассмотренном в приложении 5, плоскость α пересекает все образующие конуса под некоторым углом. В сечении получается эллипс. Для построения проекций сечения преобразуем чертеж так, чтобы секущая плоскость α стала проецирующей. Используем способ замены плоскостей проекций x12 π4┴π1; π4┴ α На плоскости π4 проекция сечения вырождается в отрезок прямой [14 54], лежащей на следе плоскости απ4. Большая ось эллипса - сечения - отрезок [15] лежит на линии ската плоскости α. Проведем вспомогательную горизонтально-проецирующую плоскость β через вершину конуса S перпендикулярно плоскости α: (β┴α) Такая плоскость пересечет поверхность конуса ω по двум образующим, а плоскость α - по линии ската: β∩ω = [S1]; [SV] β∩α = [MN]. На плоскости π4 в пересечении следа απ4 с очерковыми образующими [S4 14] и [S4V4] находим точки 14 и 15. Отрезок [14 54] Чтобы найти малую ось эллипса-сечения, проводим. горизонтальную плоскость γ через середину отрезка [15] – точку О (центр эллипса). Эта плоскость пересечет конус по окружности (параллели), а плоскость α – по горизонтали. В их пересечении найдем точки З и 8. Точки видимости 2 и 6 находим, проведя фронтальную плоскость σ через вершину конуса. Она пересечет его поверхность по очерковым образующим [SІІ] и [SVI], а плоскость α – по фронтали f1: σ∩ω = [SII]; [SVI] σ∩α = f1. В их пересечении находим точки 2 и 6:
f1∩ [SII] = 2, f1∩ [SVI] = 6.
С помощью параллели конуса (по принадлежности) на чертеже построены проекции промежуточных точек эллипса – 4 и 7. Точки 1,2,... 9 соединяем плавной кривой, используя лекало с учетом видимости. Натуральную величину сечения находим способом плоскопараллельного перемещения. Развертка боковой поверхности конуса вращения представляет собой круговой сектор, центральный угол которого равен
где r – радиус окружности основания конуса; Дуга окружности сектора равна длине окружности основания конуса. Чтобы перенести на развертку точки 1,2,..., 9 фигуры сечения, строим на развертке образующие, на которых лежат эти точки. Для этого на дуге сектора последовательно откладываем отрезки:
[I II] = [I1 II1]; [II III] = [II1 III1]
и т.д., полученные точки соединяем с вершиной сектора S. Откладываем на развертке отрезки образующих: [S4 14] = [S 1]; [S4 54] = [S5]; [S2 22] = [S 2]; [S2 62] = [S 6], так как дни проецируются без искажения на плоскостях π4 и π2 Точки 34 = 84 и 44 = 74 переносим на очерковую образующую [S4 I4], что соответствует вращению образующих, которым они принадлежат, вокруг оси конуса до положения, параллельного плоскости π4. Откладываем на развертке отрезки: [S4 [S4 и т.д. Точки 1,2,…,9 соединяем плавной кривой, используя лекало, достраиваем нижнее основание конуса и натуральную величину фигуры сечения – эллипс. ВОПРОСЫ ДЛЯ САМ0ПРОВЕРКИ 4.1. Чем задается призматическая поверхность, поверхность пирамиды? 4.2. Как рассекается призма плоскостью, параллельной боковым ребрам? 4.3. Что называется разверткой многогранника? Назовите способы её построения. 4.4. В чем заключается построение развертки призмы методом нормального сечения? 4.5. В каком случае можно построить развертку призмы методом раскатки? В чем он заключается? 4.6. В чем состоит построение способом триангуляции? 4.7. Как образуются конические и цилиндрические поверхности? 4.8. Какие линии получаются при пересечении цилиндрической поверхности плоскостью? 4.9. Как найти опорные точки сечения поверхности цилиндра плоскостью? 4.10. Как строится развертка боковой поверхности цилиндра вращения, наносятся на неё точки фигуры сечения? 4.11. Каково условие принадлежности точки поверхности? 4.12. Какие линии получаются при пересечении конической поверхности плоскостью? 4.13. Как используется метод вспомогательных секущих плоскостей для построения сечения конуса плоскостью общего положения? 4.14. Какие точки линии (фигуры) сечения поверхности вращения называются характерными, особыми, опорными? 4.15. Как построить развертку боковой поверхности конуса вращения и нанести на неё точки фигуры сечения?
|

 x14
x14 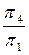 ,
, x14┴ h1.
x14┴ h1.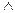 (β┴π1)
(β┴π1)  [15] является большой осью эллипса-сечения. Строим проекции линии ската [MN] на плоскостях π1 и π2 и по принадлежности находим проекции точек 1 и 5.
[15] является большой осью эллипса-сечения. Строим проекции линии ската [MN] на плоскостях π1 и π2 и по принадлежности находим проекции точек 1 и 5.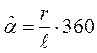 ,
, - образующая конуса.
- образующая конуса.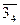 ] = [S 3],
] = [S 3], ] = [S 4]
] = [S 4]


