Собственные числа и собственные векторы линейного оператораНаиболее просто устроены матрицы диагонального вида Пусть дано линейное пространство Rn и действующий в нем линейный оператор A; в этом случае оператор A переводит Rn в себя, то есть A:Rn→ Rn. Определение. Ненулевой вектор Отметим некоторые свойства собственных чисел и собственных векторов. 1. Любая линейная комбинация собственных векторов 2. Собственные векторы 3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов. Итак, если имеется Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A. Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема. Теорема. Матрица линейного оператора A в базисе Правило отыскания собственных чисел и собственных векторов. Пусть дан вектор Уравнение (*) можно рассматривать как уравнение для отыскания Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений: где Система (1) имеет ненулевое решение, если ее определитель D равен нулю Получили уравнение для нахождения собственных чисел. Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду. Пусть λ1, λ2, …, λn - вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы. Пример 12. Линейный оператор A действует в R3 по закону Решение. Строим матрицу этого оператора: Составляем систему для определения координат собственных векторов: Составляем характеристическое уравнение и решаем его: λ1,2 = -1, λ3 = 3. Подставляя λ = -1 в систему, имеем: Так как Пусть x1 - свободное неизвестное, тогда Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: В пространстве R3 базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R3 составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем. Пример 13. Дана матрица 1. Доказать, что вектор 2. Найти базис, в котором матрица A имеет диагональный вид. Решение. 1. Если Вектор (1, 8, -1) - собственный вектор. Собственное число λ = -1. Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные. Собственные векторы ищем из системы: Характеристическое уравнение: (3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2 - 1) = 0 λ1 = -3, λ2 = 1, λ3 = -1. Найдем собственный вектор, отвечающий собственному числу λ = -3: Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x1 = x3 = 0. x2 здесь может быть любым, отличным от нуля, например, x2 = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим: Если λ = 1, то получаем систему Ранг матрицы равен двум. Последнее уравнение вычеркиваем. Пусть x3 - свободное неизвестное. Тогда x1 = -3x3, 4x2 = 10x1 - 6x3 = -30x3- 6x3, x2 = -9x3. Полагая x3 = 1, имеем (-3,-9,1) - собственный вектор, отвечающий собственному числу λ = 1. Проверка: Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R3. Таким образом, в базисе Не всякую матрицу линейного оператора A:Rn → Rn можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов. Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой Замечания. 1. Все собственные числа симметрической матрицы вещественны. 2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны. В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
|

 . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.
. Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует. называется собственным вектором оператора A, если оператор A переводит
называется собственным вектором оператора A, если оператор A переводит 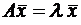 . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору
. Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору 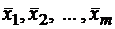 оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом. линейно независимых собственных векторов
линейно независимых собственных векторов  , соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы:
, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 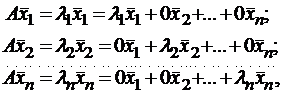 тогда
тогда  .
. (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса - собственные векторы оператора A.
(i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса - собственные векторы оператора A. , где x1, x2, …, xn - координаты вектора
, где x1, x2, …, xn - координаты вектора  и
и  , то есть
, то есть  . Это соотношение можно записать в матричной форме
. Это соотношение можно записать в матричной форме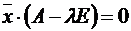 . (*)
. (*) , то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A - λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A - λE) = 0.
, то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A - λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A - λE) = 0. (1)
(1) - матрица линейного оператора.
- матрица линейного оператора. .
. , где x1, x2,.., xn - координаты вектора
, где x1, x2,.., xn - координаты вектора  ,
,  ,
, 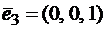 . Найти собственные числа и собственные векторы этого оператора.
. Найти собственные числа и собственные векторы этого оператора.
 .
.
 .
. или
или 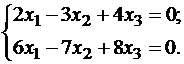
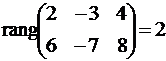 , то зависимых переменных два, а свободное одно.
, то зависимых переменных два, а свободное одно. Решаем эту систему любым способом и находим общее решение этой системы:
Решаем эту систему любым способом и находим общее решение этой системы:  Фундаментальная система решений состоит из одного решения, так как n - r = 3 - 2 = 1.
Фундаментальная система решений состоит из одного решения, так как n - r = 3 - 2 = 1.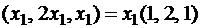 , где x1 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1:
, где x1 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: 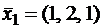 .
. .
. .
.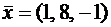 является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору. .
.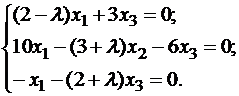
 ;
;
 .
.
 .
. ,
,  ,
, 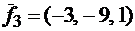 матрица A имеет вид:
матрица A имеет вид: .
. .
.


