Теоретико-множественный смысл разностиХороший пример, побуждающий нас стремиться к позитивным взаимоотношениям, мы находим в Библии: Одна из жен сынов пророческих с воплем говорила Елисею: раб твой, мой муж, умер. А ты знаешь, что раб твой боялся Господа. Теперь пришел заимодавец взять обоих детей моих в рабы себе. И сказал ей Елисей: что мне сделать тебе? скажи мне, что есть у тебя в доме? Она сказала: нет у рабы твоей ничего в доме, кроме сосуда с елеем. И сказал он: пойди попроси себе сосудов на стороне, у всех соседей твоих, сосудов порожних; набери не мало, и пойди, запри дверь за собою и за сыновьями твоими, и наливай во все эти сосуды; полные отставляй. И пошла от него, и заперла дверь за собой и за сыновьями своими. Они подавали ей, а она наливала. Когда наполнены были сосуды, она сказала сыну своему: подай мне еще сосуд. Он сказал ей: нет более сосудов. И остановилось масло. И пришла она, и пересказала человеку Божию. Он сказал: пойди, продай масло, и заплати долги твои; а что останется, тем будешь жить с сыновьями твоими. 4-я Царств 4:1-7 Внимательно рассмотрев этот отрывок, вы обнаружите следующее: • Вдова одного из пророков была связана с Елисеем дружескими взаимоотношениями. • Она добыла пустые сосуды благодаря своим хорошим взаимоотношениям с некоторыми соседями. • Ее чудо прекратилось, когда закончились сосуды, потому что у нее не было хороших взаимоотношений с другими соседями. Если бы у этой вдовы было больше друзей, у нее оказалось бы больше сосудов. Заметьте также, что: • негативные взаимоотношения принесли долги в ее жизнь; • негативные взаимоотношения чуть не отобрали у нее детей; • с мудростью стройте ваши взаимоотношения!
Теоретико-множественный смысл разности
Докажем это. Так как по условию В – собственное подмножество множества А, то их можно представить так, как на рис. 3.
Вычитание натуральных (целых неотрицательных) чисел определяется как операция, обратная сложению: а – b = с
Разность АВ на этом рисунке заштрихована. Видим, что множества В и АВ не пресекаются и их объединение равно А. Поэтому число элементов в множестве А можно найти по формуле n(A)=n(B) + n(AB), откуда по определению вычитания как операции, обратной сложению, получаем n(AB) = а – b.
Аналогичное истолкование получает вычитание нуля, а также вычитание а из а. Так как А
Разность а – b целых неотрицательных чисел существует тогда и только тогда, когда
Действие, при помощи которого находят разность а – b, называется вычитанием, число а – уменьшаемым, b – вычитаемым.
Используя определения, покажем, что 8 – 5 = 3. Пусть даны два множества такие, что n(A) = 8, n(B) = 5. И пусть множество В является подмножеством множества А. Например, А = { a, s, d, f, g, h, j, k }, B = { a, s, d, f, g }.
Найдем дополнение множества В до множества А: АВ = { h, j, k }. Получаем, что n(AB) = 3.
Следовательно, 8 – 5 = 3.
Представим условие задачи наглядно, изобразив каждое дерево, посаженное возле школы кружком (рис. 4). Среди них есть 3 березы – на рисунке выделим их штриховкой. Тогда остальные деревья – не заштрихованные кружки – и есть липы. Т. е. их столько, сколько будет из 7 вычесть 3, т. е. 4.
В задаче рассматриваются три множества: множество А всех деревьев, множество В – берез, которое является подмножеством А, и множество С лип – оно представляет собой дополнение множества В до А. В задаче требуется найти число элементов в этом дополнении.
По условию n(A) = 7, n(B) = 3 и B
Значит, n(C) = n(AB) = n(A)- n(B) = 7 – 3 = 4.
Следовательно, у школы росло 4 липы.
Рассматриваемый подход к сложению и вычитанию целых неотрицательных чисел позволяет истолковать с теоретико-множественных позиций различные правила.
Правило вычитания числа из суммы: чтобы вычесть число из суммы, достаточно вычесть это число из одного из слагаемых и к полученному результату прибавить другое слагаемое, т.е. при а
Выясним смысл данного правила: Пусть А, В, С – такие множества, что n(A)=a, n(B)=b и A
Правая часть равенства имеет вид:
Левая часть равенства имеет вид:
Правило вычитания суммы из числа: чтобы вычесть из числа сумму чисел, достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим, т.е. при условии, что a
Выясним смысл данного правила. Для данных множеств имеет место равенство
Тогда получим, что правая часть равенства имеет вид:
Следовательно (a + b) – c = (a– c) + b, приусловии, что а>c.
Выясним смысл данного правила: Пусть А, В, С - такие множества, что n(A) = a, n(B) = b, n(C) = c и С
Значит, А(ВС) =
Следовательно, n(А(ВС)) = n(
Правило вычитания числа из разности: чтобы из разности двух чисел вычесть третье число,достаточно из уменьшаемого вычесть сумму двух других чисел, т.е. (а – b) – c = a – (b + c). Доказывается аналогично правилу вычитания суммы из числа.
Пример. Какими способами можно найти разность: а) 15 – (5 + 6); б) (12 + 6) – 2?
Решение. а) Используем правило вычитания суммы из числа: 15 – (5 + 6) = (15 – 5) – 6 = 10 – 6 = 4.
Или 15 – (5 + 6) = (15 – 6) – 5 = 9 – 4 = 4.
Или 15 – (5 + 6) = 15 – 11= 4.
б) Используем правило вычитания числа из суммы: (12 + 6) – 2 = (12 – 2) + 6 = 10 + 6 = 16.
Или (12 + 6) – 2 = 12 + (6 – 2) = 12 + 4 = 16.
Или (12 + 6) – 2 = 18 – 2 = 16. В аксиоматической теории вычитание натуральных чисел определено как операция, обратная сложению: а – b = с Û ($ сÎN) b + с = а. Вычитание целых неотрицательных чисел определяется аналогично. Выясним, каков смысл разности таких чисел, если а = n(А), b = n(В).
Доказательство. Так как по условию В - собственное подмножество множества А, то с помощью кругов Эйлера их можно представить так, как на рисунке. Разность АВ на этом рисунке заштрихована. Видим, что множества В и АВ не пересекаются и их объединение равно А. Поэтому число элементов в множестве А можно найти формуле п(А) = n(В) +n(АВ), откуда, по определению вычитания как операции, обратной сложению, получаем, что n(АВ) =n(А) - n(В). Из рассмотренной теоремы следует, что с теоретико-множественных позиций разность натуральных чисел а и b представляет собой число элементов в дополнении множества В множества А, если а = n(А), b = n(В) и В Ì А: а - b = n(А) - n(В) = n (АВ), если В Ì А. Аналогичное истолкование получает вычитание нуля, а также вычитание а из а. Так как А =А, АА =0,то а-0=а и а-а=0. Взаимосвязь вычитания чисел и вычитания множеств позволяет обосновать выбор действия при решении текстовых задач. Выясним, например, почему следующая задача решается при помощи вычитания: «У школы росло 7 деревьев, из них 4 березы, остальные липы. Сколько лип росло у школы?» В задаче рассматриваются три множества: множество А всех деревьев; множество Вберез, оно является подмножеством множества А; и множество С лип - оно представляет собой дополнение множества В до А. В задаче требуется найти число элементов в этом дополнении. Так как по условию n(А) = 7, n(В) = 4 и В Ì; А, то n(С) = n(АВ) = = n(А) - n(В) = 7- 4. Разность 7 - 4 - это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи: 7 - 4=3. Следовательно, у школы росло 3 липы. Рассматриваемый подход к сложению и вычитанию целых неотрицательных чисел позволяет истолковать с теоретико-множественных позиций правила вычитания числа из суммы и суммы из числа. Выясним, например, теоретико-множественный смысл правила: «Если а, b, с - натуральные числа и а > с, то (а + b) - с = (а - с) + b».
Нетрудно доказать, что для данных множеств А, В и С имеет место равенство (А È В)С = (АС) È В. Но n((А ÈВ)С) = = n(А È В) - n(С) = (а + b) - с, а n((АС) ÈВ) = n(АС) + n(В) = (а - с) + b. И следовательно, (а + b) - с = (а - с) + b, если а > с. С теоретико-множественной позиции можно рассмотреть и смысл отношений «больше на» и «меньше на». В аксиоматической теории определение отношения «меньше на» («больше на») естественным образом вытекает из определения отношения «меньше». Действительно, из того, что а < b тогда и только тогда, когда существует такое натуральное число с, что а + с = b, имеем, что «а меньше b на с» или «b больше а на с». Если а = n(А), b = n(В) и установлено, что а < b, то, исходя из теоретико-множественного смысла отношения «меньше», в множестве В можно выделить собственное подмножество В1, равномощное множеству А, и непустое множество ВВ1. Если число элементов в множестве ВВ1 обозначить через с (с ¹ 0), то в множестве В будет столько же элементов, сколько их в А, и еще с элементов: n(В) = n(В) + n(ВВ1) или b = а + с, что означает, что «а меньше b на с» (или «больше а на с»). Итак, с теоретико-множественной точки зрения «а меньше b на с» (или «b больше а на с») означает, что если а = п (А), b = п(В), то в множестве В содержится столько элементов, сколько их в А, и еще с элементов. Так как с = n(ВВ1), где В1 Ì В, п(В) = b, п(В1) = а, то, по определению разности, с = а - b. Следовательно, чтобы узнать, на сколько одно число меньше или больше другого, надо из большего числа вычесть меньшее. Взаимосвязь действий над множествами с действиями над числами, теоретико-множественный смысл отношений «меньше на» и «больше на» позволяют обосновывать выбор действий при решении задач с этими отношениями. Рассмотрим, например, такую задачу: «На столе 5 чашек, а ложек на 2 больше. Сколько на столе ложек?» Легко видеть, что она решается при помощи сложения. Почему? В задаче речь идет о двух множествах: множестве чашек (А) и множестве ложек (В). Известно, что в первом множестве 5 элементов, т.е. n(А) = 5. Число элементов во втором множестве требуется найти при условии, что в нем на 2 элемента больше, чем в первом. Отношение «больше на 2» означает, что в множестве В элементов столько же, сколько их в А, и еще 2 элемента (См. рис.). А
В1 ВВ1 В Применимо к тем множествам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, и еще 2. Используя правило подсчета элементов в объединении непересекающихся множеств, получаем: n(В) = n(В1) + n(ВВ1) = 5+2. Так как 5 + 2 = 7, то получим ответ на вопрос задачи: на столе 7 ложек. Рассмотрим еще одну задачу: «На столе 5 чашек, а ложек на 2 меньше. Сколько на столе ложек?» Выясним, почему она решается при помощи вычитания. В задаче речь идет о двух множествах: множестве чашек (А) и множестве ложек (В). Известно, что в первом множестве 5 элементов, т.е. n(А) = 5. Число элементов во втором множестве надо найти при условии, что в нем на 2 элемента меньше, чем в первом. Отношение «меньше на 2» означает, что в множестве В элементов столько же, сколько их в А, но без двух (См. рис.). А
А1 АА1 В Применимо к тем множествам, о которых идет речь в задаче, это означает, что ложек на столе столько же, сколько чашек, но без двух. Таким образом, n(В) = n(А1) = = n(А) - n(А А1) = 5 - 2. Так как 5 - 2 = 3, то получим ответ на вопрос задачи: на столе 3 ложки.
Учебник Моро 1класс 1 часть: стр 80-85 Стр 105 1 класс 2 часть:стр 8 Более широко начинает рассматриваться вычитание:стр 29 Табличное вычетание:стр 80
2 класс 1 часть:стр 26 Стр 87 2 класс 2 часть: стр 3 (письменное вычесление) 3 класс 1 часть: стр 3 (продолжение) 3 класс 2 часть: стр 65
|

 Разностью целых неотрицательных чисел а и bназывается число элементов в дополнении множества В до множества А при условии, что n(A)=a, n(B)=b, B
Разностью целых неотрицательных чисел а и bназывается число элементов в дополнении множества В до множества А при условии, что n(A)=a, n(B)=b, B 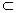 A, т.е. а - b = n(AB). Это обуславливается тем, что А=В
A, т.е. а - b = n(AB). Это обуславливается тем, что А=В  (АВ), т.е. n(A)=n(B) + n(AB).
(АВ), т.е. n(A)=n(B) + n(AB).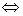 (
(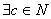 ) b + c = a.
) b + c = a.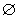 =А, АА=
=А, АА= 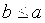 .
.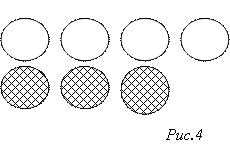 Взаимосвязь вычитания чисел и вычитания множеств позволяет обосновать выбор действия при решении текстовых задач.Выясним, почему следующая задача решается при помощи вычитания, и решите ее: «У школы росло 7 деревьев, из них 3 березы, остальные липы. Сколько лип росло у школы?»
Взаимосвязь вычитания чисел и вычитания множеств позволяет обосновать выбор действия при решении текстовых задач.Выясним, почему следующая задача решается при помощи вычитания, и решите ее: «У школы росло 7 деревьев, из них 3 березы, остальные липы. Сколько лип росло у школы?»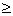 с имеем, что (a+b)-c=(a-c)+b; при b
с имеем, что (a+b)-c=(a-c)+b; при b 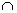 B=
B= 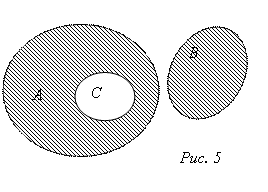 Нетрудно доказать с помощью кругов Эйлера, что для данных множеств имеет место равенство
Нетрудно доказать с помощью кругов Эйлера, что для данных множеств имеет место равенство 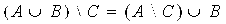 .
. .
.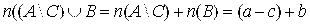 Следовательно (a + b) – c = (a– c) + b,приусловии, что а>c.
Следовательно (a + b) – c = (a– c) + b,приусловии, что а>c. .
.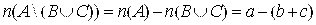 . Левая часть равенства имеет вид:
. Левая часть равенства имеет вид:  .
. Правило вычитания разности из числа: чтобы вычесть из числа а разность b – c, достаточно к данному числу прибавить вычитаемое с и из полученного результата вычесть уменьшаемое b; при a > b можно вычесть из числа а уменьшаемое b и к полученному результату прибавить вычитаемое с, т.е. а – (b – c) = (a + c) – b = (a – b) +c.
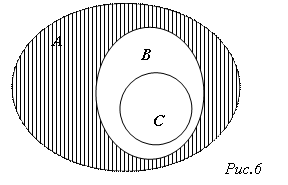
Правило вычитания разности из числа: чтобы вычесть из числа а разность b – c, достаточно к данному числу прибавить вычитаемое с и из полученного результата вычесть уменьшаемое b; при a > b можно вычесть из числа а уменьшаемое b и к полученному результату прибавить вычитаемое с, т.е. а – (b – c) = (a + c) – b = (a – b) +c.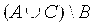 . На рисунке 5 множество А(ВС) изображено штриховкой. Легко убедиться в том, что множество
. На рисунке 5 множество А(ВС) изображено штриховкой. Легко убедиться в том, что множество 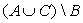 изобразится точно такой же областью.
изобразится точно такой же областью. .
.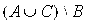 ) и а – (b – c) = (a + c) – b.
) и а – (b – c) = (a + c) – b. Теорема. Пусть А - конечное множество и В - его собственное подмножество. Тогда множество АВ тоже конечно, причем выполняется равенство п(АВ) = п(А) -п(В).
Теорема. Пусть А - конечное множество и В - его собственное подмножество. Тогда множество АВ тоже конечно, причем выполняется равенство п(АВ) = п(А) -п(В). Пусть А, В и С - такие множества, что n(А) = а, n(В) = b и А Ç В = Æ, С Ì А (См. рисунок).
Пусть А, В и С - такие множества, что n(А) = а, n(В) = b и А Ç В = Æ, С Ì А (См. рисунок).




