Шар (сфера) и плоскость
Текст задания: Задача 1. В прямом круговом конусе произведение высоты и радиуса основания равна 33. Найдите значения, которые может принимать радиус шара, описанного вокруг конуса. Задача 2. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра. Задача 3. Объём одного шара равен 16 π см3, а другого- 20 π см3. найдите радиус шара, объём которого равен сумме объёмов двух шаров. Задача 4. Площадь поверхности прямоугольного параллелепипеда равна площади поверхности шара. Найдите отношение объёмов параллелепипеда и шара, если ребра параллелепипеда, исходящие из одной вершины, относятся как 1:2:3. Задача 5. Площадь диагонального сечения куба, вписанного в шар, равна S. найдите объём шара. Задача 6. Диаметр шара радиуса 15 см разделён на 3 части, длины которых относятся как 2:3:5. через точки деления проведены плоскости, перпендикулярные диаметру. Найдите объём образовавшегося шарового слоя. Задача 7. Три сферы попарно касаются(внешним образом), а также касаются плоскости альфа в вершинах прямоугольного треугольника. Найдите сумму радиусов сфер, если катеты указанного треугольника равны 10см и 20см. Задача 8. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60 градусов. Найдите отношения объемов шара и конуса. Задача 9. Радиусы основания шарового слоя 3 и 4 см, а радиус шара-5см. Найти объем слоя, если его основания расположены по разные стороны от центра шара. Задача 10. Объем шара 400Пи,на радиусе как на диаметре построен другой шар. Найти объем малого шара. Контрольные вопросы: [2, стр. 333(12 – 21), 360(4 – 6, 9)] Раздел 8. Координаты и векторы Самостоятельная работа № 19 Тема: Нахождение расстояния между точками Цель: закрепить знания и умения студентов по освоению темы методом решения задач. Теоритическое обоснование: Прямая: Общее уравнение прямой:
Ах + Ву + С = 0,
где А и В не равны нулю одновременно. Коэффициенты А и В являются координатами нормального вектора прямой (т.е. вектора, перпендикулярного прямой). При А = 0 прямая параллельна оси ОХ, при В = 0 прямая параллельна оси ОY. При В
Уравнение прямой, проходящей через точку (х 0 , у 0) и не параллельной оси OY, имеет вид:
у – у 0 = m (x – х 0),
где m – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ. При А
где a = – C / A, b = – C / B. Эта прямая проходит через точки (a, 0) и (0, b), т.е. отсекает на осях координат отрезки длиной a и b. Уравнение прямой, проходящей через две различные точки (х 1, у 1) и (х 2, у 2):
Параметрическое уравнение прямой, проходящей через точку (х 0 , у 0) и параллельной направляющему вектору прямой (a, b):
Условие параллельности прямых:
1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AE – BD = 0,
2) для прямых у = m x+ k и у = p x+ q: m = p.
Условие перпендикулярности прямых:
1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AD + BE = 0,
2) для прямых у = m x+ k и у = p x+ q: m p = – 1. Расстояние между двумя точками (x 1, y 1) и(x 2, y 2):
Расстояние от точки (х 0 , у 0) до прямой Ах+ Ву+ С = 0:
Расстояние между параллельными прямыми Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0:
Угол
Текст задания: 1. Найти расстояние от начала координат до прямой x + y - 2 = 0. 2. Найти расстояние от точки (2, 5) до прямой 6 x + 8 y - 5 = 0. 3. Найти расстояние между двумя параллельными прямыми 3 x + 4 y - 12 = 0 и 3 x + 4 y + 13 = 0. 4. Найти уравнение прямой, проходящей через точку (-4, 3) и удаленной от начала координат на расстояние 5 единиц. 5. Через точку (-1, 2) провести прямую, расстояние от которой до точки (3, -1) равно 2 единицы. 6. Через точку M 1(1, 2) провести прямую, расстояния до которой от точек M 2(2, 3) и M 3(4, -5) были бы равны. 7. Дана прямая 4 x + 3 y + 1 = 0. Найти уравнение прямой, параллельной данной и отстоящей от нее на 3 единицы. Контрольные вопросы: [2, стр. 286(1 – 10, 14 – 16)] Самостоятельная работа № 20 Тема: Действия над векторами Цель: закрепить знания и умения студентов по освоению темы методом решения задач. Теоритическое обоснование:
|


 Всякое сечение шара (сферы) плоскостью есть круг (окружность)
Всякое сечение шара (сферы) плоскостью есть круг (окружность)






 0 получаем уравнение прямой с угловым коэффициентом:
0 получаем уравнение прямой с угловым коэффициентом: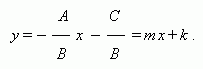


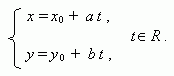



 между прямыми:
между прямыми:



